基于自发辐射相干效应的可调光子带隙反射率的提高方法∗
2018-12-14杨柳郜中星2薛冰张勇刚蔡永茂
杨柳 郜中星2)† 薛冰 张勇刚 蔡永茂
1)(哈尔滨工程大学自动化学院,哈尔滨 150001)
2)(哈尔滨工程大学理学院,哈尔滨 150001)
3)(东北电力大学理学院,吉林 132012)
(2018年7月17日收到;2018年8月28日收到修改稿)
1 引 言
在过去的二十年里,电磁诱导透明(electromagnetically induced transparency,EIT)效应备受关注并产生了许多有趣的应用,例如慢光效应、量子存储和非线性增强[1−7]等.起初,人们对光子带隙的研究仅局限于光子晶体中.折射率随着介质长度呈现周期性变化,由于入射场的布拉格散射,导致某些特定频率的光在传播过程中不能够透过介质,这些带隙被描述为光子带隙(photonic band gap,PBG)[8].众所周知,光子晶体一旦形成其周期性结构就固定了,获得的带隙宽度、位置及反射率等也就固定了,因此传统光子晶体的PBG是不可调节的[9].21世纪初,基于量子干涉的动力学可调PBG的问世弥补了这一缺陷.前期,人们利用空间周期性传播的驻波耦合场,使介质的折射率呈周期变化形成光子禁带[10−14].近期,在EIT条件下,利用囚禁在光学晶格中的冷原子来产生可调PBG也已取得了惊人的进步[15].这两种方案本质上均是通过使折射率呈现周期性状态来产生光子带隙结构,并且动力学可调.不同的是,后者将冷原子俘获在一维光晶格中,利用原子在光晶格中周期性分布的特性,在行波场的驱动下产生光子禁带.不同于驻波场驱动的Λ型原子系统的PBG,冷原子光晶格系统中会产生两个带隙,并且带隙的特性不仅受控制场的调制,而且还受探测场和光晶格之间的夹角及晶格波长的影响[16].随后,Schilke等[17]还对对布拉格反射进行了实验研究,并报道了透射和反射的测试光谱.
自发辐射相干(spontaneously generated co-herence,SGC)是指原子从两个足够靠近的上能级(或同一上能级)向同一个基态能级(或两个足够靠近的下能级)自发弛豫时由真空辐射场在两个辐射通道间感生出来的原子干涉效应[18−20].该现象能够引起许多有趣的现象,例如无反转激光、增强非线性Kerr效应[21−23]等.一直以来,人们都致力于提高PBG的反射率,反射率越高就越利于提高光路由和光隔离器等的效率[24−27].一般而言,在无增益介质中,由于EIT效应,PBG的反射率可以不断接近1,但由于光信号在传播过程中介质以及其他器件或结点带来的损耗会降低光信号的强度.因此本文提出一种可以通过考虑SGC效应来提高PBG反射率的方法,并且选取适当的条件参数,反射率甚至能够高于1.该方法可以补偿传播过程中的不必要损耗,提高光信号的传输效率.
本文展示的一维PBG由囚禁在一维光晶格中的冷原子产生,并且该系统可以产生两个PBGs.考虑基态两能级为超精细结构的三能级Λ型原子系统,自发辐射效应会使两个PBGs产生高的反射率.我们还进一步观察了探测场的增益-吸收情况来探究PBG反射率提高的原因.另外,对PBG的反射率与两个偶极矩之间的夹角和非相干驱动场强度等参数之间的关系也进行了详细讨论.
2 理论模型
考虑一个简单的三能级Λ型原子系统,如图1所示,其中频率为ωp(Ep)和ωc(Ec)分别作用在偶极允许跃迁的两个探测场上.相应的激光场拉比频率Ωp=Ep·d13/(2~),Ωc=Ec·d12/(2~),其中dij是跃迁的电偶极矩.同时,探测场和耦合场的单光子失谐被定义为∆p= ω31−ωp,∆c= ω21−ωc.值得注意的是,所选的三能级原子结构的两个基态为超精细结构能级,因此两个自发辐射跃迁通道Γ31和Γ21会产生相干,即SGC效应.一维光晶格是由波长为λlatt的红失谐激光反射形成的,大量原子俘获在其中.
在相互作用图象下,通过电偶极近似和旋转波近似,我们可求得光波场与原子系统的相互作用哈密顿H如下:


图1 三能级Λ型原子系统 (a)三能级原子系统与弱探测场Ep和强耦合场Ec相互作用;(b)相应的两电偶极距d13和d12之间夹角为θ;(c)冷原子被束缚在周期为alatt=λlatt/2的一维光晶格中Fig.1 .Three-level Λ-type atomic system:(a)A threelevel atomic system interacting with a probe f i eld Ep and a coupling f i eld Ec;(b)the angel between the relevant dipole moments d13and d12is θ;(c)atoms are trapped in an optical lattice formed by a retroref l ecting laser beam of wavelength alatt=λlatt/2.
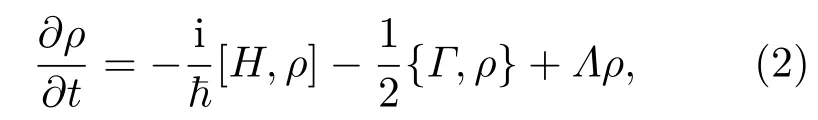
其中等式右侧第一项代表源于相干驱动场的可逆过程,第二项和第三项分别代表源于自发辐射和非相干驱动场的不可逆过程.将H代入(2)式,我们可得到如下的密度矩阵方程组:

(3)式满足粒子数守恒和共轭条件,即ρ11+ρ22+ρ33=1和代表能级和能级之间的相干弛豫速率,代表源于自发辐射通道和之间的交叉耦合的量子干涉效应,即SGC效应.耦合场和探测场的初始相位分别为ϕc和ϕp,Ωc= Ωc0exp(iϕc)和Ωp= Ωp0exp(iϕp),其中Ωc0和Ωp0为实数,ηΦ= η eiΦ,Φ = ϕp− ϕc表示两相干场的相对相位.注意,只有当能级|2〉和|3〉的间隔足够小时,我们才必须考虑SGC效应,才有η=1,否则η=0.对于如图1(a)所示的原子模型,我们有
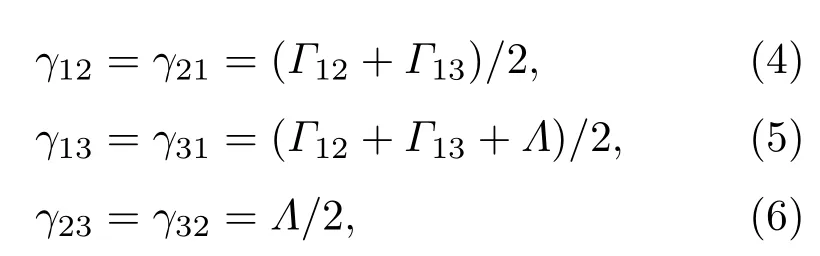
Λ表示非相干驱动场抽运速率.于是,我们通过稳态下(∂tρij=0)求解(3)式来获得探测场的极化率χp(z),即

如图1(c)中所示,冷87Rb原子被囚禁于一个驻波偶极阱中,该偶极阱利用一个波长为λlatt的红失谐回反射激光形成. 势阱的深度Ulatt与样品温度T0有关,二者之比为一个常系数ξ=Ulatt/(kBT0)(kB表示玻尔兹曼常数).用来形成晶格的激光波长必须满足λlatt>λ31来形成偶极阱.这意味着布拉格条件可以通过一个探测场和晶格之间的非零传输角α来满足,而且α需要足够小使得探测场能够与整个晶格长度相互作用.通过几何布拉格条件λ0= λ31/cosα,我们可以定义∆λlatt= λlatt−λ0.每个晶格周期原子密度分布满足,沿z方向的均方根谱宽为表示沿z方向上第i个周期的中心位置且alatt=L/n表示每个周期的长度,N0表示平均原子密度,则在这个原子介质中,我们将利用传输矩阵理论.首先,构建第j个周期的传输矩阵Mj,该周期长度可以被分成很多层,例如厚度δz(≪alatt)均匀的100层结构.每个周期的传输矩阵Mj是周期内每层传输矩阵mj(zl)的乘积,mj(zl)的系数由菲涅耳系数给出[28],并与反射rj和透射系数tj有关,即

于是Mj=mj(z1)···mj(zl)···mj(z100). 第二,由于每个偶极阱内原子密度是相同的,我们可以容易地获得整个原子介质长度L=nalatt的传输矩阵M=,如图1(c)所示.并且,探测场的反射率和透射率可以通过(9)式计算,

其中M(ij)是整个介质传输矩阵M的矩阵元.
3 数值结果及分析
在图1(c)所示的一维光晶格系统中,不考虑SGC效应(η=0),探测场会在EIT窗口内产生两个带隙PBG1和PBG2,其理论反射率均在80%左右,如图2(a)中黑色虚线.本文同样采用三能级系统,考虑基态|2〉和|3〉为超精细结构,即SGC效应(η=1)对PBG效应带来的变化.我们先对PBG2进行探究,发现该系统考虑SGC效应后,探测场反射率明显提高,PBG2的反射率甚至高达1.06,如图2(a)中红色实线.由于探测场的增益-吸收曲线正比于Im(ρ31),Im(ρ31)大于0则表示探测场处于增益状态,Im(ρ31)小于0则表示探测场处于被吸收状态.图2(b)进一步给出探测场的增益-吸收曲线,并且为了方便观察,插图中我们将反射率大于1的失谐区域进行放大.可以清楚地看到,在PBG2反射率大于1的区域,Im(ρ31)的值大于0,即出现探测场增益现象.这说明带隙出现大于1的情况是由于探测场增益导致的,这也解释了反射率提高的能量来源.但是否探测场增益就一定会导致反射率大于1的情况将在下文中讨论.接下来,我们介绍如何操控PBG2平台的反射率.
为了探究如何操控PBG2的反射率,我们观察了非相干驱动场抽运速率Λ分别为0.07Γ,0.08Γ和0.09Γ以及偶极矩θ分别为0,π/6和π/4情况下的反射率和增益-吸收特性随探测场失谐演化的情况.从图3(a)和图3(b)可以看出,在一定范围内,随着Λ的增加,PBG的反射率由0.97增加到1.08,并且探测场的极化率也不断增加.从图3(c)和图3(d)可以看出,随着SGC效应(cosθ)的增强,PBG的反射率由0.94增加到1.05,其探测场的极化率也不断增加.这说明对于PBG2,SGC效应的加强(Λ和cosθ增加),是反射率不断提高的有效方法.也进一步证明,探测场极化率的增加是使系统反射率提高的主要原因.并且当反射率出现大于1的情况时,探测场均会相应地出现增益.

图2 η=0(黑色虚线)和η=1(红色实线)情况下探测场的反射率和探测场的增益-吸收与失谐∆p/Γ的关系,其中Λ =0.06Γ,Φ =0,θ=0,Ωc0=20Ωp0= Γ,∆c=0,Γ32=0.001 MHz,Γ12= Γ13= Γ =6 MHz,λlatt=781.00 nm,∆λlatt=0.25 nm,λ31=780.02 nm,N0=7.0×1010cm−3,L=3.0 mm (a)反射率与失谐的关系;(b)增益-吸收与失谐的关系Fig.2 .The ref l ectivities and the gain or loss of the probe f i eld versus the detuning ∆p/Γ as η =0(black dashed line)and η =1(red solid line),where Λ =0.06Γ,Φ =0,θ =0,Ωc0=20Ωp0= Γ,∆c=0,Γ32=0.001 MHz,Γ12= Γ13= Γ =6 MHz,λlatt=781.00 nm,∆λlatt=0.25 nm,λ31=780.02 nm,N0=7.0× 1010cm−3,L=3.0 mm:(a)The ref l ectivities versus the detuning;(b)the gain or loss versus the detuning.

图3 探测场的反射率、增益-吸收与失谐∆p/Γ的关系 (a)θ=π/4时反射率与失谐的关系;(b)θ=π/4时增益-吸收与失谐的关系;(c)Λ=0.06Γ时反射率与失谐的关系;(d)Λ=0.06Γ时增益-吸收与失谐的关系:其他参数同图2Fig.3 .The ref l ectivity and the gain-loss of probe f i eld versus the detuning∆p/Γ:(a)The ref l ectivity versus the detuning when θ = π/4;(b)the gain-loss versus the detuning when θ = π/4;(c)the ref l ectivity versus the detuning when Λ =0.06Γ ;(d)the gain-loss versus the detuning when Λ =0.06Γ .Other parameters are the same as in Fig.2.
接下来,我们来探究出现在PBG2左侧的PBG1.如图4所示,考虑SGC效应(η=1)时的带隙反射率要高于不考虑SGC效应(η=0)的情况.通过调节参数,我们可以实现PBG1反射率大于1的情况(图4(a)红色曲线),此时同样伴随着探测场吸收谱线出现增益(图4(b)插图红色曲线).并且该带隙的谱线线宽远小于自然谱线线宽,在实际应用中可以起到探针的作用.为了探究如何操控PBG1的反射率,我们在图5(a)和图5(b)中展示了PBG1的反射率以及探测场增益-吸收与非相干抽运Λ之间的关系.我们看到,随着Λ由9× 10−4Γ 减小到5× 10−4Γ,PBG1的反射率由1.90降到0.90,且探测场的极化率也不断降低.我们在图5(c)和图5(d)中展示了PBG1反射率和探测场增益-吸收与θ之间的关系.随着cosθ由cos增加到cos,PBG1的反射率由0.77提高到1.35,探测场的极化率也不断增加.这说明对于PBG1,SGC效应的加强(Λ和cosθ增加),同样会使反射率不断提高.也进一步证明,探测场极化率的增加是使系统反射率提高的主要原因.值得注意的是,图5(a)和图5(b)中反射率出现大于1的情况,图5(b)和图5(d)中探测场均会相应地出现增益,但图5(b)和图5(d)中所有探测场增益-吸收曲线均出现增益,图5(a)和图5(b)中仅有部分反射率大于1,这说明探测场出现增益是反射率大于1的必要不充分条件.

图4 η=0(红色实线)和η=1(黑色虚线)情况下探测场的反射率和探测场增益-吸收与失谐∆p/Γ的关系 (a)反射率与失谐的关系;(b)增益-吸收与失谐的关系:其中,Λ=8×10−4Γ,Φ=0.6π,其他参数同图2Fig.4 .The ref l ectivity and the gain-loss of probe f i eld versus the detuning∆p/Γ:(a)The ref l ectivity versus the detuning;(b)the gain-loss versus the detuning.Λ =8×10−4Γ,Φ =0.6π and other parameters are the same as in Fig.2.
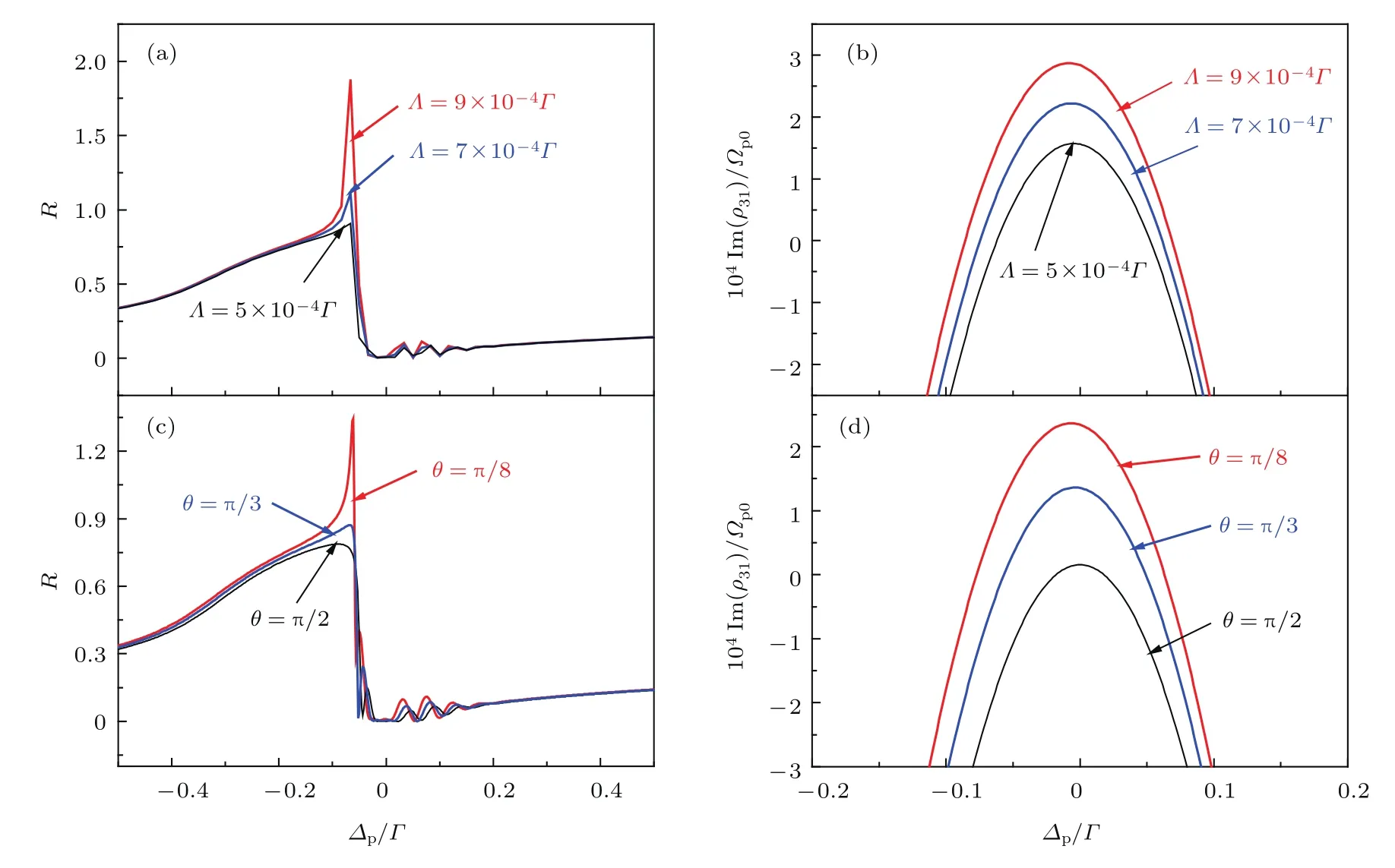
图5 探测场的反射率和探测场增益-吸收与失谐∆p/Γ的关系 (a)反射率与失谐的关系;(b)增益-吸收与失谐的关系;(c)反射率与失谐的关系;(d)增益-吸收与失谐的关系;其他参数同图4Fig.5 .The ref l ectivity and the gain–loss of probe f i eld versus the detuning ∆p/Γ:(a)The ref l ectivity versus the detuning;(b)the gain-loss versus the detuning;(c)the ref l ectivity versus the detuning;(d)the gain-loss versus the detuning.Other parameters are the same as in Fig.4.
综上,不考虑SGC效应时,系统产生的光子带隙较低,SGC效应的引入使反射率大大提高.这是由于SGC效应导致了系统探测场出现增益现象.并且随着SGC效应的增加,探测场的极化率不断增加甚至出现增益现象,PBG的反射率也不断增加,甚至超过1.
4 结 论
本文在一维冷原子光晶格产生可调双光子带隙的基础上考虑了SGC效应,通过合理设置参数分别获得了反射率大于1的两光子带隙.对于之前提高带隙反射率的工作,该工作取得了重要成果,特别是PBG2的反射率可达到1.08,PBG1的反射率可以达到1.9甚至更高.我们通过探究探测场的增益-吸收情况分析反射率提高的原因,发现反射率提高的频率区域探测场的吸收-增益曲线均有提高,甚至在反射率大于1的区域,探测场均出现增益情况.这说明该系统反射率的提高是由于探测场增益导致的.该结论可以用来提高各类光学器件,例如光路由、光二极管和光三极管等的效率[25,29],并且PBG2的线宽小于自然线宽可以用作探针.
