停车场电动汽车充电优化策略*

李淑艳 吴文亮 巫威眺 焦志强

(1.广东交通职业技术学院运输与经济管理学院 广州510650；2.华南理工大学土木与交通学院 广州 510540)

0 引 言

在过去的几十年间，环境恶化、石油资源消耗严重、国际油价波动，各国政府都尽力在减少对进口石油等化石能源的依赖，这些因素极大地促进了交通运输业的电汽化发展。Rahmani等[1]指出，在世界范围内交通行业产生了超过1/4的能源消费和超过1/3的温室气体排放。与传统汽车相比，电动汽车具有环保节能、噪声小、稳定性高等优点。因此，电动汽车作为传统燃油汽车的一个清洁环保的替代品，近年来获得了较大的发展，各国政府推出了一系列的财政补贴和优惠政策，支持电动汽车行业的发展[2]，并鼓励人们购买电动汽车，例如：电动汽车不用摇号、购买电动汽车时给予财政补贴、电动汽车在市中心拥有专用停车位、免费停车、允许电动汽车在高峰时段在公交车专用道或HOV车道上行驶等。电动汽车的数量和市场占有率近年来一直在飞速增长[3]。在不久的将来，电动汽车必将成为人们日常出行的一个重要交通工具。

然而，由于电动汽车的充电时间往往需要数小时[4-5]，充电时间和续航里程把它限制在了相对较短距离的出行上，严重的制约着着电动汽车的实用性。研究表明，对于驾驶员来说，电动汽车的上述缺点带来的不便和负面影响，甚至超过了政府刺激政策带来的影响[6-7]。一般情况下，车辆的平均行驶时间只占到一天总时间的4%～7%[8-9]，大部分时间是处于停泊状态的。因此，未来可建设电动汽车停车场，或在现有普通停车场内加装充电桩，作为电动汽车充电点，在工作日上下班时间段内充分利用工作时间进行间歇式充电[10]，缓解电动汽车的充电问题，提高电动汽车的实用性，显得特别有意义。

关于电动汽车的充电问题，有不少前沿的研究和探讨，大致可分为两大类，其中一类是对于市场化背景下充电问题的研究，如：S. I. Vagropoulos等[11]基于两阶段随机规划理论，提出了在未来市场化背景下，电动汽车聚集充电问题的1个通用模型；Kristoffersen等[12]对电动汽车整个充电过程进行了刻画和描绘。另一类研究主要集中在电动汽车充电对于充电和配电系统的影响方面，S. Habib等[13]研究了不同充电策略下，对双向传输电网的影响(电动汽车可向电网输电，获取利润)；T. Sousa[14]等研究了电动汽车对电网(V2G)有反向输电约束情况下的充电策略，K. Qian等[15]研究了电动汽车充电对变压器老化速度的影响。以上研究为我们提供了很好的借鉴，但其前提和假设条件，均与我国实际有诸多不同，如电价波动、电动汽车可向电网输电的双向传输电网等。在电动汽车保有量迅速增长的当下，结合我国实际情况，需对电动汽车的充电问题进行研究分析。

通过对现阶段停车场大量车辆到达时间、停放时间、通勤出行距离等信息的统计分析，利用非参数估计方法，对未来电动汽车在停车场的停放特征及到达停车场过程中的电量消耗进行预测分析。从停车场运营者的角度出发，给出不同目标下满足车辆充电需求的2种充电策略。

1 模型建立

1.1 问题描述

市中心某停车场，工作日期间的服务对象主要为附近上下班车辆。根据电动汽车的现有规模和增长趋势，未来将会有很大比例的电动汽车在此停靠，为满足停车者的需要并保证停车场的使用率，停车场未来必须设置一定数量带充电桩的停车位，供电动汽车停放和充电使用。假定诸如工作日期间到达停车场的时间分布、停车时长分布等电动汽车的停车特性如与现在的传统燃油汽车群体相同。

笔者拟在停车场未来停车的电动汽车的停车特性基本不变的情况下，以停车场管理者的角度，根据不同的经营目标：停车场电力负荷峰值最小、停车场日电费支出最低，制定不同的充电策略，并对其效果进行对比和分析。

1.2 基本假设及参数定义

提出以下几个基本假设。

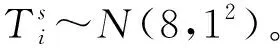
2) 未来电动车停车场中，驾驶员的停车习惯不变，即电动汽车的停车特性和目前调研取得的传统燃油汽车的停放特征一致，包括：到达时间、停车时长、通勤距离等。因为即使是电动汽车也是交通工具，只要使用者出行规律不变，则停放特征就与现在相同。

3) 车辆所需充电量等于通勤过程中的电量消耗量，驾驶员若有充电需求，不同策略下，均需在驾驶员离开之时，需给车辆充满电。

4) 电动车辆到达停车场后即与充电桩相连，停车场可控制何时为车辆充电以及充电功率的大小。

辅助参数定义如下。

决策变量。

1.3 车辆到达停车场后充电的技术路线

图1给出了电动车辆到达停车场后充电的技术路线图，本文的研究对象为正常上下班的通勤车辆，对于有特殊要求的充电车辆，以及停车时间较短，车辆到达后必须立即充电的车辆，将在后续研究中进行。

图1 车辆充电的技术路线图Fig.1 Technology roadmap of vehicle charging

对于停车场而言，即是在以下的技术路线下，对N辆到达的电动车辆并联充电，所以只需确定每个时间段内充电的车辆数和充电功率即可对停车场的电力负荷及总电费支出进行计算。

1.4 电动汽车停车特性分析

文中研究的停靠车辆的特性包括车辆到达时间、车辆的停放时间、车辆离开时间、车辆到达停车场时的电量水平、车辆的电池容量、车辆的最大充电功率等。

1.4.1 车辆到达时间

根据前文假设，研究范围内停车场新增电动汽车在工作日期间到达停车场的时间特征与目前传统汽车群体相同。通过对现有停车场中传统燃油车辆到达时间规律的总结分析，推算出电动汽车的到达时间的分布形态。

根据确定的样本点集合去求解随机变量的分布密度函数问题，有参数估计和非参数估计2种方法[17]。参数估计法又可分为参数回归分析和参数判别分析2种。在参数回归分析中,需首先假定数据分布符合线性、指数性等某种特定的性态,然后在目标函数族中寻找特定的解,即标定回归模型中的未知参数。在参数判别分析中,则需要假定作为判别依据的、随机取值的数据样本在各个可能的类别中都服从特定的分布。理论研究和经验表明,参数模型的这种基本假定与实际的物理模型之间常常存在较大的差异,因而有时求解的结果偏差较大，不能作为描述变量分布的依据[18]。由于上述缺陷，Rosenblatt[19]提出了非参数估计方法，即核密度估计方法。该方法事先不对数据分布附加任何假定，不利用有关数据分布的先验知识，是一种从数据样本本身出发研究数据分布特征的方法，能够有效的避免事先假定带来的误差。

笔者利用核密度估计对车辆到达的时间分布特性进行描述。核密度估计函数的表达式为

(1)

(2)

(3)

工作日期间，对广州市中心区62个停车场的停车状况进行实地调研，统计所有车辆的到达停车场的时间信息，结果如图2所示。由于目前还未建立专门的可供电动汽车充电的停车场，此处调查的是所有乘用小汽车(包括电动和传统燃油汽车)的到达信息。

依据以上车辆到达时刻的样本信息，对工作日期间车辆到达停车场的时刻累积分布特性进行核密度函数拟合，其中σs=4.14h，R/1.34=5.58h，n=13 470，h=0.655；核密度的具体表达式为

(4)

绘制拟合曲线，结果见图3，用核密度函数对车辆到达时刻的概率分布进行估计，存在一定误差，但基本趋势吻合，误差在可接受范围内，拟合效果良好。

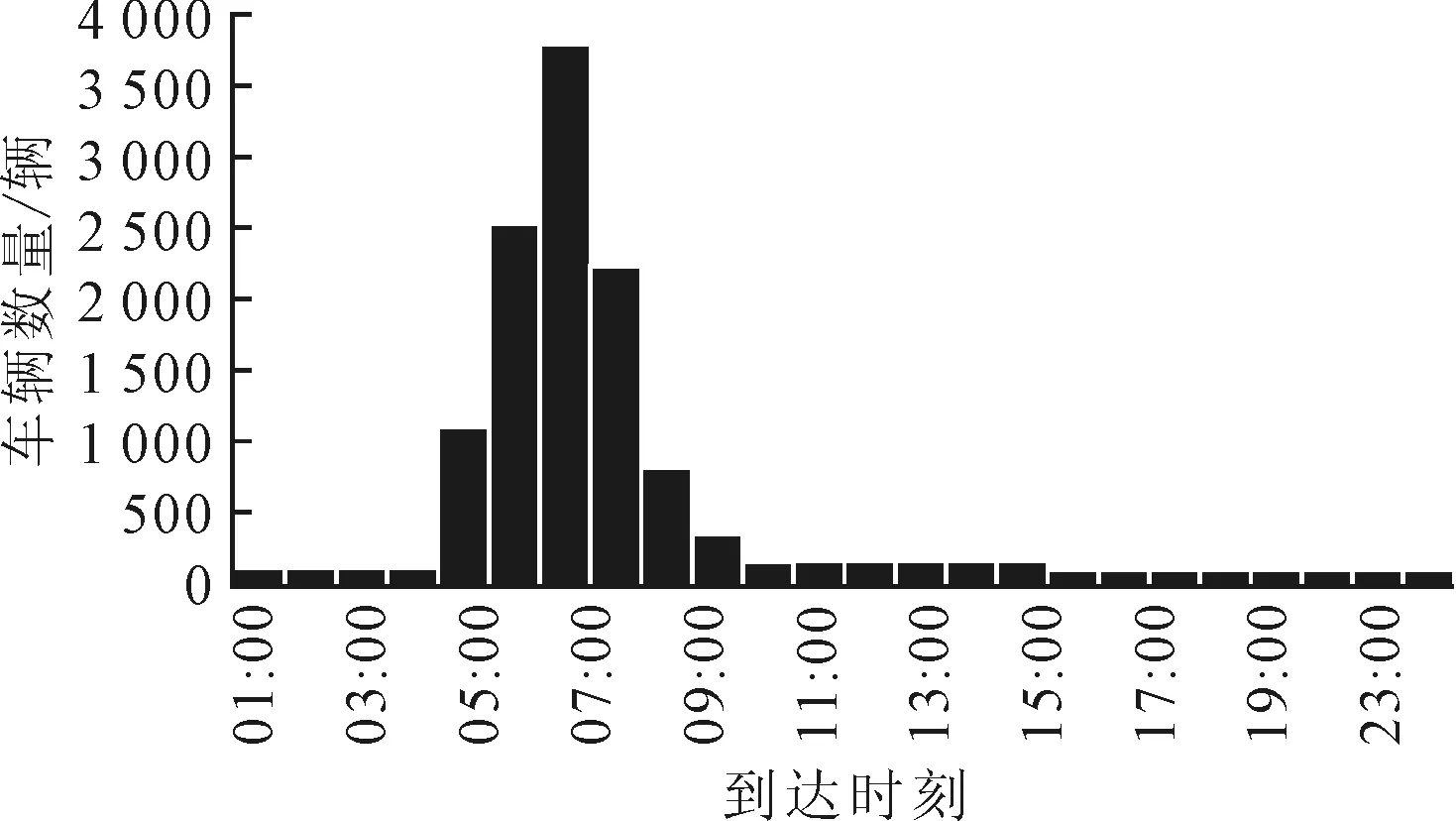
图2 现阶段车辆到达时间的柱状图Fig.2 Histogram of arrival time of vehicles for now

图3 到达时间累积分布概率及核密度函数拟合Fig.3 Cumulative distribution of arrival time and kernel density function fitting

1.4.2 电动汽车到达停车场过程中的耗电量

依据前文假设，工作日期间通勤车辆自居住地出发时，车辆电量饱满，车辆在停放时间内所需的充电量等于到达停车场过程中的电量消耗量。未来，可以凭借驾驶员与停车场之间的更多信息交互(停车预约等)，精准地获得车辆到达停车场时的电量水平，现阶段则通过车辆的出行距离特征和综合工况下电动汽车单位行驶距离的电量消耗，对到达车辆的电量消耗信息进行尽可能准确的估计。

表1给出了几款目前我国主流的电动汽车的技术参数，根据表中信息，结合相关研究[20]，确定综合工况下电动汽车单位行驶距离的耗电量为0.178 kW/km。

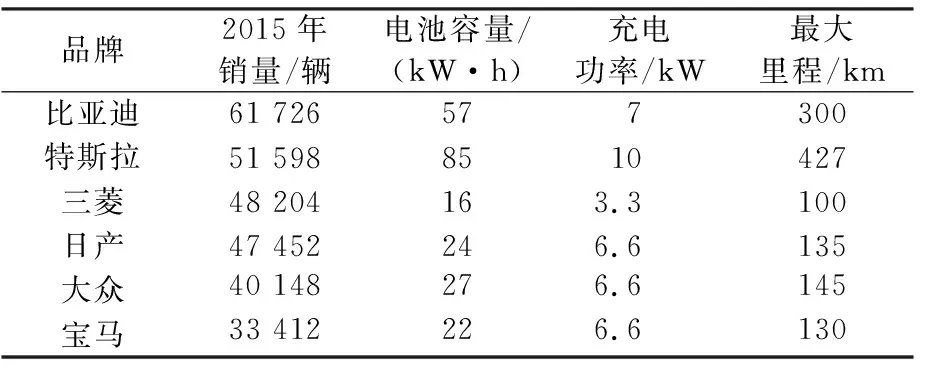
表1 国内主流电动车辆的技术特性Tab.1 Technical characteristics of domesticmainstream EVs

依据本文上节中对停车场驾驶员的问卷调研，提取出调研信息内驾驶员工作日期间到达停车场时的行驶距离数据，如图4所示。

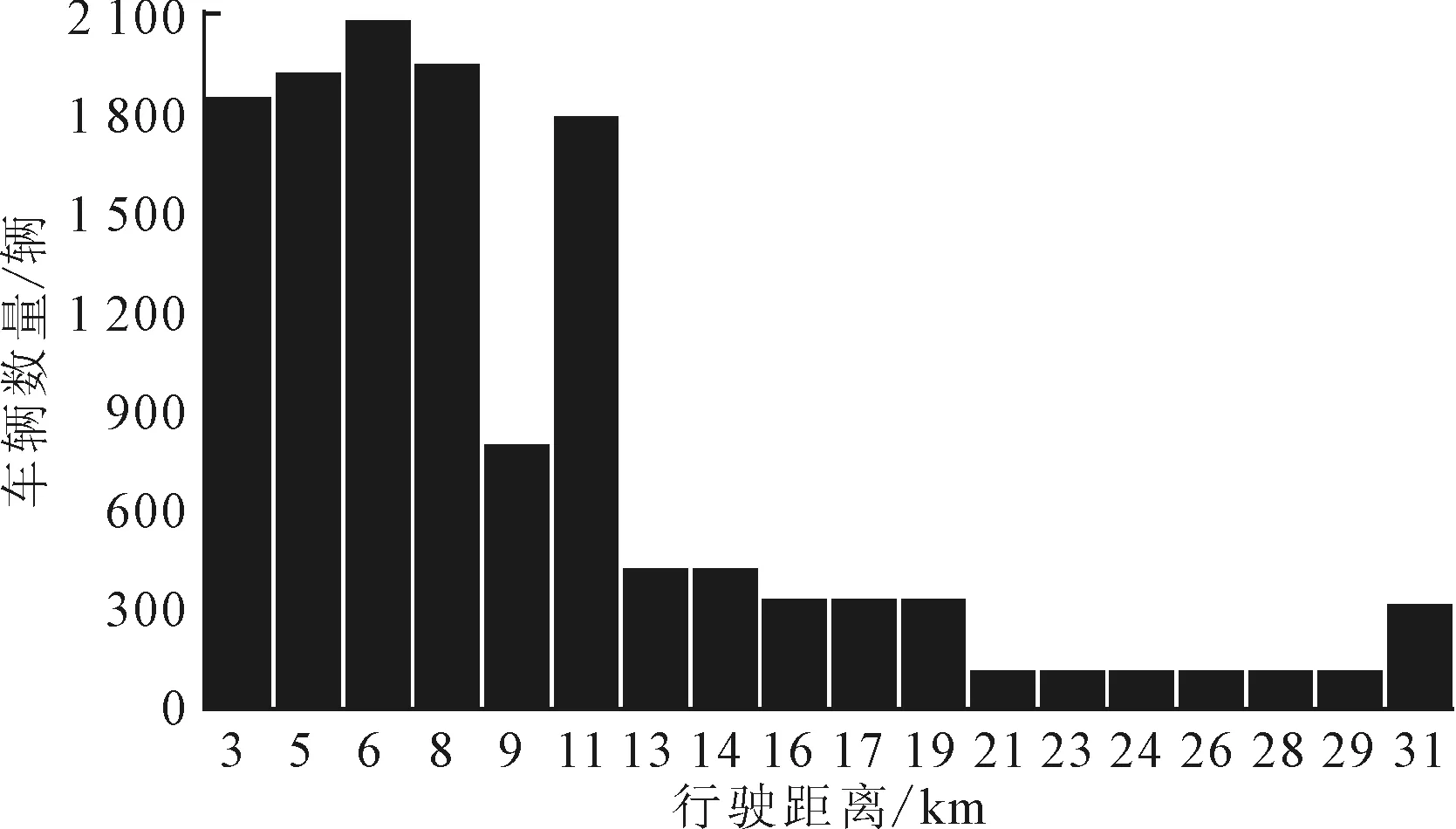
图4 驾驶员到达停车场时的行驶距离Fig.4 Travel distance of parking vehicles

根据驾驶员工作日通勤出行情况下到达停车场时的行驶距离数据，结合综合工况下电动汽车单位行驶距离的耗电量，推算出电动车辆到达停车场过程中的电量消耗信息，如图5所示。

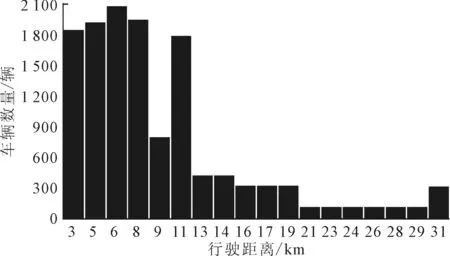
图5 电动车辆到达停车场过程中的电量消耗Fig.5 Power used by EVs to arrive the parking lot

依据以上车辆到达停车场过程中的电量消耗信息，对工作日期间车辆到达停车场过程中的电量消耗累积分布概率进行核密度函数拟合，其中σs=2.294 kW·h，R/1.34=0.687 kW·h，n=13 470，h=0.109；核密度的具体表达式为

(5)

绘制拟合曲线，结果如图6所示，用核密度函数对车辆到达过程中的耗电量概率分布进行估计，存在一定误差，但基本趋势吻合，误差在可接受范围内，拟合效果良好。

图6 耗电量累积分布概率及核密度函数拟合Fig.6 Cumulative distribution of used power and kernel density function fitting

1.4.3 停车场车辆数量

依据上文对大量停放车辆的调研信息，得出工作日期间1 d各时间段内停车场停放的车辆数量，如图7所示。假设未来停车场停放的车辆数量规律与此相同。

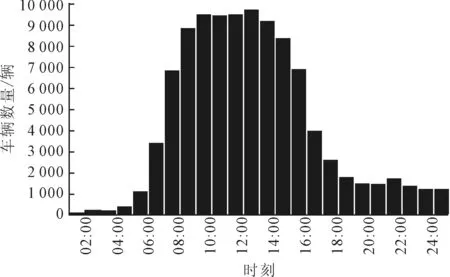
图7 停车场内的车辆数量Fig.7 Number of electricity vehicles in the parking lot

本文研究区域内，任意时间段内，车辆到达停车场时的行驶里程呈均匀分布状态。依据1.4.1车辆到达时间的概率分布和1.4.2节车辆到达过程中的耗电量概率分布及1.4.3节1 d内各个时段内停车场的停车数量，即可推算出停车场特定时间段内到达的车辆数及车辆到达过程中的耗电量。

1.5 充电策略

1.5.1 策略1：随到随充

对于每1个到达停车场的电动汽车，从其到达停车场的时刻开始，即以车辆最大功率对其进行充电，直至充满为止，见图8。

图8 随到随充技术路线Fig.8 The flow chart of instant charging strategy

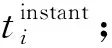
1.5.2 策略2：停车场电力负荷峰值最小

随到随充的充电策略可能会导致在某个时间段，停车场电力负荷过大，特别是当大量的车辆在特定时间段内集中、连续到达时，停车场电力系统需要满足最大负荷时的需要。这种情况下，对停车场的安全性影响较大，且需要较高水平的供电线路以避免电压衰减。一般而言，作为停车场的管理者，是不希望停车场的电力负荷很大的，因为需要增加成本并带来安全隐患。基于上述原因，本文提出使得停车场电力负荷峰值最小的充电策略。

目标函数为

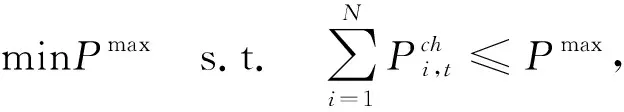
(6)

(7)

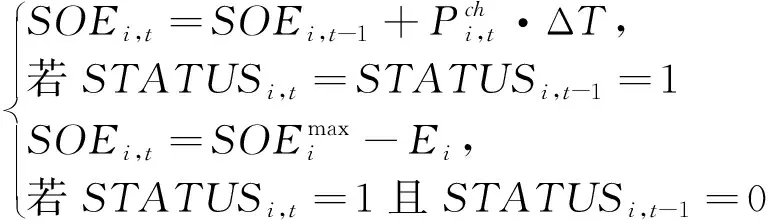
(8)

(9)

式中：Pmax为停车场为车辆充电时的最大负荷功率，目标函数使得停车场的电力负荷峰值最小；若车辆i在t时刻停靠在停车场，则STATUSi,t=1，否则STATUSi,t=0，式(5)表示车辆停靠在停车场时的充电功率不超过车辆设计的最大充电功率；SOEi,t表示车辆i在t时刻的电量水平，式(6)描述了车辆i的电量变化状态；式(7)表示停车场为车辆充满电。

1.5.3 策略3：总电费最小

目标函数为

(10)

(11)

(12)

目标函数表示对于每一辆充电车辆i，充电所需的花费最小，其他约束条件各式的意义与策略2中的相同。

1.6 模型求解

策略1中停车场各时段的负荷为单个车辆充电功率的累加，图1的流程图中给出了单个车辆在各个时段的充电功率的计算过程，累加后结合各个时段的电费水平即可求得电费的总支出。

策略2与策略3均为传统线性规划问题，现以策略3为例进行模型求解说明，通过构造拉格朗日函数，利用KKT条件进行求解。

拉格朗日函数如下，其中a，b，c为拉格朗日乘子。

函数的KKT条件如下：

λt-a-b+c=0

(13)

(14)

(15)

(16)

2 算例分析

考虑未来市中心1个拥有250个充电桩，可供电动汽车停车及充电的停车场，根据本文1.4.3部分对该地区车辆到达时间及停放规律的分析，确定1 d各时段内停放的电动汽车数量，见图9。

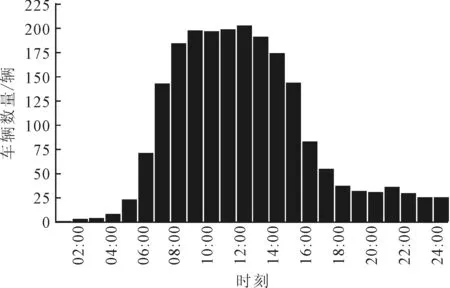
图9 停车场停放车辆数Fig.9 Number of electricity vehicles in the parking lot

城市商业用电峰谷分时电价标准见图10。

根据前文对该地区车辆到达时间、停放规律、电动车辆耗电量的分析，分别按照策略1、策略2、策略3对车辆进行充电，并对不同策略下停车场的电力负荷和总电费支出进行对比分析。

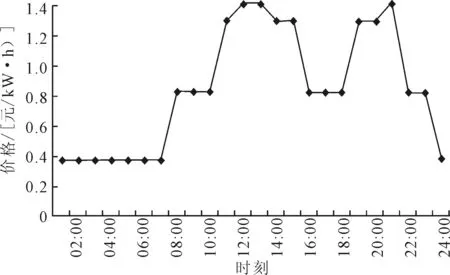
图10 电价波动图Fig.10 Electricity price fluctuation figure

图11给出了按照策略1和策略2充电时停车场的电力负荷状况，根据其在各个时段的负载情况和分时电价信息，可以得到策略1和策略2运营状态下，停车场的电费消耗。不对充电过程做任何优化控制，施行随到随充策略时，停车场的电力负荷在08：00左右达到峰值526 kW，因为大部分的车辆在这个时间点到达停车场。整体上看07：00—09：00的电力负载明显高于其他时间段，主要是因为，根据概率分布函数，停车的车辆中有将近50%的车辆在这个时间段到达停车场。如果把电力负荷平均到1 d的各个时段，可以得到各个时段的电力负荷在92 kW左右。为了避免短时间内负荷过高带来的电压下降和对电力系统的过高要求，笔者提出了策略2，使得停车场的电力负荷峰值最小化。从下图的结果中我们可以看出，在满足所有需求的情况下，策略2可以使电力峰值的负荷下降到158 kW左右，这是具有很大的实际应用意义的。

图11 策略1、2下停车场电力负荷Fig.11 Power load of parking lot under strategy 1 and 2

策略3给出了使得停车场在满足车辆充电需求的情况下，总电费最小的充电方法，该策略下，停车场各时段充电力负荷很大程度上取决于不同时段的电价水平。

在策略3中(见图12)，07：00—09：00之间，停车场的电力负荷达到峰值，主要是因为这个时间段内，有大量的车辆到达，且电价相对较低。在电价相对较高的11：00—15：00和19：00—21：00，停车场的充电功率相对较低，甚至为零。尽管13：00之前，大部分的车辆都已经到达了停车场，但是因为11：00—13：00电价最高，所以这个时间段内，停车场的充电负荷不大。在15：00—18：00之间，出现了负载高峰，最高负载达到了618 kW，是因为这段时间内电价相对较低，且11：00—15：00电价较高，对到达的大部分车辆没有充电，为了实现电费最少的目标，导致停车场的最大电力负荷远超过了策略1和策略2中最大高峰负荷。但是这3种策略下，由电网输送给停车场的总电量都是2 208 kWh。

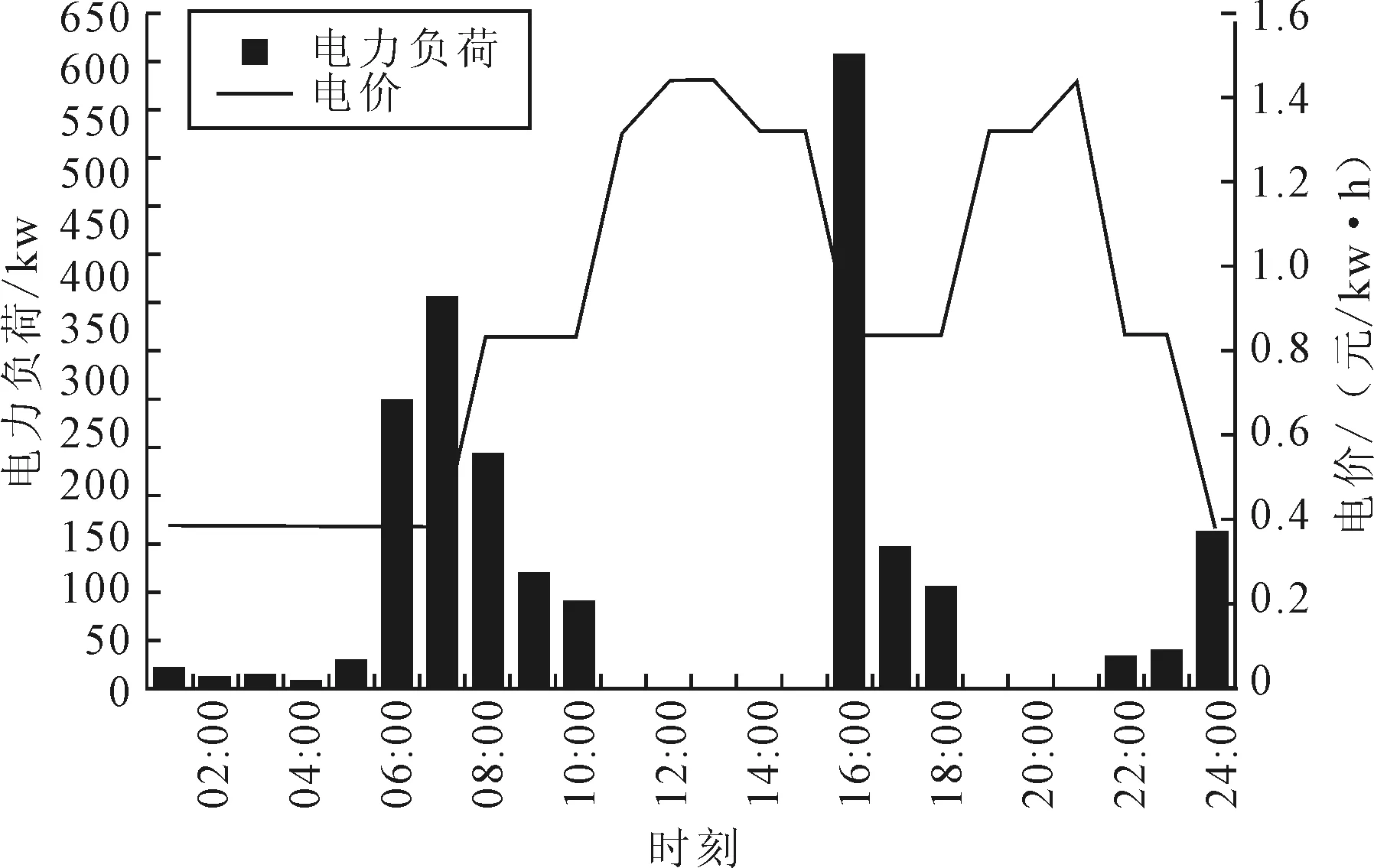
图12 策略3下停车场电力负荷Fig.12 Power load of parking lot under strategy 3

不同策略下电动汽车停车场的电力负荷峰值和总电费支出对比分析，见表2。

表2 3种充电策略下停车场的运营数据Tab.2 Operational data under different strategies

在以上的3种策略中都假定所有的电动汽车连接上停车场的充电桩后，采用相同的充电策略，但是，在实际情况中，不同的停车者，可能有自己的特殊偏好，例如，要求停车场立即给自己的车辆充电等。停车者没有特殊的要求时，从停车场运营者的角度出发，按照策略2或策略3充电。

3 结束语

本文通过计算，给出了未来不同运营策略下电动停车场为车辆供电时的电力负荷和电费支出。首先运用核密度函数进行估计，对车辆到达停车场的时间、电量的消耗量的概率分布进行了较为精确的估计。

其次，结合不同时间段的电价信息，给出了3种控制策略下，停车场1 d内各个时间段的电力负荷和所需要支付的总电费。

基于非参数检验的核密度估计，可根据从历史数据本身，相对准确的描述出数据的分布特征。通过市场电价结合不同的目标函数及约束函数，推导出了不同时间段对应的电力负荷和不同策略下的总电费。

未来停车场和驾驶员停车信息完全对称时，停车场可通过停车预约信息，可以比本文基于历史样本的估计方法更加准确地把握到停车者的停车时长和所需电量，然后可以根据本文的计算模型，得出更加精确地供电策略。本文从运营者角度提出了2种策略，然而，在没有激励的情况下，用户可能偏好随到随充策略以减少风险，下一步将研究通过充电价格机制建立用户选择模型，从而实现用户与运营者的双赢。

研究发现，充电的效率和便捷性是影响充电用户选择停车场的重要因素。停车场充电策略的变化必会对充电效率产生影响，进而影响用户对停车场的选择和停车场的效益，本次研究未对不同充电策略下用户的选择问题做具体刻画，接下来，团队将更加全面地对电动汽车充电涉及到的各个方面问题，进行综合分析，更加贴合实际，力争为未来电动汽车占据更大市场份额时，优化完善其充电策略，提供一定的参考和借鉴作用。