圆中角的应用

文 /王宗俊

在圆中，圆心角与圆周角是最常见的角.它们与弦、弧和扇形面积的联系比较密切，是中考命题的重点.下面举例说明圆中角的各种应用.

一、求角的大小

1.利用圆心角求圆周角

例 1如图1，在⊙O中，OA⊥BC，∠AOC=50°，则∠ADB的度数为（ ）.

A．15° B．25° C．30° D．50°

解析：如图1，连接OB.

∵OA⊥BC，

图1

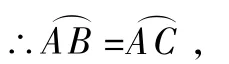
又∵∠AOC=50°，

∴∠AOB=∠AOC=50°，

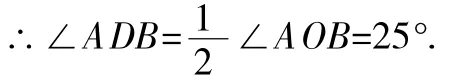
选B．

2.利用圆周角求圆心角

例 2如图2，在⊙O中，OC⊥AB，∠ADC=32°，则∠OBA的度数是（ ）.

A．64° B．58° C．32° D．26°

∴∠2=∠3．

∵∠2=2∠1=2×32°=64°，

∴∠3=64°.

在Rt△OBE中，∠OEB=90°，

∴∠B=90°-∠3=90°-64°=26°.

选D．

图2

3.利用直径所对的圆周角是直角求角

例3如图3，AB为⊙O的直径，CD是⊙O的弦，∠ADC=35°，则∠CAB的度数为（ ）.

A．35° B．45° C．55° D．65°

解析：由圆周角定理得∠ABC=∠ADC=35°，

∵AB为⊙O的直径，

∴∠ACB=90°，

∴∠CAB=90°-∠ABC=55°.

选C．

图3

4.利用圆内接四边形的对角互补求角

例 4如图4，点B，C，D在⊙O上，若∠BCD=130°，则∠BOD的度数是（ ）.

A．50° B．60° C．80° D．100°

解析：如图4，在圆上取一点A，连接AB，AD，

∵ 点A，B，C，D在⊙O上，∠BCD=130°，

∴∠BAD=50°，

∴∠BOD=100°.

选D．

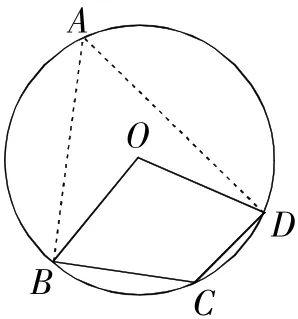
图4

5.利用圆心角、圆周角求其他角

例5如图5，AB是⊙O的直径，MN是⊙O的切线，切点为N，如果∠MNB=52°，则∠NOA的度数为（ ）.

A．76° B．56° C．54° D．52°

解析：∵MN是⊙O的切线，

∴ON⊥NM，

∴∠ONM=90°，

∴∠ONB=90°-∠MNB=90°-52°=38°，

∵ON=OB，

∴∠B=∠ONB=38°，

∴∠NOA=2∠B=76°．

选A．

图5

二、求弦长

例 6如图6，点A，B，C，D都在半径为2的⊙O上，若OA⊥BC，∠CDA=30°，则弦BC的长为（ ）.

解析：∵OA⊥BC，

∴∠AOB=2∠CDA=60°，

选D．

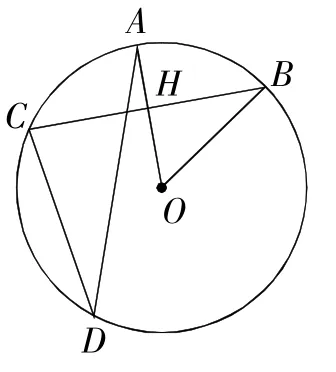
图6

三、求弧长

例7如图7，AB是⊙O的直径，点D为⊙O上一点，且∠ABD=30°，BO=4，则的长为（）.

解析：连接OD.

∵∠ABD=30°，

∴∠AOD=2∠ABD=60°，

∴∠BOD=120°，

选D．

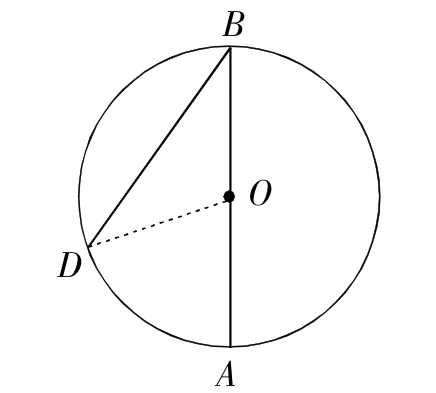
图7

四、求面积

例 8如图8，AB是⊙O的直径，CD是弦，∠BCD=30°，OA=2，则阴影部分的面积是（ ）.

解析：∵∠BCD=30°，

∴∠BOD=60°，

∵AB是⊙O的直径，CD是弦，OA=2，

选B．

图8