基于地质大数据的泥石流灾害易发性评价
2018-12-14张永宏葛涛涛夏广浩
张永宏,葛涛涛,田 伟,夏广浩,何 静
(1.南京信息工程大学 信息与控制学院,南京210044; 2.南京信息工程大学 计算机与软件学院,南京 210044)(*通信作者电子邮箱tw@nuist.edu.cn)
0 引言
随着大数据时代的到来,大数据所创造的价值渗透在当今生活的方方面面,已成为高校和企业的重点研究对象。传统方法难以处理量大、异构、更新快速的数据[1],而神经网络特征提取能力强,易于整合多源信息,对动态变化的数据适应性高的特点,足够使其成为大数据价值转化的纽带;同时,大数据也为神经网络训练供应了足够多的训练样本。伴随着计算机软硬件技术的发展,神经网络应用到了各个领域,如语音大数据分析[2]、医学大数据分析[3]、农业大数据分析[4]以及电力大数据分析[5]等,大数据结合神经网络已成为当下推动社会与科学发展的重要动力。
长期地质调查工作积累了大量的地质原始数据,通过遥感、钻探、物探等手段获得多源、多模态、多时态的地质数据具有大数据的典型特性,即地质大数据。泥石流是发生在山区的一种突发性地质灾害,其易发性评价以地质环境为基础,根据地质灾害现状,静态考察泥石流灾害在一定区域内发生的可能性大小,它的强弱同时受多种外在因素和内在因素的共同影响[6]。泥石流易发性评价的实施可以为当地公共设施建立、居民人生安全以及防灾减灾提供巨大帮助。
目前比较常用的泥石流易发性的评价方法有层次分析法[7]、模糊数学[8-9]、逻辑回归[6]等,也有学者将已有方法结合使用,取长补短[10]。这些算法在取得不错成绩的同时也存在一些不足之处,如:层次分析法指标体系的提出需要有专家系统的支持,且泥石流指标维度较多,标度工作量太大;模糊综合评价计算复杂,确定泥石流指标权重向量时过于主观,造成泥石流易发性评价精度不高;逻辑回归属于广义线性回归模型,泥石流易发性评价指标中的多重共线性问题对其影响较大。
从上述传统泥石流易发性评价方法来看,它们存在一些共同的局限性:评价主观,难以处理多维度的大数据信息。神经网络具有良好的非线性映射能力,能够在海量地质数据中揭示数据内部联系,对未来作出精准的预测,在泥石流易发性评价应用中成果显著[11]; 然而神经网络存在学习速度慢,难以处理非平衡数据等问题,使其作用得不到充分发挥,并且面对地质大数据,无法找出输入指标对易发性的影响程度。针对传统方法的不足,本文基于神经网络,结合Borderline-SMOTE(Synthetic Minority Oversampling TEchnique)算法,遗传算法(Genetic Algorithm, GA)和平均影响值(Mean Impact Value, MIV)算法对影响泥石流发生的地质大数据进行分析与挖掘,并建立泥石流易发性评价模型。实验证明,在研究地处“一带一路”重要节点之一的雅鲁藏布江中上游流域泥石流孕灾环境的基础上,使用TensorFlow框架搭建的神经网络结合优化算法可以对研究区域内山地泥石流灾害易发性进行准确的评价。
1 泥石流易发性评价模型框架
为了应对区域泥石流易发性评价所面临的挑战,本文构建了一种能够客观准确地评价区域泥石流易发性的模型框架,如图1所示。本框架一共包含5层,自下而上分别为数据层、学习框架层、易发性评价方法层、易发性评价技术层以及应用层。该泥石流易发性评价框架中,各个层次核心功能描述如下:
数据层 数据层主要提供遥感图像,地形图,地质图,灾害历史事件等基础资料。对地质大数据数据库的管理包括定义、检索、修改、增减等操作,并建立数据字典。由于泥石流沟的基础数据以及各种孕灾环境因子处于动态变化之中,所以该层应具有开放性,有利于随时更新和维护数据库中的存储数据。
学习框架层 TensorFlow学习框架能够在多种运行环境下使用,并且在前端支持多种主流语言调用其API(Application Programming Interface)。该框架封装了当下流行的众多神经网络模型,可以根据需要构建和实现所需要的网络模型。本文在Windows系统下调用TensorFlow框架,通过import命令导入待使用的数据库,并使用Python编程语言搭建能够准确评价泥石流易发程度的学习架构。
易发性评价方法层 泥石流成灾条件复杂,影响其易发程度的因素随机且模糊。BP(Back Propagation)神经网络无须建立确定的模型,只需根据一定量的样本来学习研究对象的内部结构,便可完成输入集合与输出结果之间的非线性映射。网络采取随机初始化的方式获取权值和阈值,导致分类效率低下,易陷入局部最优, 因此,采用遗传算法搜索全局最优权值和阈值,可缩减训练时间,提升网络的泛化性能。
易发性评价技术层 在易发性评价过程中,分类器能够对类别分布均衡的数据作较为精准的分类; 然而,实际生活中,不同易发等级的数据极不平衡, 且虽然网络能够逼近任意非线性关系,但是难以表达输入指标与模型的相关性, 因此,需要设计易发性评价方法优化技术,在解决类别间数据不平衡问题对分类器影响的同时筛选输入指标。分别采用重采样技术和平均影响值算法,达成上述优化目标。
应用层 泥石流易发性评价实际应用中,将已知的历史灾害数据集按训练集、验证集、测试集进行合理的分配。设网络的训练样本数据集为{(x1,d1), (x2,d2),…,(xm,dm)},xi为泥石流i的特征向量,di为对应的泥石流易发性等级标签,di∈{1,2,…,r},r为标签的类别数,m为训练的样本个数。基于泥石流易发性评价方法层和技术层,实现类别不平衡数据下,根据输入孕灾环境,快速准确地评价区域泥石流易发性,并获取影响当地泥石流发生的主要影响因子。
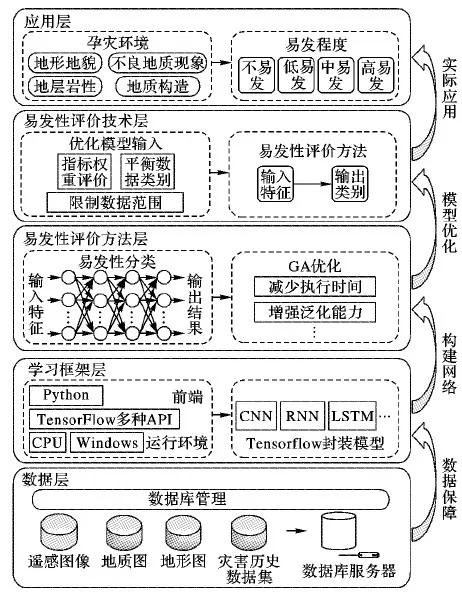
图1 泥石流易发性评价模型框架
2 泥石流易发性评价方法
本文对于泥石流易发性的评价包含两个基本过程:基于神经网络的泥石流易发性模型搭建及其技术优化,所以将泥石流易发性评价问题划分为以下3个步骤:
1)从采集到的泥石流灾害系统的众多影响因子中提取能够准确反映区域特征的泥石流易发性评估指标,对其作归一化和过采样Borderline-SMOTE的处理;
2)构建评价泥石流易发性神经网络模型,将过采样后的训练数据输入到网络进行训练,调整并确定模型参数,并对已经确定结构的神经网络采用遗传算法进行优化,找到全局最优权值和阈值,提升模型的效率和泛化性能;
3)使用MIV算法探讨指标因子与上述GA_BP模型的相关性,删减冗余信息,最后通过网络Softmax分类器计算模型输出结果。
技术路线图如图2所示。
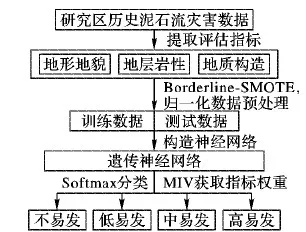
图2 泥石流易发性分类技术路线
最后采用基于受试者工作特征曲线(Receiver Operating Characteristic Curve, ROC)分析的AUC(Area Under the Curve)方法评估模型的准确性和可靠性。
2.1 重采样技术
过采样技术在解决数据不平衡分类问题中具有广泛的应用价值[12-13]。在山地灾害研究中,往往可以发现,中易发性的地区占绝大多数,而其他易发性的地区是相对较少的。分类过程中,少数类数据稀少是影响神经网络分类精度的主要原因之一。本文使用一种基于边界的SMOTE算法(Borderline-SMOTE),其具体的方法为:
首先使用K近邻算法计算少数类样本集T中每一个样本在训练集x中的K近邻样本集P,并分析其中属于多数类样本集T′的比例:若多数类样本占少数则直接将该样本放回少数类样本集;若多数类样本占多数则将该样本作为边界样本,放至边界(Borderline)集合F中。计算边界样本集中每个样本Ti在T中的K近邻,并从中随机选取一个样本Tj,使用Ti与Tj结合SMOTE算法,由式(1)生成新的少数类样本Tnew,合成的新样本Tnew加入到原始样本集形成新的样本集Xinput。
Tnew=Ti+random(0,1)*|Ti-Tj|
(1)
算法描述伪代码如下:
算法1 过采样。
InputK,m,T,T′,x;
OutputXinput。
1)
fori=1 to |T| do
2)
计算少数类样本中Ti在训练集x中的K近邻集合P;
3)
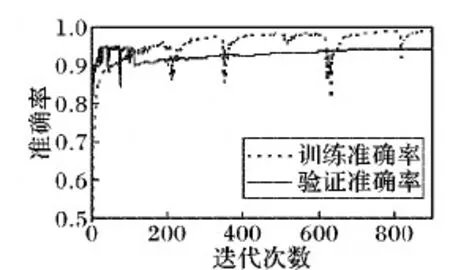
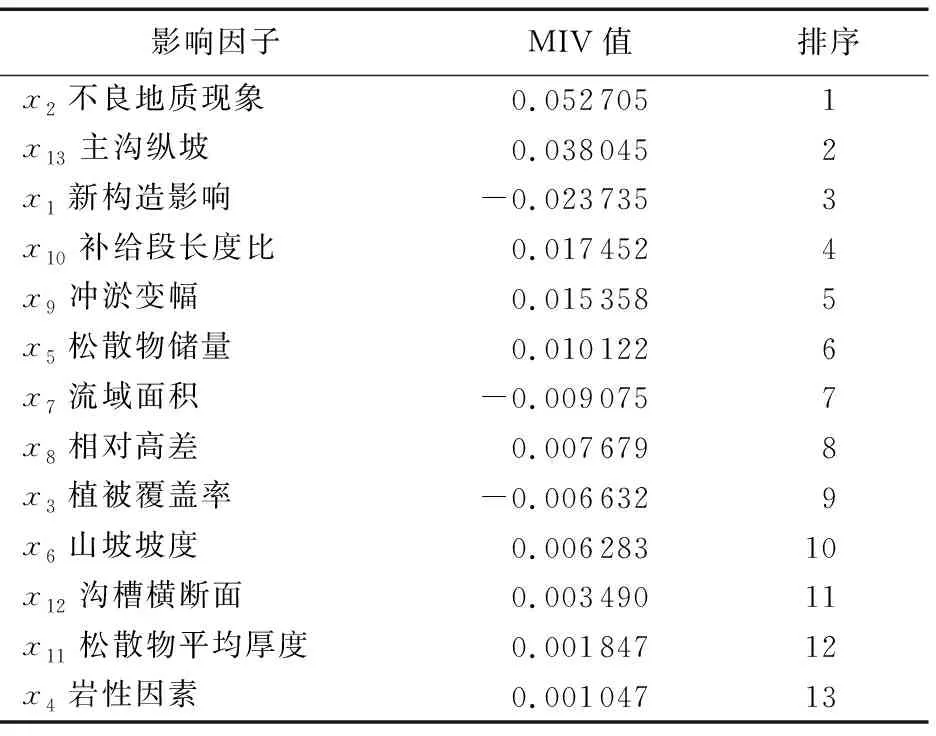
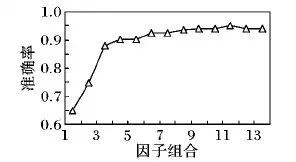
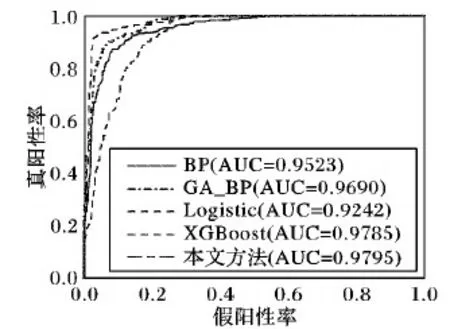
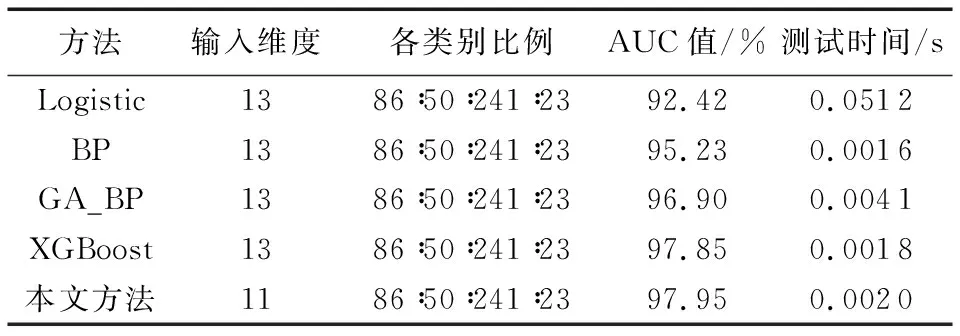
if (K/2<|P∩T′| 4) 将Ti加入到边界集合F中; 5) 计算集合F中元素在少数类样本的K近邻; 6) end if 7) end for 8) z=|T′|-|F|; 9) whilez≠0 do 10) 随机选择集合F中的Ti; 11) diff=Ti与其近邻Tj之间的距离; 12) gap=0到1之间的随机数; 13) Tnew=Ti+gap*diff; 14) Xinput=Tnew∪x 15) z=z-1; 16) end while 17) returnXinput 人工神经网络(Artificial Neural Network, ANN)是一种模仿生物神经系统处理信息的数学模型,BP神经网络作为ANN中最精华的部分,通常具有3层及以上的网络结构,包括输入层、输出层以及隐藏层, 其功能包括信号的前向传播和误差的反向传播。 由于网络各层的激活函数和学习规则等存在差异,所以在神经网络的输入端应对重采样后的数据使用归一化算法,定义如下: xnew=(xij-xi_min)/(xi max-xi_min) (2) 样本x完成归一化后,样本集Xinput离开输入层进入隐藏层,经传递函数(如Tanh、Relu等函数,经实验对比,本文使用Tanh函数)激活后继续往下一层传递,直至输出层,各层输出公式为: (3) 其中:f(·)表示传递函数;θ={w,b}表示网络参数,其中w为权重,b为阈值。网络的输出层采用Softmax分类器进行分类识别,其公式定义为: (4) 式中:p(di=k|xi)表示样本xi识别为第k个类别的概率;hλ(xi)是r行1列的向量,即r个类别分类器输出的也是一个r维向量,所有行元素之和为1;λ1,λ2,…,λr∈Rn+1是分类器的参数,且构成参数矩阵λ。对于xi,选择输出向量中最大概率对应的k值作为分类结果。 模型的训练目标是通过寻找一组最优参数θ*={w*,b*},使预测值与实际值误差最小,即在训练过程中,使代价函数J(λ)达到最小,代价函数J(λ)定义为: (5) 式中:1{·}是一个指示性函数,大括号里的值为真返回1; 否则返回0。经过实验,利用误差逆传播和Adam优化算法可实现式(5)达到最小,结束训练。 由上可知,BP算法的权重和阈值对学习结果存在很大影响,而网络采用随机初始化的方式使其存在波动、难以收敛或训练速度慢的问题,最终导致学习结果不理想。遗传算法是一种基于自然选择和遗传变异等自然界进化过程的计算模型,具有很强的全局搜索能力和全局优化性能[14]。遗传算法将前述神经网络中的初始权值和阈值作为种群中的个体,采用二进制编码为其编码,编码长度由BP神经网络的结构而定,包括网络层数及各层节点数。其中隐层神经元个数通常由式(6)确定: (6) 式中:l为隐层节点数,n为输入层节点数,r为输出层节点数,α为整数,取值范围为1~10。一组个体的集合作为种群(pop),种群规模应根据具体问题选择合适的数量,初始种群规模设为S;最大遗传代数设为Gen。遗传算法优化神经网络权值和阈值主要分为两步: 第一步, 构造适应度函数用于考察个体的优劣情况,本文设定为神经网络代价函数的倒数。输出值与期望值之差越小,适应度值越高,个体越有优势,反之则会在进化过程中被淘汰。 第二步,进行遗传操作:1)根据计算的适应度,进行个体的选择。首先通过最优策略选出适应度最高的最佳个体,直接遗传给下一代种群,其余个体通过概率值进行选择,公式如下: (7) 其中fi为个体i的适应度值。2)选择种群中的一对作为父体,以一定的交叉概率Pc进行交叉配对,产生另外两个新个体。3)随机选择种群中的个体,以特定概率Pm进行变异,即通过改变个体中的某一基因位而产生新个体。4)最后进行循环操作,当遗传代数小于最大遗传次数时,转至第一步,继续运行。直至指定的进化次数时停止运行,从种群中选择适应度最高的个体,输出对应的权值w和阈值b。最后将这组权值和阈值应用于BP神经网络中,当达到目标准确率(Aim_accuracy)时,结束训练,输出分类结果。算法伪代码描述如下: 算法2 遗传神经网络(GA_BP)。 输入Pm,Pc,Gen,Aim_accuracy,S,Xinput; 输出 GA_BP网络结构和参数。 1) 初始化遗传算法的参数和种群pop; 2) t=0; 3) while(t 4) 基于Xinput数据集计算S组w和b的网络误差; 5) 计算个体适应度; 6) 根据适应度,从pop(t) 中选择优质下一代pop(t+1); 6) if (random(0,1) 7) 执行交叉操作; 8) end if 9) if (random(0,1) 10) 执行变异操作; 11) end if 12) end while 13) 选择具有最佳适应度的一组w和b; 14) accuracy=0 15) while(accuracy 16) 使用最优w和b迭代计算输出结果; 17) 计算准确率; 18) 最小化损失函数; 19) 更新w和b; 20) end while 21) return GA_BP网络结构和参数 影响泥石流易发性的因子众多,在构建泥石流易发性模型时,应该考虑特征因子影响力的大小,但是神经网络无法从已有的特征中确定特征所占的权重。MIV值可作为确定输入神经元对输出神经元影响大小的指标[15],所以本文使用该算法确定泥石流易发性分类中各个因素与网络的相关程度,删减冗余信息,提升分类精度和速度,同时可为研究人员野外勘察提供参考。具体过程如下: 将训练样本Xinput中每一个样本在其原有基础上加减10%,形成两个新的训练样本A1、A2。将这两个新的训练样本代入已经训练好的网络中,得到另外两个仿真结果B1、B2。将B1-B2的值作为改变该特征对输出结果产生的影响变化值IV。最后将该影响值按灾害观测数求取平均值。按照上述步骤分别算出n个特征的平均影响值MIV,最后根据平均影响值绝对值的大小对特征进行从大到小排序,并构建包括排序值前1至前13个因子的13种因子组合。利用前述GA_BP算法对比计算13种组合分类效果。算法描述伪代码如下: 算法3 指标评价与选择。 输入 GA_BP网络,Xinput; 输出 最优指标组合x*。 1) fori=0 tondo 2) A1=x,A2=x; 3) A1[:,i] =A[:,i]*1.1; 4) A2[:,i] =A[:,i]*0.9; 5) 分别计算数据集A1和A2在GA_BP的预测结果B1和B2; 6) IV=B1-B2; 7) MIV=总体IV的均值; 8) end for; 9) 按照MIV值从大到小的顺序为指标因子排序; 10) 根据排序构建13组输入组合; 11) 计算各组合在GA_BP 模型的输出准确率; 12) 根据准确率大小选择最优组合x*作为输入; 13) returnx* 本次实验使用Windows版本的TensorFlow学习框架,采用Anaconda软件包结合Python语言进行程序编写,实验平台使用的CPU为Inter Core i7- 4790 3.6 GHz,Windows7操作系统,运行内存为8 GB。 根据《泥石流灾害防治工程勘察规范》(DZ/T 0220— 2006)[16],通过野外考察和实地勘测,收集雅鲁藏布江中上游的地形地貌、地质构造、地层岩性以及泥石流发生的历史记录,初步选取13个影响因子作为影响泥石流易发性评价的主要评价指标,具体指标及表征意义如表1所示。 表1 指标及表征意义 研究区灾害点的基础数据,主要来源于西藏高原大气环境科学研究所研究人员长年累月的调查与收集,总共统计出有记载的1 778个泥石流地质灾害点。本文采用中国地质调查局《滑坡崩塌泥石流灾害详细调查规范》来划分暴发频率,如表2。 由暴发频率图(图3)可以看出,雅鲁藏布江中上游流域泥石流灾害主要以中易发为主。 图3 研究区域泥石流灾害易发性等级统计 泥石流易发性受孕灾环境的多重因子影响,各类别数据之间存在不平衡现象, 因此,需要弥补少数类样本在信息分布方面的不足。本文使用Borderline-SMOTE算法为少数类样本:不易发、低易发、高易发插值生成新的样本,提高分类器对少数类样本的识别精度。对评价因子进行归一化处理既是模型建立的需要也是为防止不同指标因单位不同,数据存在偏大或偏小问题。最后将训练样本的目标矢量设为(1,0,0,0)、(0,1,0,0)、(0,0,1,0)以及(0,0,0,1),作为易发性的等级,结果如表3所示, 样本数均为1 194。 表3 泥石流易发性等级 依据神经网络的基本原理,三层神经网络已经能够有较好的分类性能。本文使用两层隐藏层,因为在实验过程中发现多一层隐藏层能更快地实现收敛,且准确率更高。输入层根据泥石流易发性评价因子,使用13个神经元。输出层根据待分类类别数,使用4个神经元。实验设置初始的权值与阈值为随机系统值。隐藏层节点数常常使用试凑法确定,使用经验公式(6)获取节点数的取值范围为5~14,使用排列组合的方式,对同一个样本集进行训练,最终选取高准确率对应的节点数。实验基于雅鲁藏布江中上游流域泥石流灾害历史数据集,在迭代次数相同的情况下,不同隐藏层节点数训练后,得到对应的验证集准确率如图4所示。 横坐标为第一层隐藏层节点数,图例不同形状表示第二层隐藏层节点数(如:5、6分别表示第二层隐藏层节点个数为5和6),纵坐标表示分类准确率。分析图4可知,当隐藏层结构为11- 14时,网络准确率能够到达最高值,因此神经网络的结构设为13- 11- 14- 4。 图4 不同隐节点数准确率统计 下面对比研究泥石流灾害历史数据集有无Borderline-SMOTE算法处理对模型分类准确率的影响。 如图5(a)所示,地质数据未经预处理时,网络验证准确率在迭代2 000次之后趋于稳定,迭代时间为12.3 s,此时,训练准确率为94%,但是验证准确率仅85%左右,类别间数据不平衡导致严重过拟合现象。相反,从图5(b)可以看出,经过算法处理后的数据集,进入网络迭代至8 000次左右,网络验证准确率趋于稳定,训练时间较长,为23.5 s,此时训练准确率达96.5%,验证准确率为94.3%,过拟合现象得到明显缓和,可见该重采样算法降低了不平衡数据集对神经网络的影响,使模型更具有普适性。 GA_BP网络在训练时,使用与之前一样的网络结构,即:13- 11- 14- 4。对于GA参数,本文依据前人工作[17-18]以及多次反复实验,选择种初始群规模为Size=20。最大遗传代数Gen=20;交叉概率为Pc= 0.6;变异概率为Pm=0.1。训练过程中,设置最大训练次数为900,验证准确率目标为94%。图6所示为遗传算法优化后的准确率曲线,模型迭代到300次以后趋于稳定,训练准确率高达96%,此时验证准确率为94.03%,运行时间仅为3.25 s。对于神经网络,计算复杂度最直接的性能评价参数可通过收敛速度直观衡量[19]。实验证明,遗传算法的全局搜索能力使其在指定进化次数内优化了网络的初始权值和阈值,与3.3节随机初始化的方式相比较,训练所需要的迭代次数和时间大幅降低。因此遗传算法有利于降低神经网络的计算复杂度,提升收敛速度。 图6 GA_BP准确率曲线 根据已经训练好的网络,设置训练集每个特征数据的调节率为10%,即对其分别做乘以1.1和0.9操作,然后计算每个泥石流影响因子的MIV算法值,并按照MIV绝对值从大到小排序,计算结果如表4所示。 表4 各指标MIV 表4中x2、x4、x5、x6、x8、x9、x10、x11、x12呈现正相关,其余特征为负相关。 据泥石流易发性评价因子从大到小排序,构建包括排序值前1至前13个因子的13种因子组合。将每种组合作为模型的输入,使用上述GA_BP网络对其训练,并对包含955个样本的验证集进行验证,记录模型分类准确率如图7所示。 图7 不同因子组合分类结果 从图7可以看出,评价因子的不同组合对分类准确率影响较大。随着泥石流指标因素的增加,分类准确率值总体上呈上升趋势,在到达一定的个数时,趋于稳定。组合1、2、3的准确率相较之下明显偏低,组合8~13的分类准确率十分接近,其中组合11的分类准确率最高(95.23%),所以选取因子组合为11的序号,结果显示,该方法能够有效优化输入维度,删减冗余信息,提升模型精度。 由于准确率评估在多类不平衡的分类评价中存在一些不足,所以其不适合作为评判算法优劣的标准。AUC方法相较于准确率具有更强的可区分性,能够给出不同类的不同分布情况差别[20]。AUC方法定义为受试者工作特征曲线(ROC)下的面积,其值大小作为评判分类器性能的优劣,其中,ROC曲线绘制为真阳性率(True Positive Rate, TPR)与假阳性率(False Positive Rate, FPR)之间的变化关系。本文采用AUC方法,针对13种影响因子,基于未曾使用的400个泥石流灾害数据集,采用Logistic、BP、GA_BP、XGBoost[21]以及本文模型进行区域泥石流易发性评价,对比测试结果如图8和表5所示。 图8 五种评价模型ROC测试曲线 方法输入维度各类别比例AUC值/%测试时间/sLogistic1386∶50∶241∶2392.420.0512BP1386∶50∶241∶2395.230.0016GA_BP1386∶50∶241∶2396.900.0041XGBoost1386∶50∶241∶2397.850.0018本文方法1186∶50∶241∶2397.950.0020 选取400处泥石流灾害点作为测试样本进行模型检验与比较(表5),分析数据显示,本文模型取得97.95%的AUC值,较传统的Logistic算法提升较大,且处理速度有较大幅度领先;BP和GA_BP模型相比,GA_BP算法有着较高AUC值,但在测试时间上稍慢于BP模型;本文在GA_BP基础上结合MIV算法,优化了输入维度,AUC值提高了1个百分点,灾害易发性评价速度也提升了接近50%;最后与当下较为热门的XGBoost分类模型相比,本文算法在AUC值和处理时间上与其几乎持平。总体来说,本文基于神经网络的区域泥石流易发性评价模型具备良好的分类性能和运行速度。 充分利用地质大数据,基于遗传神经网络,结合Borderline-SMOTE算法和MIV算法建立泥石流主要指标与易发程度关系,提高泥石流易发性评价精度,从中挖掘孕灾环境中的泥石流灾害发生规律,以上研究表明: 1)影响研究区泥石流易发程度的原因主要是不良地质现象、主沟纵坡以及新构造影响。输入指标存在冗余信息:松散物平均厚度与地层岩性,影响模型的分类精度和速度。 2)Borderline-SMOTE算法有选择地对少数类数据进行过采样,能够有效克服已有泥石流历史灾害数据分布不平衡的困难,缓解了模型的过拟合现象;遗传算法优化BP神经网络的权值和阈值,避免了原有网络随机初始化的不足,有效提升了泥石流易发性分类的效率和泛化能力;MIV算法能够从13个特征因子中选择11个特征因子作为模型的输入,降低了模型的输入维度;最后以测试样本进行仿真,较高的AUC值表明系统可以对泥石流易发性进行分类。本文建立的模型对雅鲁藏布江中上游流域泥石流易发性进行分类,能够根据研究区域内孕灾环境的特征,对泥石流易发性作出合理的分类,避免了个人主观因素对泥石流易发性评价的影响,对当地基础设施(如:公路、铁路)建设,具有重要的指导价值。与此同时,本文模型亦存在一些问题值得进一步研究:加入人类活动的相关因子对模型的影响;采用强正则模型解决过采样可能带来的局部过拟合,以提升化性能。2.2 易发性分类方法
2.3 指标因子评价
3 实验与结果检验
3.1 评价因子的选取与数据源

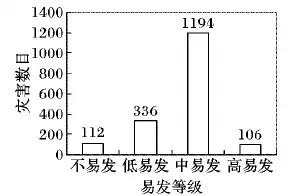
3.2 数据预处理

3.3 确定BP神经网络结构
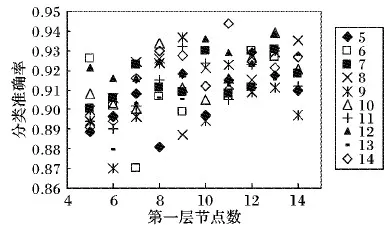
3.4 遗传算法优化神经网络权值和阈值
3.5 计算指标MIV值
3.6 模型检验
4 结语
