规则网格数字高程模型中基于距离与坡度的路径规划算法
2018-12-14张润莲张楚芸奚玉昂
张润莲,张 鑫,张楚芸,奚玉昂
(1.桂林电子科技大学 广西密码学与信息安全重点实验室,广西 桂林 541004; 2.广西高校云计算与复杂系统重点实验室, 广西 桂林 541004;3.重庆电子工程职业学院 电子与物联网学院, 重庆 401331)(*通信作者电子邮箱zhangrl@guet.edu.cn)
0 引言
路径规划是指移动物体基于特定环境,从起点到终点搜索一条符合要求的路径。经典的路径规划算法或寻路算法主要有蚁群算法、遗传算法、Dijistra算法、A*算法、人工势场法和神经网络等。数字高程模型(Digital Elevation Model, DEM)实现了对区域地形表面的数字化表达,是新一代的地形图。在DEM中进行路径规划,道路中的各要素都需要通过计算去发掘,寻路算法需要进行海量的运算,效率低下。
A*寻路算法[1]是一种启发式路径搜索算法,具有运算效率高、搜索空间小的优点,被广泛应用于游戏地图寻路、行军路线规划、车辆越野路径规划、日志模型的校准等方面, 如: 针对栅格地图,文献[2]通过对A*算法的启发性函数改进,提高了四向移动机器人对路径的搜索速度和平滑度;文献[3]基于多种权重加速对栅格图的启发式搜索;文献[4]针对路网,在A*算法基础上,通过权值调整,在多个搜索结果中选择出最短路径;Anisyah等[5]则将A*算法与导航网格的寻路策略相结合,优化船舶的行驶路径;文献[6]基于A*算法进行多径寻由,将路径相似度目标与启发式方法相结合,降低搜索次数;文献[7]将A*算法应用到无线传感器网络,通过优化的最短路径进行数据转发,降低了网络的能力消耗。
目前,学者们已将A*算法应用到针对DEM数据的路径规划中: 文献[8]采用移动窗口和贪婪准则改进A*算法,以在DEM数据中搜索出可达的路径; 文献[9]基于DEM数据,通过计算各栅格的坡度、粗糙度、起伏度识别地形,并采用滑动窗及增量式A*改进算法进行路径规划; 文献[10]利用小波变换进行DEM数据地形处理,以A*算法寻找最短路径; 文献[11]基于DEM数据,将坡度、地表要素等对车辆、步兵行进速度的影响纳入A*算法评价函数的指标,筛选行驶路线; 文献[12]基于3D针对多边形导航网络提出了一种基于多级k-路分割算法的分层方法,并以A*算法进行搜索,提高搜索效率; 文献[13]在火星车自主导航中,通过对于DEM数据的处理,采用A*寻路算法进行路径搜索。
现有针对野外场景中DEM数据的路径规划,更多地是考虑通过对DEM数据的处理,直接应用经典的算法如A*算法或通过局部的算法调整再应用; 然而,将A*算法应用于DEM数据进行路径规划,在野外场景中需要考虑如下问题:1) DEM数据中蕴含了多种刻画地形的地形因子信息,如坡度、坡向、地形起伏度等,在路径规划中,选择哪些地形因子进行评估有待研究;2) DEM数据的分辨率直接影响评价函数的计算结果,因此需要评价函数能够自适应DEM数据的分辨率变化;3) DEM数据随路径规划的区域面积或分辨率的增加呈指数级增长,这使得A*算法的效率急剧下降。
针对上述问题,本文提出一种规则网格DEM数据下基于距离与坡度的改进A*算法(Improved A*algorithm based on Distance and Slope in regular grid DEM data, IA-DS),以距离和坡度作为指标构造新的评价函数进行路径搜索,以地表障碍评判路径的可通行性;根据场景的DEM实际数据,计算评价函数的参数,使得评价函数能够具有分辨率的自适应性;并通过权重的动态调整,提高算法搜索的效率。
1 IA-DS算法的完备性函数设计
A*算法的评价函数为f(n)=g(n)+h(n),其中:g(n)是搜索路径起点到当前迭代点的代价,决定了A*算法能否找到满足条件的路径,被称为完备性函数;h(n)是当前迭代点到终点的估计代价,决定了A*算法的搜索效率,是算法的启发性函数。完备性函数g(n)和启发性函数h(n)共同决定了最终的评价结果。在DEM中,地形的不同会影响人员或车辆的行动,主要地形要素包括坡度、高差与高程、地表障碍等。坡度越大,行动越困难;地表障碍则表明路径难通行。
1.1 基于指数函数的完备性函数设计
在路径搜索过程中,距离影响通行时间,坡度决定通行难度,这两者直接影响路径搜索的结果。针对规则网格DEM数据,在路径规划中,本文以距离和坡度评估、选择通行的节点,并以之构造新的评价函数进行路径选择。距离和坡度量纲不同,取值范围也相差较大,通常坡度取值范围为[0, 90];距离则随起点和终点的不同,其取值范围变化较大。因此,以距离函数和坡度函数构造新的完备性函数g(n)进行评价可以有效避免两者不同量纲和取值范围带来的影响。
在实际应用中,为保证人员或车辆的通行不受影响,需要根据实际情况,设置一个坡度阈值,并在阈值制约下进行路径搜索。在这样的背景下,坡度值可能远小于距离值,坡度和距离对评价结果的影响可能失衡,导致最终的评价结果不合理。假设坡度阈值为S0,为维持距离函数与坡度函数对评价结果影响的平衡性,g(n)中的距离函数与坡度函数需要具备如下性质[14]:
1)当当前坡度大于等于S0时,坡度函数值急剧增加,且大于距离函数值,此时g(n)主要受坡度大小的影响;
2)当当前坡度小于S0时,坡度函数值增长缓慢,其值小于距离函数值,此时g(n)值主要受距离大小的影响。这符合寻路中的距离要求,并最终选择距离最小的节点。
指数函数能满足距离函数与坡度函数的上述性质, 因此,采用指数函数构造坡度函数。在基于规则网格的DEM数据中,距离的计算实际上是指空间路径距离的计算,依据节点间的高程差和平面距离计算得到,因此,以空间路径的计算构造距离函数,则构造的完备性函数g(n)如下:
g(n)=D(n,n-1)+esg(n)
(1)
其中:n为当前节点,sg(n)表示当前节点n的坡度。由于在路径搜索中,算法依次对每一个经过的节点进行评估和筛选,故空间路径的计算仅考虑相邻两点的距离计算,D(n,n-1)表示当前节点n与相邻节点n-1的空间路径距离。
对于当前节点n的坡度sg(n),计算公式如下:
(2)
其中:fx、fy分别为当前节点东西方向和南北方向的高程变化率。在规则网格的DEM数据中,通常采用图1所示的以中心点周围3×3的移动窗格计算fx、fy。
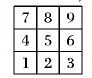
图1 移动窗格
fx、fy的计算方法有二阶差分、三阶不带权差分、简单差分等算法,本文采用文献[15]中提出的三阶不带权差分模型的坡度计算方法,具体如下:
(3)
其中:zi为图1中的相应窗格编号节点的高程值;g为网格间距,是规则网格DEM数据中一个单元格长度,单位为米,其随着DEM数据分辨率的不同而不同。分辨率越高,g越小,其将影响坡度的计算结果。
空间路径的距离计算,依据节点间的高程差和平面距离。设n和n-1为DEM数据中的两个相邻节点,其以经度和纬度标注的大地坐标分别为(Xn,Yn)、(Xn-1,Yn-1),两个节点的高程值分别以H(n)、H(n-1)表示,地球半径常数R=6 371 393 m,以L(n,n-1)表示两个节点间的平面距离,依据文献[16],有:
L(n,n-1)=
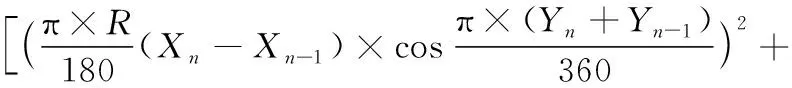
(4)
基于两节点高程差和平面距离,D(n,n-1)计算如下:
D(n,n-1)=
(5)
DEM数据分辨率的变化同样影响空间距离的计算结果。分辨率越高,g越小,|Xn-Xn-1|越小,L(n,n-1)和D(n,n-1)相应减小。
上述计算方法表明,分辨率的变化直接影响g(n)的代价值,最终影响IA-DS算法的评价结果。在实际应用场景中,DEM数据的分辨率各不相同。为获得更好的路径搜索结果,需要设计的算法在寻路过程中能够自适应分辨率的变化。
1.2 g(n)的DEM分辨率自适应优化方法
在指数函数ex中,当变量x=10时,其值接近20 000。对于g(n)来说,此时坡度函数值将远大于距离函数值,这会破坏距离函数与坡度函数对g(n)影响的平衡性。
在指数函数中,底数的变化可以影响函数的值。为维持在坡度动态变化时满足距离函数和坡度函数的平衡性,并适应实际的DEM数据分辨率需求,本节将通过如下方法搜索一个实数a来替换指数函数的底数e。
先以实数a代替指数函数的底数e,g(n)变换如下:
g(n)=D(n,n-1)+asg(n)
(6)
为保证实数a满足距离和坡度函数的平衡性,在距离尽可能小、坡度尽可能大的情况下,建立一个距离与坡度的关联表达式如下:
D(n,n-1)=m×asg(n)
(7)
其中:m为系数,调整坡度与距离的比例;在D(n,n-1)与sg(n)不变的情况下,随着m的加大,a将减小。在m=10时,D(n,n-1)远大于asg(n),此时a已尽可能小,其在坡度变化时,对g(n)的影响也将尽可能降低,这将有利于维持距离函数与坡度函数对评价结果的影响。此时,令m=10;坡度取坡度阈值S0;距离则取平面路径单位距离,其小于等于对应的空间路径单位距离。
为保证实数a适应不同环境DEM数据分辨率的变化,需要搜索的实数a与实际环境的DEM数据相关联。根据上述对距离的取值,以D0表示平面路径单位的平均距离,则式(7)变换如下:
D0=10×aS0
(8)
平面路径单位只包含了南北、东西方向(N,W)与对角线方向(NW),其示意图如图2所示。
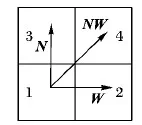
图2 平面路径单位示意图
在规则网格中,东西与南北方向上的平面路径单位距离相等,而对角线方向则相互之间相等。因此,D0的计算就是求南北或东西方向(N,W)与对角线方向(NW)的平面单位路径距离的均值,即D0=[(|N|+|NW|)]/2, 其中:N、W、NW均为方向矢量。
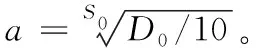
将实数a代入式(6),此时,在g(n)中,D(n,n-1)、sg(n)与a都受DEM数据分辨率的影响。此时,g(n)能够自适应DEM数据分辨率,且满足距离与坡度对评价结果的平衡性。
1.3 路径的可通行性评估
式(6)基于对距离和坡度的计算,实现了从起点到终点可达路径的选择,但在野外实际场景中,还需要考虑各地表要素对路径通行性的影响,如坡度、地形起伏度、地表障碍等。地形起伏度为海拔高度差,可以通过高程差来表示。在DEM数据中,因高程差对路径的影响与坡度的影响一致,而在路径搜索过程中设置了坡度阈值S0,坡度超过S0的节点的g(n)代价值都较高,被排除在选择路径之外,因此,路径的可通行性主要通过地表障碍来评估。
在此,采用模拟地表障碍的方法进行评估。在所选择的数字地图区域中,模拟湖泊、河流和沼泽等不可通行的地表障碍,在对应的DEM数据中,提取地表障碍标识及其坐标。在路径选择中,根据图1所示的移动窗格,对周边节点先判断是否为地表障碍,若是则将其直接加入到Closed列表中,否则计算各节点的代价。
2 IA-DS算法的启发性函数设计
完备性函数g(n)的设计保证了在距离和坡度相互约束下搜索到合适的路径,并适应实际应用环境的分辨率变化。与g(n)一样,h(n)函数同样基于距离和坡度构造。
以n表示当前节点,end为终点;D(n,end)表示当前节点到终点的距离;L(n,end)为当前节点与终点的平面距离;sh(n,end)表示当前节点到终点的坡度;H(n)、H(end)表示当前点与终点的高程。在路径搜索过程中,随着搜索向终点靠近,D(n,end)的值逐步降低,此时,sh(n,end)可有效调整h(n)的大小,避免算法效率过低。新构造的启发性函数h(n)如下:
h(n)=D(n,end)+ash(n,end)
(9)
其中:D(n,end)以式(5)进行计算;a为g(n)中所计算的实数;sh(n,end)的计算公式为sh(n,end)=arctan(|H(n)-H(end)|/L(n,end))。
3 基于权值动态调整的IA-DS优化方法
基于上述构造的g(n)和h(n),IA-DS算法评价函数如下:
(10)
式(10)能够搜索到合适的路径,但随着DEM数据分辨率的提高或搜索路径距离的增加,h(n)可能会逐步降低,IA-DS算法的效率将逐步下降。
从起点开始逐步向终点逼近的搜索过程中,g(n)值和h(n)值是动态变化的。为维持两个函数值对评价结果影响的平衡,提高搜索效率,需要实现权值的动态调整。在此,先列出几个相关概念。
定义1 搜索深度。搜索深度即搜索距离,是当前节点与起点的曼哈顿距离。该距离越大,则当前点离起点越远,即搜索深度越深。以SD(n)表示当前节点n与起点的搜索深度,(X0,Y0)、(Xn,Yn)分别为起点和当前节点在DEM数据中的坐标,则SD(n)=|Xn-X0|+|Yn-Y0|。
以L表示起点与终点的曼哈顿距离,则L=|Xe-X0|+|Ye-Y0|,其中(Xe,Ye)为终点的坐标。
定义2 DEM数据横纵距离。DEM数据横纵距离是指在规则网格DEM数据所对应的区域中,在X和Y方向上的曼哈顿距离之和。以DEMXY表示DEM数据横纵距离,以(XLB,YLB)、(XRB,YRB)、(XRU,YRU)、(XLU,YLU)分别表示DEM数据对应区域的左下角点、右下角点、右上角点、左上角点的坐标,则:DEMXY=|XRB-XLB|+|YLU-YLB|。
由于搜索路径的起点与终点位于DEM数据对应的区域内部,因此,起点与终点的曼哈顿距离L与DEM数据横纵距离DEMXY满足关系:L≤DEMXY。
在IA-DS算法运行初始时期,因搜索深度小,h(n)值较小,为加快搜索速度,可加大h(n)的权值,提高h(n)对评估结果的影响;而随着搜索深度的增加,可逐步降低h(n)的权值,直到两个函数的权值相等,则g(n)和h(n)对评估结果的影响趋于平衡,使其能找到合适的路径,并具有较好的搜索效率。为维持权值的动态变化并满足上述初始时的搜索效率要求,需要设置一个初始权值q0和一个权值增量Δq,它们的取值范围为[0,1],为保证IA-DS算法运行初始时h(n)具有较高的初始权值,并考虑到起点到终点的路径越长,其权值也应与距离有关,令q0∈[b,c],则q0计算方法如下:
q0=b+(c-b)×(L/DEMXY)
(11)
其中:b、c为初始权值的范围下界和上界,L为起点与终点的曼哈顿距离,DEMXY为DEM数据横纵距离。
随着搜索深度的增加,需要以Δq逐步降低q0,维持h(n)和g(n)对IA-DS算法的平衡,则Δq计算公式如下:
Δq=(c-b)×(SD(n)/L)
(12)
其中SD(n)为当前节点n的搜索深度。
将q0与Δq代入式(10)中进行权值调整,则IA-DS算法评估函数如下:
(13)
4 实验及结果分析
4.1 实验环境
本文采用Java语言实现提出的IA-DS算法,并在World Wind平台上进行测试。测试计算机硬件配置为Intel Core i5 2430 2.4 GHz,内存4 GB,操作系统为64位Windows 7。
实验主要测试IA-DS算法的有效性及其在不同DEM数据分辨率下的搜索时间。在有效性方面,测试了IA-DS算法在指定坡度下路径搜索的成功率,并在相同条件下与文献[8]进行了对比测试。在上述实验中,以机器人野外搜索为背景,设定坡度阈值为20度;坡度与距离的比例系数m设置为10;为保证初始权值较大,设b为0.5,c为0.9。
4.2 实验数据准备
在World Wind平台上选取了一块1 000 km2的矩形区域,从区域的左下角起,依次以分辨率0.002°、0.001°、0.000 5°的间隔采样,提取出该区域的高程数据,保存成文件,形成同一区域三种不同分辨率的DEM数据文件。在区域面积固定的条件下,间隔越低,网格个数越多,网格间的距离越短。三种不同分辨率的DEM数据情况如表1所示。
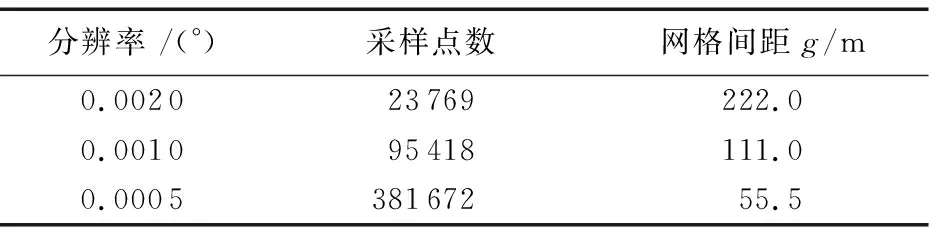
表1 不同分辨率的DEM数据量
在上述所选择的区域,模拟地表障碍,并将其与原始DEM数据叠加,叠加后的该区域高程渲染图如图3所示,其中,左上方粗树枝状为叠加的地表障碍,深色纹路状的区域为高层值较大区域,其他区域为较平坦区域。

图3 所选择区域叠加地表障碍的高程数据渲染图
4.3 实验测试及分析
4.3.1 有效性测试
基于上述选择区域的DEM数据,在地表障碍的附近,设置搜索的起点和终点。在S0为20°时,按照式(13),在3种不同分辨率DEM数据中多次进行路径搜索,IA-DS算法搜索结果如图4所示。
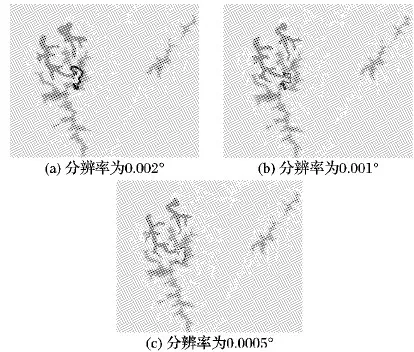
图4 IA-DS在不同分辨率下的搜索路径示意图
图4的搜索结果表明,IA-DS算法能够在坡度约束下搜索到从起点到终点的合适路径。多次搜索,包括在不同计算机上进行搜索,所搜索的路径节点一致,而搜索的具体信息如表2所示。

表2 动态权值IA-DS算法运行结果
由表2数据可知,随着分辨率的变化,所计算的底数a和初始权值都相应变化,表明IA-DS算法具有分辨率的自适应性。同时,分辨率越高,DEM数据量急剧增加,算法搜索的时间开销也激增。在搜索过程中,IA-DS算法能够遵循坡度的限制,搜索到合适的路径。
4.3.2 算法效率测试
实验1 IA-DS算法采用动态权值与未采用动态权值对比测试。
相对于表2,按照式(13)基于动态权值IA-DS算法的测试结果,在同样的坡度阈值和相同的起点与终点下,对比测试了按照式(10)未采用动态权值的IA-DS算法进行路径搜索的结果数据如表3所示。
对比表2和表3的结果可知,基于动态权值IA-DS算法,其通过权值的动态调整,随分辨率的提高,搜索的路径点数量减少,搜索时间较未采用动态权值的IA-DS算法大幅降低,这表明了权值的动态调整有效提高了算法的效率。

表3 未采用动态权值IA-DS算法测试结果
实验2 不同算法的对比测试。
在同样的环境下,对比测试了本文基于动态权值的IA-DS算法和文献[8]算法进行路径搜索的结果。在文献[8]中,其本身并未考虑坡度的限制。因此,在测试中,先测试不对文献[8]进行坡度限制的测试结果。从测试结果中发现,其坡度极大值近40°。此时,对本文的IA-DS算法,设置坡度阈值S0为40°,两种算法的测试结果如表4所示。
在上述测试中,坡度阈值的变化,引起IA-DS算法中底数a的变化。两种算法在同样坡度限制下的对比测试结果表明,IA-DS算法具有更好的搜索效率。
进一步地,对文献[8]增加坡度的限制,测试两个算法均在坡度阈值为20°时的搜索结果,见表5所示。
表4和表5的搜索结果对比表明,在增加或提高了坡度约束后,IA-DS算法与文献[8]的搜索效率都急剧降低,但IA-DS算法通过距离与坡度的约束及动态权值提高启发性函数的影响,其效率优于文献[8],主要原因在于,虽然两种算法都是对A*算法的改进,两种算法的时间复杂度一致;但因两者计算方法的区别,两种算法所走路径有所区别,文献[8]在寻路过程中覆盖的范围更大,其搜索效率相对要低些。

表4 在S0=40°时两个算法的对比测试结果

表5 在S0=20°时两个算法的对比测试结果
5 结语
针对规则网格DEM数据,本文提出一种基于A*算法的改进方法。该方法以距离和坡度作为指标,设计新的完备性函数和启发性函数,并以地表障碍评判路径的可通行性;函数中的参数,根据实际场景的DEM数据来计算,使得设计的评价函数能够自适应DEM数据分辨率的变化;通过权重的动态变化,调整启发性函数的权值,提高算法搜索的效率。实验测试结果表明了本文算法的有效性,它能够自适应DEM数据的分辨率变化,并在坡度约束下搜索到合适的路径。将来的工作中,考虑对基于搜索深度动态权值调整策略作优化,提高算法的效率,并调整搜索路径的偏差。
