基于NARX神经网络的热负荷预测中关键影响因素分析

谢吉洋，闫 冬，谢 垚，马占宇

(1.北京邮电大学 模式识别与智能系统实验室，北京 100876； 2.北京邮电大学 图书馆，北京 100876)(*通信作者电子邮箱mazhanyu@bupt.edu.cn)

0 引言

区域供热(District Heating, DH)，也称为区域集中供热，是当前向建筑供热的最为有效、环境友好和性价比高的供热方法[1], 即便如此，它需要进一步提高供热效率以降低运营成本并提高盈利能力。降低峰值负荷是提高供热效率和节省燃料成本的关键问题。为了降低峰值，了解能源消耗模式并精确预测峰值负荷尤为重要。对于区域供热网络，希望可以根据热力需求，以动态的方式(例如，每1 h或每15 min)调整供热，降低供热成本，达到提高盈利能力的目的, 因此，准确预测热负荷是至关重要的。

许多外部因素对建筑热负荷存在影响，例如气候条件、建筑物特性、时间、社会学参数[2]等。预测模型需要将热负荷与这些影响因素相关联，以确定它们对热负荷的影响程度。气候条件是热负荷预测中较多涉及的一类因素, 其中，环境温度是最重要的气候条件，因为它决定了室内和室外的温差，是热传递的关键驱动力[3-4]。然而，仅考虑环境温度是不够的。为进一步提高热负荷预测的准确性，现有研究已经尝试考虑其他气候条件，例如直接太阳辐射和风速，并且已经认识到二者对建筑物热负荷的影响, 它们对建筑物热负荷的具体影响尚未得到广泛研究，特别是以定量方式[5]。文献[6]使用多元自回归模型(Multiple Autoregressive Model)研究了气候因素与集中供暖系统热负荷的线性相关性；文献[7]讨论了气候因素对室内温度的影响，以间接影响热负荷。

应用于热负荷预测的模型可分为两类：1)物理模型，基于能量守恒定律和热传递原理[8-9]；2)统计模型，基于数据采集和处理技术[2, 10-11]。随着智能仪表和能源网络的完善以及数据采集、传输和存储技术的发展，越来越多的能源数据可以应用于热负荷预测领域，为统计模型开辟了更大的发展空间[12]。基于统计模型的数据分析方法可以帮助研究者从大量数据中提取有价值的信息，进一步用于能源网络管理和算法开发工作[13]。由于统计模型的独特优势，如反映消费者社会行为模式的能力等，其在热负荷预测方面吸引了越来越多的关注。通常，在能源网络中，线性回归(Linear Regression, LR)[3,14-15]、支持向量回归(Support Vector Regression, SVR)[16-17]和神经网络(Neural Network, NN)[18-19]等数据分析方法，已经广泛应用于热负荷预测领域,并显示出良好的预测性能; 同时，文献[2]使用混合高斯模型(Gaussian Mixture Model, GMM)预测多种条件下的建筑物热负荷; 文献[20]使用基于遗传算法优化BP(Back Propagation)神经网络对供暖系统热负荷进行预测。

本文旨在以定量方式讨论直接太阳辐射和风速对建筑物热负荷的影响， 为此，带外部输入的非线性自回归(Nonlinear AutoRegressive with eXogenous input, NARX)神经网络模型将被用于各种气候条件下的热负荷预测。现有研究中，NARX神经网络已应用于短时电力负荷预测[21-22]、长时电力负荷预测[23]和太阳能光伏发电负荷预测[24]等领域。本文结合多种气候因素从能源生产侧对区域供热负荷进行建模预测，其结果可以直接用于优化能源生产，从而达到节省燃料、降低成本的目的。

1 模型描述

1.1 NARX神经网络

NARX神经网络是用于时间序列预测的非线性动态循环网络，是循环神经网络(Recurrent Neural Network, RNN)的一种，由输入层、输出层、反馈层和多个隐含层组成。输入层、隐含层和输出层的结构类似于前馈神经网络(Feed-Forward Neural Network, FFNN)，而它的反馈层连接网络的输入和输出层[23]。在NARX神经网络模型中，反馈层节点的作用是存储上一时刻输出层节点的输出值，可以看作一种时间延迟算子。具有多个隐含层的NARX神经网络的结构如式(1)～(4)所示：

x1(k)=f[w1u(k)+wcxc(k)]

(1)

xi(k)=f[wixi-1(k)];i=1,2,…,s

(2)

xc(k)=y(k-1)

(3)

y(k)=g[ws+1xs(k)]

(4)

其中:s是隐含层层数，u(k)是在时间k时的神经网络输入，xc(k)和xi(k)是反馈层和隐含层的输出，y(k)是输出层的输出，wi是隐含层之间连接的权值矩阵，wc是连接反馈层和隐含层的权值矩阵，f(·)和g(·)是传递函数。NARX神经网络的结构如图1所示。

图1 NARX神经网络的结构

1.2 数据

从供热公司获取到的2008 — 2011年期间(1 461 d)的小时测量数据,包括热负荷、环境温度、直接太阳辐射和风速数据。本文通过实施短时和长时热负荷预测以研究直接太阳辐射和风速数据对热负荷预测性能的影响： 在短时热负荷预测中，2008- 10至2009- 02(5个月)的数据用于模型训练，2009- 03(1个月)的数据用于模型验证，以选择NARX神经网络模型参数；在长时热负荷预测中，2010年(1年)、2009 — 2010年(2年)和2008 — 2010年(3年)的数据分别用于模型训练，2011年(1年)的数据用于模型验证以讨论直接太阳辐射和风速数据对热负荷预测性能的影响。由于工作日和非工作日的热负荷数据的差异性，本文工作的重点放在工作日期间的热负荷预测研究，以达到更高的预测精度，所以在实验过程中只选取工作日数据用于模型训练和验证。

为了评估直接太阳辐射和风速对热负荷预测精度的影响，本文构建了4个数据集用于NARX神经网络模型的训练和测试，详细描述信息见表1。

表1 数据集描述

注：“○”表示该数据集包含该维度数据，“×”表示该数据集不包含该维度数据。

1.3 模型训练

本文训练NARX神经网络用于预测热负荷。在短时热负荷预测中，为了研究滑动窗口长度对热负荷预测性能的影响，连续的2、4或8 h的历史热负荷数据分别组合成为历史热负荷数据向量，并与环境温度等外部因素分别按照表1所描述的形式组成数据集A～D。

在模型训练过程中，本文选择滑动窗口长度的一半作为滑动步长用以更新历史热负荷数据向量。例如，如果选择 4 h作为滑动窗口长度，并且讨论同时引入直接太阳辐射和风速(数据集D)对热负荷预测精度的影响，则滑动步长是2 h，在训练过程中，第一次训练时NARX神经网络的输入u(1)将包含从第1～4 h的历史热负荷数据、第5 h的环境温度、直接太阳辐射和风速数据，同时将第5 h的热负荷数据作为NARX神经网络的理想输出yd(1)；第二次训练时输入u(3)将包含从第3～6 h的历史热负荷数据、第7 h的环境温度、直接太阳辐射和风速数据，同时将第7 h的热负荷数据作为理想输出yd(3)，以此类推直到数据集D中所有数据都被用于模型训练。

同时，为了研究NARX神经网络中的隐含层数对热负荷预测性能的影响，本文选择4和8层作为NARX神经网络的隐含层数并应用于模型训练。如上所述，在短时热负荷预测中讨论训练数据滑动窗口长度和神经网络隐含层数的2个维度，以选择在长时预测中所使用的模型。

NARX神经网络的训练步骤如式(5)～(7)所示：

i=1,2,…,m;j,l=1,2,…,n;

p=2,3,…,s;q=1,2,…,r

(5)

(6)

(7)

其中：ηp(p=1,2,…,s+1)和ηc分别是wp和wc的学习速率；m、n和r分别是输出层、隐含层和输入层节点数；s是隐含层数。

在使用1.2节中的数据集对NARX神经网络模型进行训练前，需要对数据进行预处理。本文使用Z分数(Z-Score)对数据进行标准化处理。对数据集中的数据向量x=[x1,x2,…,xn]的标准化处理方法如式(8)所示：

(8)

1.4 模型验证

为了评估热负荷预测模型性能，本文使用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)和均方根误差(Root Mean Squared Error, RMSE)作为评估标准。MAPE是衡量模型性能的相对指标，它的定义如式(9)所示：

(9)

RMSE是衡量模型性能的绝对指标。RMSE与实际热负荷数据和预测值都具有相同的量纲，这样很容易计算实际热负荷值和预测值之间的绝对误差。RMSE的定义如式(10)所示：

(10)

其中：yi是实际热负荷值，ypi是与真实值相对应的预测值，n是热负荷预测步长。

学生t检验(Student’s t-test)是作出基本统计分布的假设用于确定两组数据是否具有显著差异性的统计假设检验。本文使用具有不同参数或因素(例如滑动窗口长度、隐含层的数量和气候因素等)的热负荷预测模型进行预测，并将计算的MAPE进行t检验；然后判断不同模型的MAPE是否具有相同的平均值以及相同但未知的方差，以确定这些因素是否在提高模型性能中起决定性作用；同时，箱线图(Boxplot)用于可视地描述MAPE的分布情况，包括5个数值点：最小值、下四分位数、中位数、上四分位数和最大值。

2 实验结果

2.1 短时热负荷预测

在短时热负荷预测中，为了研究滑动窗口长度和隐含层数对热负荷预测精度的影响，本文提出6个模型如表2所示。每个模型分别使用表1所描述的数据集A～D进行10次训练和验证，即进行240组实验，以分析短时热负荷预测的误差分布情况。

表2 不同模型对应的滑动窗口长度和隐含层数设置

本文通过对每个模型进行训练和验证，共获得240组实验结果。每个模型得到的实验结果计算所得的MAPE和RMSE的均值和方差如表3和表4所示。本文使用加粗效果突出显示由同一数据集训练的模型的MAPE和RMSE的最小均值和方差。对于每个实验组的预测结果，MAPE的平均值在4%和5%之间，RMSE的平均值在[17,21]。每组实验的预测的MAPE的方差小于1.50E-05，并且大多数RMSE的方差小于2； 同时，时间窗口长度为4 h的NARX神经网络的热负荷预测性能优于具有另两种时间窗口长度的NARX神经网络；而拥有不同隐含层数的NARX神经网络的热负荷预测性能之间差别不大。

表3 短时热负荷预测中MAPE的均值和方差

表4 短时热负荷预测中RMSE的均值和方差

对两组结果的MAPE进行t检验，得到p值(p-value)如表5和表6所示，统计显著性水平为0.05(α= 0.05)。两组结果对应模型之间的滑动窗口长度或隐含层数不同，而其他参数相同，例如，对具有不同隐含层数模型结果的MAPE之间进行t检验，滑动窗口长度应当保持相同。如果计算的p值低于统计显著性水平，则拒绝零假设并接受备择假设(二者具有显著性差异)。

表5 滑动窗口长度为2、4或8 h的模型结果的 MAPE之间的进行t检验的p值

表6 隐含层数为4或8的模型结果的 MAPE之间的进行t检验的p值

使用4个数据集训练得到的模型计算的MAPE的箱线图如图2所示。本文在图2中分别用方框突出显示了由数据集A～D分别训练得到的最佳模型，其MAPE分布最为集中并且具有最小中位数。根据图2，“NARX_4_4”模型在数据集A、C和D上的MAPE均最为集中且具有最小的中位数。而在数据集B上只有“NARX_4_8”模型略好于“NARX_4_4”模型，而其他4个模型均较差。因此，由图2可以得出，“NARX_4_4”模型是最佳模型。

比较具有不同隐含层数的模型结果，具有4个隐含层的模型的MAPE和RMSE分别略小于具有8个隐含层的模型。此外，t检验的所有结果显示统计学上没有显著差异性，这意味着增加神经网络的隐含层数量不是提高热负荷预测精度的有效方式。隐含层数为8层时，NARX神经网络可能过拟合; 同时，当隐含层数增加时，模型的训练时间将成倍数地延长。本文选择拥有4个隐含层的NARX神经网络。

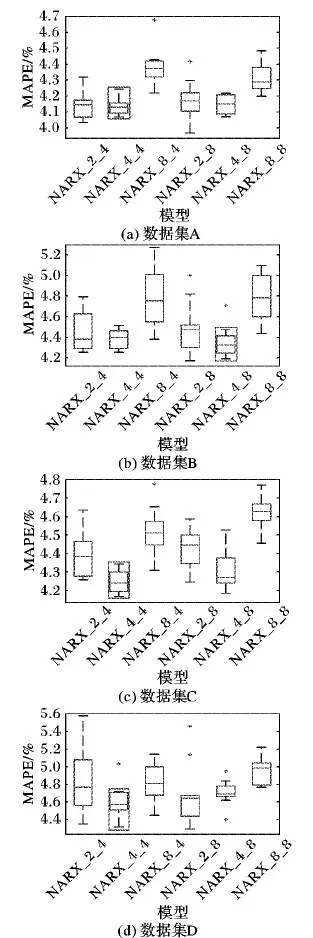
图2 短时热负荷预测中使用4个数据集训练模型的 MAPE绘制的箱线图

比较具有不同滑动窗口长度的模型结果，具有4 h滑动窗口的神经网络的MAPE和RMSE小于具有2或8 h滑动窗口的神经网络；同时，t检验的结果表明2和4 h滑动窗口的分布不具有统计学显著差异性；然而，2和8、4和8 h滑动窗的分布具有统计学显著性差异，所以时间窗口长度为2或4 h的NARX神经网络显著优于时间窗口长度为8 h的NARX神经网络，但前两者并没有显著区别。根据图2中的箱线图，时间窗口长度为4 h的NARX神经网络好于时间窗口长度为2 h的NARX神经网络。本文选择4 h作为滑动窗口长度。

综上所述，NARX神经网络的最佳参数是4 h时间窗口和4隐含层，即“NARX_4_4”模型是最佳模型，此模型将被用于接下来的实验中。

2.2 模型比较

本节通过短时热负荷预测将2.1节中选择的最优NARX神经网络模型“NARX_4_4”与线性回归模型、支持向量回归模型和神经网络模型等多种时间序列预测模型进行比较。其中，线性回归模型选择带有外部输入的整合自回归滑动平均(AutoRegressive Integrated Moving Average with eXogenous input, ARIMAX)模型[25]、支持向量回归模型选择libsvm工具箱实现的epsilon-SVR[26]、神经网络选择前馈神经网络[18]。前馈神经网络的隐含层数和隐含层节点数分别设置为4和15，与NARX神经网络相同。所有模型的时间窗口长度均设置为4 h。在短时热负荷预测中，2008- 10至2009- 02(5个月)的数据用于模型训练，2009- 03(1个月)的数据用于模型验证。

表7展示了每个模型在4个数据集上得到的实验结果计算所得的MAPE和RMSE的均值，每个模型在每个数据集上均重复训练10次。本文使用加粗效果突出显示由同一数据集训练的模型的MAPE和RMSE的最小均值。从表7中可以看出：ARIMAX模型在4个数据集上的热负荷预测性能均为最差，MAPE均大于11%，RMSE均大于43，也就是说线性回归模型并不适合于预测快速变化的小时热负荷数据；同时，epsilon-SVR和前馈神经网络的热负荷预测性能较好，而后者略好于前者；NARX神经网络在4个数据集上的热负荷预测性能均为最优，并且MAPE和RMSE均远小于其他模型。

因此，与其他三种模型相比，NARX神经网络更适合用于热负荷预测。众所周知，当神经网络的隐含层数足够多时，神经网络可以用于拟合任意非线性函数映射，并且具有较强的泛化性能，因此，相对于传统机器学习模型，例如线性回归模型和支持向量回归模型，由于神经网络可以有效拟合快速变化的小时热负荷数据，神经网络的热负荷预测性能较高；同时，由于热负荷数据具有一定的准周期特性，循环神经网络相对于传统的神经网络，例如前馈神经网络可以更好地拟合热负荷数据在时间上的准周期特性，因此，作为循环神经网络的一种，NARX神经网络在热负荷预测性能优于前馈神经网络。上述实验结果和分析表明，NARX神经网络相对于其他模型更适合用于热负荷预测。

2.3 长时热负荷预测

在长时热负荷预测中，2010年(1年)、2009 — 2010年(2年)和2008 — 2010年(3年)的数据分别对“NARX_4_4”模型进行训练，并将训练好的模型命名为“NARX_1”“NARX_2”“NARX_3”；2011年(1年)用于模型验证。每个模型分别使用数据集A～D训练10次，以分析长时热负荷预测的误差分布情况。

每个模型得到的实验结果计算所得的MAPE和RMSE的均值和方差如表8和表9所示。本文使用加粗效果突出显示由同一数据集训练的模型的MAPE和RMSE的最小均值和方差。对于每个实验组的预测结果，MAPE的平均值在6%和8%之间，RMSE的平均值在[15, 18]。每组实验的预测的MAPE的方差小于2.00E-05，并且大多数RMSE的方差小于1。“NARX_3”模型的MAPE在4个数据集上均低于“NARX_1”和“NARX_2”模型，然而，“NARX_3”模型的RMSE与“NARX_2”模型基本相等，且均低于“NARX_1”模型。

表7 多种时间序列预测模型的热负荷性能比较

表8 长时热负荷预测中MAPE的均值和方差

不同模型的MAPE之间的t检验得到的p值如表10所示，统计显著性水平为0.05(α= 0.05)。t检验的结果表明，具有不同训练集大小的模型的MAPE的分布具有统计学显著差异性。

表10 长时热负荷预测中不同模型的MAPE之间的t检验得到的p值

使用4个数据集训练的每个模型的MAPE箱线图如图3所示。由图3可以看出，“NARX_3”模型的MAPE在4个数据集上均最为集中且具有最小的中位数，这表明当使用更多的训练数据来训练模型时，可以获得更高的预测精度和模型稳定性。

图3 长时热负荷预测中使用4个数据集训练模型的 MAPE绘制的箱线图

比较具有不同训练集大小模型的结果，使用越大的训练集来训练热负荷预测模型，MAPE和RMSE越小。当使用1年数据训练模型时，MAPE大于6.7%，RMSE大于16；当使用2年数据训练模型时，MAPE和RMSE分别降低到6.5%和15.5；当使用3年数据训练模型时，MAPE和RMSE分别降低到6.4%和15.3。t检验的结果表明，具有不同训练集大小的模型的MAPE的分布具有统计学显著差异性, 这意味着增加训练集的数量可以有效提高热负荷预测精度，即有效降低MAPE和RMSE。

基于实验结果，本文选择“NARX_3”模型来分析影响因素的对热负荷预测的影响。

2.4 影响因素分析

本文使用数据集A～D的数据训练“NARX_3”模型，并将训练好的模型命名为“NARX_A”“NARX_B”“NARX_C”和“NARX_D”。它们分别使用热负荷和温度数据，热负荷、温度和直接太阳辐射数据，热负荷、温度和风速数据，热负荷、温度、直接太阳辐射和风速数据作为输入，如表11所示。本文只展示2011- 01- 10 — 11的热负荷数据的真实值和预测值(单位：兆瓦特(Million Watt, MW))曲线作为示例，如图4所示。可以从图4中看出，虽然4个数据集上的预测值较为接近，但是数据集D对应的预测值相对于其他数据集的预测值更接近实际热负荷数据，即“NARX_D”模型的误差相对较小，对应的MAPE和RMSE如表11所示。

图4 2011- 01- 10 — 11热负荷数据的真实值和预测值曲线

模型MAPE/%RMSE模型MAPERMSENARX_A6.4916.80NARX_C6.3715.22NARX_B6.4115.63NARX_D6.3514.92

根据实验结果，所有模型都能够反映热负荷变化，MAPE均小于7%，RMSE均小于17，其中“NARX_D”模型具有最佳热负荷预测精度。引入直接太阳辐射和风速对NARX神经网络的性能有积极影响，因为“NARX_B”“NARX_C”和“NARX_D”模型分别具有比“NARX_A”模型更小的MAPE和RMSE，因此，直接太阳辐射和风速都是影响热负荷的重要影响因素。相比之下，由于“NARX_C”模型具有比“NARX_B”模型更低的MAPE和RMSE，引入风速对于提高热负荷预测精度有更大帮助, 这意味着风速是一个更重要的参数; 同时，由于“NARX_D”模型具有最佳的热负荷预测性能，当引入风速和直接太阳辐射可进一步提高模型精度。

绝对百分比误差(Absolute Percentage Error, APE)的分布如图5所示。对于所有模型，大多数APE误差(>60%)在-5%～5%。不过，值得注意的是，尽管“NARX_A”具有最高的MAPE，但APE在-5%～5%的范围内的数据点数也是最多的。同时，还有很多数据点对于热负荷的估计过低。

图5 APE的分布

3 结语

环境温度、直接太阳辐射和风速已被确定为预测建筑物热负荷的关键影响因素。为了了解不同因素的影响，本文将NARX神经网络模型用于区域供热网络中的热负荷预测，引入不同影响因素的数据集进行NARX神经网络训练，并通过多组实验对这些NARX神经网络的热负荷预测性能进行了比较。根据实验结果，可以得出以下结论：

1)NARX神经网络能够用于热负荷预测。本文选择4 h作为滑动窗口长度并且使用4个隐含层的NARX神经网络进行实验。当引入环境温度作为唯一的影响因素时，MAPE小于7%。

2)一般来说，引入风速在内的NARX神经网络的总体MAPE(6.37%)比引入直接太阳辐射(6.41%)更低，并且也拥有较低的RMSE，这意味着风速是一个更重要的影响因素。

3)引入风速和直接太阳辐射能够得到最佳的模型性能(MAPE = 6.35%)，然而，相对于只引入环境温度，同时引入风速和直接太阳辐射对于降低MAPE和RMSE的贡献较小，所以同时引入风速和直接太阳辐射不能有效提高NARX神经网络的模型精度。

出现上述情况可能是由于以下原因：

1)一个因素的对于供热负荷影响已经包含在另一个因素中(例如，温度可能反映风速对热负荷的影响)，因此，不必在分析中包含更多的冗余信息。我们将在以后的研究中进行进一步的验证。

2)对于NARX神经网络，集成多种影响因素有不同的方法。为了进一步改善NARX神经网络，可以采用其他影响因素融合方法。例如，利用分层神经网络的原理，可以分别对多个具有单一因素的NARX神经网络进行训练，然后将这些经过训练的NARX神经网络组合起来，以获得新的模型进行预测。

3)数据不连续性和异常值，包括加性离群值、水平位移等，是影响数据质量的因素，也可能影响热负荷预测的性能[27], 因此，有必要提高获得数据的质量。在未来的工作中，应在模型训练和验证之前对实际热负荷数据的质量进行评估。