多机布阵航路规划问题研究

敬玉平，张雨杭，巩健文，范赵鹏

（海军航空大学，山东烟台264001）

现代反潜战中，声呐浮标搜潜具有速度快、探测区域广、阵型多样化等优点[1]。浮标布阵航路规划是指在满足目标约束条件的基础上为反潜机选择一条最优的航路完成布阵任务。多机布阵航路规划问题本质上是加入约束条件下的多旅行商问题（mTSP），即给定n个浮标点、m架直升机，从指定的相同或不同的位置出发，在布阵时间最短的原则下，求各架直升机的路径。目前，有关多机航路规划的研究基本还是空白，对于多旅行商问题的研究也没有特别有效的算法。mTSP的研究开始于20世纪70年代，刚开始人们致力于采用精确算法进行研究，但由于其运算量随问题规模的扩大而呈指数型增长[2]，研究思路转向了启发式算法或元启发算法，比如Lin-kernighan算法[3]、自组织神经网络[4-5]、遗传算法[6-8]、蚁群算法[9]等。目前，针对mTSP的解决思路大部分是将mTSP转化为单旅行商问题（TSP），再采用TSP的解法来进行处理。转化方法主要是在原编码基础上加入新的虚拟节点，来把整个目标点分割成与旅行商数量相同的几段。本文将根据目标位置的相对位置和离散程度采用聚类算法来将其分割成块。接着根据最长路径最短的原则，按一定的方法将各块分配给各个旅行商，从而将mTSP转化为TSP，再利用模拟退火算法来分别进行路径规划。为了进一步优化规划结果，采用了转移最长路径节点的方法，将路径长度平均化，最后得到了较优的规划结果。

1 问题描述与模型建立

为了方便描述，现将问题简述如下：假设确定参与布阵的直升机集合为{F1,F2,…,Fm}，共m架，位置已知，各自携带的浮标数为N1,N2,…,Nm，记各架直升机的初始位置点的集合为，飞行前准备时间的集合为{t01,t02,…,t0m}，最大航程的集合为{D1,D2,…,Dm}，浮标点共n个，位置记B1,B2,…,Bn。现在要求直升机从初始位置出发，飞过所有浮标点，求最短路径。据此建立模型如下[5]：

式（1）为目标函数，本文研究的多机航路规划问题以布阵时间最短为目标，假设每架直升机的速度相同，则优化目标等同于使各架直升机路径的最大值最小，cij表示的是从点i到点j的路径成本，通常等于i、j两点间距离，因而cij=cji。式（2）为执行任务约束，含义为每个待布设的浮标点必须被访问且只能被访问一次。式（3）是任务可行的必要条件，表示待布设的浮标点数必须不大于各架直升机携带的浮标数量之和。否则，任务无法完成。式（4）表示各架直升机布设的浮标数量应不大于其携带量。

为简化问题，提出假设：①不考虑浮标下落弹道的影响；②不考虑风向、风速对直升机的影响；③每架直升机航速相同且保持匀速；④不考虑飞行前准备时间；⑤不考虑洋流、海深对浮标投放的影响；⑥不考虑飞行安全问题；⑦每架直升机的可留空时间足够长。

2 求解策略及优化方法

一般情况下，可以假设离得近的浮标点更有可能在同一路径之下。在此基础之上，采用聚类算法将所有浮标点按照相对距离和离散程度划分为与直升机数量相同的几类。然后，计算各架直升机到各类之间的相对距离，类的位置可以根据类中所有目标位置的平均值来表示。再根据使布阵时间最短原则，将各类分配给各架直升机，分配方案还需要满足式（4）的要求，即各架直升机负责的浮标数量不应大于其携带量。若不满足要求，还需要对分配方案进行调整。至此，实现了由mTSP到TSP之间的转化。接下来，采用模拟退火算法来对各TSP分别进行路径规划，从而得到一个初步的解。即先分割再规划。对解的评估方法可以采用均衡率这一指标。定义均衡率[10]：

若η接近于1，则任务分配方案是较合理的。若η远小于1，则说明最长路径远大于最短路径。那么，如果能够将最长路径的部分浮标分配给最短路径，则可减少整体布阵时间，故还须根据得到的解的情况在式（4）的约束下进行修正。修正方法主要是：将最长路径的最后一个浮标点取出并放入最短路径的类中，若最短路径对应的浮标任务量已达到最大，则交给次短路径。按这种方法依次尝试，如优化后的分配方案无法实现，则跳出优化的循环。否则，根据优化后新的分配方案重新转入对各架直升机采用模拟退火算法进行航路规划的步骤中。如此循环，直到无法继续优化或迭代次数达到最大为止。流程图如图1所示。

图1 求解策略及优化方法流程图Fig.1 Solution strategy and optimization method diagram

这样，在处理单机航路规划中使每条路径最短，在处理单机航路规划外使各个路径长度更平均，两者结合，便能达到使得最长路径最短的目标。

3 算法简介

3.1 聚类分析

聚类分析又称群分析，适合将多个样本或指标进行定量分类[10]。在聚类分析中，通常采用距离来对样本进行分类，用到的距离计算方法主要包括绝对值距离、欧氏距离、切比雪夫距离和马氏距离等。本文采用欧氏距离。假设Ω表示样本点集，则其计算式为：

针对类与类之间的分类方法，本文采用离差平方和法，若记：

式（8）～（10）中：

定义：

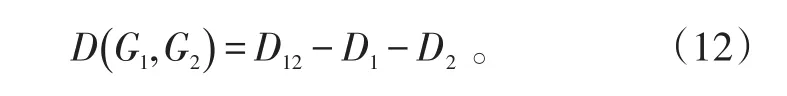
离差平方和法不仅能够使两类内部距离很小的点聚为一类，还能使2类之间充分分离[10-11]。

聚类分析的主要步骤如下[10，12]。

1）利用欧氏距离计算n个样本点两两之间的距离{dij}，建立距离矩阵d={dij}n×n。

2）让各样本自成一类，将对应聚类图中的平台高度为零。

3）采用离差平方和法，计算两类之间的距离，将其中最近的两类合并为一个新类，以这2类的距离作为聚类图中新类的平台高度。

4）重新计算新类与其余各类间的距离。如此时类的数量还没有达到直升机的数量，则返回步骤3）再次执行；若数量已经等于直升机数量，则进入步骤5）。

5）根据计算结果画出聚类图并选出对应的类。

3.2 布阵任务分配

计算每架直升机所在位置与各类之间的距离，类的位置用类中所有元素坐标到飞机位置的最小值来表示，距离计算采用欧式距离。由此可以得到一个m×m的矩阵，m同时表示直升机和类的数量，矩阵的各行表示对于同一架直升机而言，其相对于各类的距离；各列则相应地表示对于同一类而言，其相对于各架直升机的距离。找到每架直升机与各类的最小值，也即每一行的最小值，再从这些最小值中取出最大值，找到这个最大值所对应的行和列，即对应的直升机和类，由此完成第一个任务分配。然后，删去最大值对应的行和列中的所有元素，对矩阵剩余部分仍采用以上方法进行处理，直到全部分配完毕。

3.3 模拟退火算法

模拟退火（Simulated Annealing，SA）算法是由Metropolis等最早提出的，过程分为3个部分。[13-15]

1）加热过程。加热的目的是使粒子的热运动增强，偏离平衡位置。此时粒子的能量较高，可以自由运动，重新排列。

2）等温过程。对于与周围环境交换热量而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行的，当自由能达到最小时，系统达到平衡状态。

3）冷却过程。使粒子热运动减弱（该过程也称退火），系统能量下降，最终得到处于低能状态的晶体。

加温过程对应算法的设定初温，等温过程对应算法的Metropolis抽样过程，冷却过程对应控制参数的下降。这里能量的变化就是目标函数，要得到的最优解就是能量最低态。Metropolis准则是SA算法收敛于全局最优解（指在TSP下的全局最优，而非MTSP）的关键所在，Metropolis准则以一定的概率接受恶化解。这样，就使算法跳离局部最优的陷阱[16-17]。

模拟退火算法的实现过程描述如下[18]。

1）解空间。解空间S可以表示为的所有固定起点的排列集合，每一个排列表示一个可行解，使用蒙特卡洛法得到一个较好的初始解。

2）目标函数。目标函数为路径长度，要求路径长度最短。

3）新解的产生。从上一次迭代得到的解中任意选2个位置（除了出发位置），交换这2个位置之间元素的顺序，变成逆序。

4）代价函数差。代价函数差表示为变换前后2个解之间目标长度的差值。这里用变换后的路径长度减去变换前的路径长度。

5）接受长度。如果代价函数差f小于0，接受新的路径；否则，以概率exp(-f/T)接受新路径。这里由计算机产生一个在[0 ,1]上均匀分布的随机数，若随机数小于或等于exp(-f/T)则接受新解。

6）降温。利用选定的降温系数α进行降温，每次将上一次迭代的温度T用αT来进行更新。

7）结束条件。设定最终温度e，来决定是否结束退火过程。当T＜e时结束退火过程并输出当前结果。否则，返回至第3）步。

其算法流程图如图2所示。

图2 模拟退火算法求解流程框图Fig.2 Simulated annealing algorithm diagram

3.4 优化及分配调整算法

经过前面的步骤可以得到一个较为理想的mTSP解，但考虑到各条路径有长有短，如果将最长路径的一部分分配给较短的路径，则可以进一步优化。优化过程如下：

1）取点。将得到的最长路径的最后一个浮标点取出。

2）放入。在仍有布阵能力的直升机集合中找出路径最短的一架直升机，将取出的浮标点放入其任务区中。

3）重新规划。对形成的新任务分配方案返回至3.3节重新进行航路规划。

4）退出循环。退出循环的条件有3条，任意满足一条即退出循环，得到最终解：①循环次数达到最大；②均衡率达到预定值；③当除去最长路径以外的其他路径对应的直升机的任务量均已达到最大；

4 仿真验证

假设有3架直升机，经纬度坐标见表1所示，携带的浮标数量均为3枚。假设指定的布阵任务为一个圆阵，共8枚浮标，其经纬度坐标如表2所示。

表1 直升机经纬度Tab.1 Plane latitude and longtitude (°)

表2 浮标点经纬度Tab.2 Sonobuoy latitude and longtitude (°)

首先，对上述目标点进行聚类分析，得到的聚类图如图3所示。

聚类分析得到的结果为：第1类的有浮标6、7；第2类的有浮标4、5；第3类的有浮标1、2、3、8。

计算这3个类分别与3架直升机之间的距离，用类中各点到飞机的最近距离来表示，采用欧式距离计算。最后，得到的距离矩阵为：

式中，aij表示第i架直升机与第j类之间的距离，单位为km。

图3 目标点位置聚类图Fig.3 Target point location cluster diagram

根据3.2节中布阵任务分配方法，可知布阵任务分配的结果为：第1架直升机负责第1类浮标；第2架直升机负责第2类浮标；第3架直升机负责第3类浮标。

接下来采用模拟退火算法对3架直升机分别进行路径规划，在同一张图上显示。最后得到的结果如图4所示。详细的数据见表3所示。

图4 路径规划结果图Fig.4 Route planning diagram

表3 路径规划数据结果Tab.3 Route planning data result

由表3数据，结合式（6）可以得到均衡率等于0.766 2，最大长度为16.144 4km。最大长度与最小长度相差较大，且第3架直升机负责的浮标数量为4枚，超过了其布放能力。在此基础之上，采用3.4节所述的优化算法，得到新的路径规划结果如图5所示。详细的数据见表4所示。

图5 优化后路径规划图Fig.5 Route planning result diagram after optimization

表4 优化后路径规划数据结果Tab.4 Route planning data result after optimization

由表4数据结合式（6）可以得到均衡率约等于0.890 5，最大长度为14.445 9km。由图5和表4的结果可知：经过优化处理后，均衡率有所提高，而且最大长度变大。同时，浮标数量的约束条件得以满足。因此，可以认为优化结果是可接受的。

5 结束语

针对多机布阵航路规划问题，本文给出了一种切实可行的算法，通过对任务的分解，能够解决多机航路规划问题中的协同与路径规划问题，在此基础上，又给出了优化的方法。仿真结果显示，经过优化后的结果是可信的，且有较高的效率。但是在航路规划中没有考虑飞行的安全性，布设的方便性，以及气象条件等因素对航路规划的影响。接下来，还需要针对以上几个问题加以改进。