本期试卷参考答案
2018-12-14郭正华
编者的话:同学们在演练的过程中,如果需要更为详细的参考答案,请扫描右边的二维码,关注编辑部的官微“高中数学解题反思”,不但能获悉详细参考答案,还可以另辟蹊径,开拓知识视野,学会解题反思!

空间几何体综合演练A卷参考答案
一、选择题
1.提示:先根据正视图和俯视图还原出几何体,再作其侧(左)视图。应选B。
2.提示:由三视图可知此几何体为一个球切割掉1后剩下的几何体。设球的半径为8 r,则,可得r=2,故表面积。应选A。
3.提示:由几何体的三视图可知,该几何体是一个底面半径为1,高为3的圆锥的一半与一个底面是直角边长为2的等腰直角三角形,高为3的三棱锥的组合体。该几何体的体积应选A。
4.提示:过点A,E,C1的截面为AEC1F(图略),则剩余几何体的侧视图为选项C中的图形。应选C。
5.提示:由题意可知,该几何体的底面为等腰直角三角形,等腰直角三角形的斜边长为2,腰长为2,棱柱的高为2,所以其侧面积S=2×2+22×2=4+42。应选C。
6.提示:由三视图可知,原几何体是一个四棱锥,其中底面是一个上底、下底、高分别为1、2、2的直角梯形,一条边长为x的侧棱垂直于底面,于是其体积为=,解得x=。应选C。
7.提示:根据题意,三棱锥P-BCD的正视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高;侧视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高。故三棱锥P-BCD的正视图与侧视图的面积之比为1∶1。应选A。
8.提示:设圆柱底面圆的半径为r尺,高为h尺。依题意可知圆柱体积为V=πr2h=2000×1.62≈3×r2×13.33,所以r2≈81,即r≈9。所以圆柱底面圆周长为2πr≈54(尺)=5丈4尺。应选B。
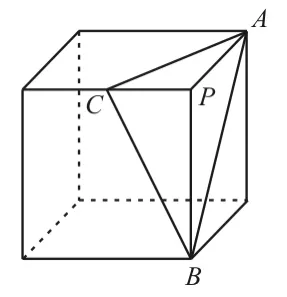
图1
9.提示:根据三视图可知此几何体是边长为2的正方体截去一个三棱锥P-ABC后剩下的部分(如图1所示),所以此几何体的体积为应选D。
10.提示:由三视图可知,该几何体是底面为等腰三角形,其中一条侧棱与底面垂直的三棱锥(SA⊥平面ABC)(图略)。由三视图中的数据可计算得S△SBC=,所 以 S表面积=2+2。应选C。
11.提示:根据所给的三视图可知原几何体是倒放的圆锥。设圆锥的底面半径为R,高为H,水流的速度是v。由题意得vt=πh。当vt>0时,解得h=,这是一个幂型函数。应选B。
12.提示:依题意设球的球心为O、半径为R、△ABC的外接圆半径为r,则=,解得R=5。由πr2=16π,解得r=4。又球心O到平面ABC的距离为 R2-r2=3,因此三棱锥P-ABC的高的最大值为5+3=8。应选C。
13.提示:因为AE=BE,EF⊥AB,所以AF=BF。同理可得EC=ED。又空间四边形ABCD的四个顶点都在同一球面上,所以球心O必在EF上。设该球的半径为R,OE=x,则R2=AE2+OE2=16+x2,R2=CF2+OF2=4+(4-x)2,由此解得R=应选C。
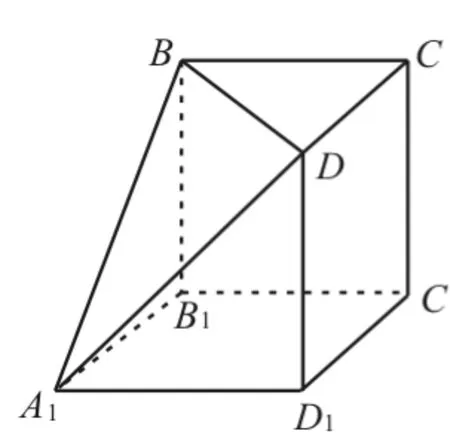
图2
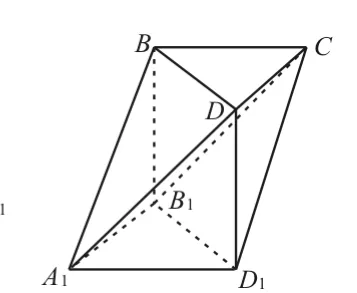
图3
16.提示:由题意可知此三棱锥外接球即为以△ABC为底面、以PA为高的正三棱柱的外接球。因为△ABC的外接圆半径r=,外接球球心到△ABC的外接圆圆心的距离d=1,所以外接球的半径所以三棱锥外接球的表面积S=4πR2=8π。应选C。
二、填空题
17.提示:将直观图还原为平面图形。可知还原后的图形中,O"B"=2,A"B"=,于是可得周长为8。
18.提示:由S原图形=2,可得原平面图形的面积为8。
19.提示:设三棱锥A-BCD的外接球的半径为r,M为正△BCD的中心。因为BC=CD=BD=AB=AC=AD=2,AM⊥平面BCD,所以DM=1,AM=。又OA=OD=r,所以-r)2+1=r2,解得r=。故球O的表面积S=4πr2=
三、解答题
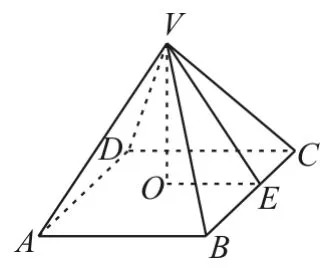
图4
20.提示:由正视图和侧视图的三角形,再结合俯视图可知该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥,如图4。
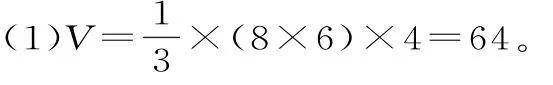
(2)四棱锥的两个侧面VAD、VBC是全等的等腰三角形,取BC的中点E,连接OE,VE,则△VOE为直角三角形,VE为△VBC边上的高,同理侧面VAB、VCD也是全等的等腰三角形,AB边上的高h=5。故S侧=40+24。

图5
21.提示:(1)由三视图可知,该几何体是一个平行六面体(如图5),其底面是边长为1的正方形,高为3。
(2)由三视图可知,该平行六面体中,A1D⊥平面ABCD,CD⊥平面BCC1B1,所以AA1=2。侧面ABB1A1,CDD1C1均为矩形,故该几何体的表面积
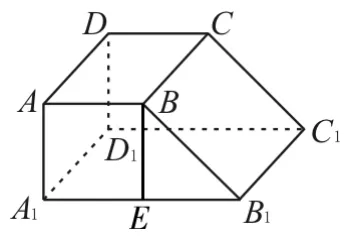
图6
22.提示:(1)直观图如图6所示。
(2)由三视图可知该几何体是长方体被截去一个三棱柱,且该几何体的体积是以A1A,为棱的长方体的体积的。在直角梯形AA1B1B中,作BE⊥A1B1于E,则四边形AA1EB是正方形,可得AA1=BE=1。
在Rt△BEB1中,BE=1,EB1=1,可得BB1=2,故该几何体的表面积S=S正方形ABCD=7+故该几何体的体积V=1×2×1=(m3)。
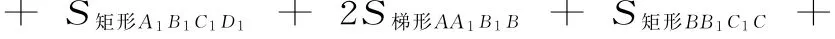
点、直线、平面之间的位置关系综合演练B卷参考答案
一、选择题
1.提示:直线l与平面α斜交时,在平面α内不存在与l平行的直线,A错误。l⊂α时,在平面α内不存在与l异面的直线,D错误。l∥α时,在平面α内不存在与l相交的直线,B错误。无论哪种情形在平面α内都有无数条直线与l垂直。应选C。
2.提示:在空间中,若a⊥b,a⊥c,则b,c可能平行,也可能相交,还可能异面,并且相交或异面时不一定垂直,所以①②错误。③显然成立。也可以构造长方体或正方体模型来快速判断,①②错误,③正确。应选B。
3.提示:当n=2时,满足条件。当n=3时,为正三角形,满足条件。当n=4时,为正四面体,满足条件。当n=5时,为四棱锥,侧面为正三角形,底面为菱形且对角线长与边长相等,这不可能存在。所以正整数n的取值至多等于4。应选B。
4.提示:由AB⊂γ,M∈AB,可知M∈γ。由α∩β=l,点M∈l,可知点M∈β,所以M在γ与β的交线上。同理可知,点C也在γ与β的交线上。应选D。
5.提示:①若a与b是异面直线,则c至少与a,b中的一条相交,①正确。②当平面α⊥平面β时,若b⊥c,则b⊥平面α,此时不论a,c是否垂直,均有a⊥b,②错误。③当a∥b时,则a∥平面β,由线面平行的性质定理可得a∥c,③正确。④当b∥c时,若a⊥b,a⊥c,则a与平面β不一定垂直,此时平面α与平面β也不一定垂直,④错误。应选C。
6.提示:a,b是互不垂直的两条异面直线,把它放入正方体中,容易确定A不正确。由l∥a,且l⊥b,可得a⊥b,与题设矛盾,B不正确。由a⊂α,且b⊥α,可得a⊥b,与题设矛盾,D不正确。应选C。
7.提示:在△C1DB中,MN∥BD,故C正确。因为CC1⊥平面ABCD,所以CC1⊥BD,所以MN与CC1垂直,A正确。因为AC⊥BD,MN∥BD,所以MN与AC垂直,B正确。因为A1B1与BD异面,MN∥BD,所以MN与A1B1不可能平行,D错误。应选D。
8.提示:对于A,平行于同一平面的两条直线可能相交,可能平行,也可能异面,A不正确。对于B,m∥n,m∥α,则n∥α或n⊂α,B不正确。对于C,利用垂直于同一直线的两个平面平行,可知C正确。对于D,因为垂直于同一平面的两个平面的位置关系是相交或平行,D不正确。应选C。
9.提示:若α⊥β,m⊂α,n⊂β,则m与n相交、平行或异面,A错误。因为m⊥α,m∥n,所以n⊥α,又因为n∥β,所以α⊥β,B正确。若m⊥n,m⊂α,n⊂β,则α与β的位置关系不确定,C错误。若α∥β,m⊂α,n⊂β,则m∥n或m,n异面,D错误。应选B。
10.提示:对于A,若l∥α,l∥β,则α∥β或α与β相交,A错误。易知B正确。对于C,若α⊥β,l⊥α,则l∥β或l⊂β,C错误。对于D,若α⊥β,l∥α,则l与β的位置关系不确定,D错误。应选B。
11.提示:A中,因为CD∥AF,AF⊂平面PAF,CD⊄平面PAF,所以CD∥平面PAF成立。B中,因为ABCDEF为正六边形,所以DF⊥AF,又PA⊥平面ABCDEF,所以PA⊥DF,而PA∩AF=A,所以DF⊥平面PAF成立。C中,因为CF∥AB,AB⊂平面PAB,CF⊄平面PAB,所以CF∥平面PAB。D中CF与AD不垂直。应选D。
12.提示:若α∥β,则m∥n,这与m、n为异面直线矛盾,A不正确。α与β相交,将已知条件转化到正方体中,易知α与β不一定垂直,但α与β的交线一定平行于l,从而排除B,C。应选D。
13.提示:对于C项,由α∥β,a⊂α可得a∥β,又b⊥β,得a⊥b。应选C。
14.提示:对于①,当a∥M,b∥M时,则a与b平行、相交或异面,①为真命题。对于②,b⊂M,a∥b,则a∥M或a⊂M,②为假命题。对于③,a与b相交、平行或异面,③为假命题。对于④,由线面垂直的性质,知④为真命题。应选A。
15.提示:对于 A,墙角的三个墙面α,β,γ满足条件,但γ与β相交,故A错误。m⊂α,n⊂β,且m,n平行于α,β的交线时符合B中条件,但α与β可以相交,故B错误。由m∥n,m⊥α可推出n⊥α,结合n⊥β可推出α∥β,故C正确。由D中的条件得α与β可能平行也可能相交,故D错误。应选C。
16.提示:对于①,两条平行线中有一条与一平面垂直,则另一条也与这个平面垂直,①正确。对于②,直线l可能在平面α内,故②错误。对于③,三条交线除了平行,还可能相交于同一点,故③错误。对于④,由α∩γ=n知n⊂α且n⊂γ,由n⊂α且n∥β,α∩β=m,得n∥m,同理n∥l,④正确。应选B。
17.提示:取AC的中点为G。易知SG⊥AC,BG⊥AC,故AC⊥平面SGB,可知AC⊥SB。因为SB∥平面DEFH,SB⊂平面SAB,平面SAB∩平面DEFH=HD,所以SB∥HD。同理可得SB∥FE。由D,E分别为AB,BC的中点,可知H,F也为AS,SC的中点,从而得HFACDE,所以四边形DEFH为平行四边形。又AC⊥SB,SB∥HD,DE∥AC,所以DE⊥HD,所以四边形DEFH为矩形,其面积S=HF·HD=。应选A。
18.提示:因为AB⊥AC,BD⊥AC,AB∩BD=B,所以AC⊥平面ABD。又AC⊂平面ABC,所以平面ABC⊥平面ABD,所以点D在平面ABC内的射影H必在直线AB上。应选A。
19.提示:由D1P⊥PC,DD1⊥PC,且D1P∩DD1=D1,可得PC⊥平面DD1P,所以PC⊥DP,即点P在以CD为直径的圆上。又点P在AB上,则AB与圆有公共点,即0<AD≤CD=2。应选B。
20.提示:因为平面PAC⊥平面PBC,平面PAC∩平面PBC=PC,又AC⊂平面PAC,且AC⊥PC,所以AC⊥平面PBC。而BC⊂平面PBC,所以AC⊥BC,可知点C在以AB为直径的圆上,即点C的轨迹是一个圆,但要去掉A,B两点。应选D。
21.提示:因为截面PQMN是正方形,所以MN∥QP。又PQ⊂平面ABC,MN⊄平面ABC,则MN∥平面ABC。由线面平行的性质知MN∥AC。又MN⊂平面PQMN,AC⊄平面PQMN,则AC∥截面PQMN。同理可得MQ∥BD。又MN⊥QM,则AC⊥BD,故A,B正确。因为BD∥MQ,所以异面直线PM与BD所成的角等于PM与QM所成的角,即为45°,D正确。应选C。
二、填空题
22.提示:①中的直线b与平面α也可能相交,故①不正确。由线面平行的性质可得②正确。由面面平行的性质可得③正确。答案为①②③。
23.提示:由线面垂直的性质定理可知①是真命题,且垂直于同一直线的两平面平行也是真命题,①是“可换命题”。因为垂直于同一平面的两平面可能平行或相交,所以②是假命题,不是“可换命题”。由公理4可知③是真命题,且平行于同一平面的两平面平行也是真命题,③是“可换命题”。因为平行于同一平面的两直线可能平行、相交或异面,故④是假命题,即④不是“可换命题”。答案为①③。
24.提示:①a,c可能相交、平行或异面。②a,c可能相交、平行或异面。③正确。④a,c可能相交、平行或异面。答案为③。
25.提示:把四面体ABCD放入长方体(图略)中进行判断。显然命题①错误。对于②,因为四个面对应的三角形的三边分别对应相等,即它们为全等的三角形,所以②正确。对于③,当四面体ABCD为正四面体时,夹角之和等于180°,③错误。对于④,因为每组对棱中点的连线分别与长方体的棱平行,且都经过长方体的中心,所以④正确。命题⑤显然成立。答案为②④⑤。
26.提示:由题意知AC⊥平面SBC,故AC⊥SB,①正确。根据SB⊥AC,SB⊥AB,可得SB⊥平面ABC,平面SBC⊥平面SAC,②③正确。取AB的中点E,可证得CE⊥平面SAB,故CE的长即为点C到平面SAB的距离,即为a,④正确。
三、解答题
27.提示:(1)在平面PBC内作NH∥BC交PB于点H,连接AH。在△PBC中,NH∥BC,NH=C=1,AM=AD=1。又AD∥BC,所以NH∥AM且NH=AM,可知四边形AMNH为平行四边形,可得MN∥AH。又因为AH⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB。
(2)连接AC,MC,PM,平面PAN即为平面PAC。设点M到平面PAC的距离为h。由题意可得,所以·PA,即43h=2×4,所以h,可知点M到平面PAN的距离为

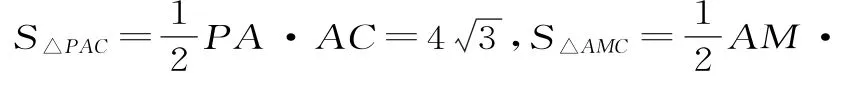
28.提示:(1)设正方形ABCD的对角线AC与BD交于点O,连接FO。由题意知EF=OC=1,因为EF∥AC,所以四边形CEFO为平行四边形,所以CE∥OF。
又CE⊄平面BDF,OF⊂平面BDF,所以CE∥平面BDF。
(2)因为平面ABCD⊥平面ACEF,平面ABCD∩平面ACEF=AC,FA⊥AC,故FA⊥平面ABCD。连接EO,易知四边形AOEF是边长为1的正方形,所以EO⊥平面ABCD,则EO⊥BD。
所以△BDE为等腰三角形,BD=2BO=2OC=2,BE=DE==2。
因为BD2=BE2+DE2,所以BE⊥DE。同理,在△BEF中,BE⊥EF。
又因为DE∩EF=E,所以BE⊥平面DEF。
29.提示:(1)在正四棱柱ABCDA1B1C1D1中,连接BD交AC于N,连接MN。因为ABCD为正方形,所以N为BD的中点。
在△DBD1中,因为M为DD1的中点,所以BD1∥MN。
又因为MN⊂平面AMC,BD1⊄平面AMC,所以BD1∥平面AMC。
(2)因为ABCD为正方形,所以AC⊥BD。因为DD1⊥平面ABCD,所以DD1⊥AC。因为DD1∩BD=D,所以AC⊥平面BDD1。又因为BD1⊂平面BDD1,所以AC⊥BD1。
1点时,平面A1PC1∥平面AMC。证明如下:
因为AA1∥CC1,且AA1=CC1,所以四边形AA1C1C是平行四边形,所以AC∥A1C1。取CC1的中点为Q,连接MQ,QB。
因为M为DD1中点,所以MQ∥AB,且MQ=AB,所以四边形ABQM是平行四边形,可知BQ∥AM。
同理可得,BQ∥C1P,所以AM∥C1P。又因为A1C1∩C1P=C1,AC∩AM=A,所以平面A1PC1∥平面AMC。
