基于深度信念网络伪量测建模的配电网状态估计

孙国强，钱 嫱，陈 亮，卫志农，臧海祥，王晗雯，黄 强

(1. 河海大学 能源与电气学院，江苏 南京 210098；2. 国网江苏省电力公司电力科学研究院，江苏 南京 211103)

0 引言

近年来，分布式间歇性能源的接入给配电网运行与控制带来了极大挑战。为支撑配电网经济运行、故障定位及恢复、需求侧管理等一系列高级应用，亟需研究状态估计技术实时感知配电网的运行状态[1-3]。

与输电网相比，配电网量测配置难以保证可观性，因此需要增加伪量测以提高配电网的量测冗余度，保证状态估计的可解性。与实时量测相比，伪量测误差较大，导致状态估计结果精度下降，因此有必要研究获得高精度伪量测的方法。文献[4]提出了2种伪量测建模方法：基于相关性以及基于负荷概率密度函数伪量测建模。文献[5]基于典型负荷曲线以及智能电表采集的用户负荷数据，利用线性规划法确定无监测的用户负荷曲线。文献[6-8]利用超短期负荷预测实时跟踪网络负荷的变化，以获得负荷节点的伪量测功率，一定程度增强了系统的可观测性，但该超短期负荷预测结果的精确度较低，可能使状态估计结果偏离真实状态。文献[9-10]利用人工神经网络ANN(Artificial Neural Network)进行伪量测建模，提高了配电网状态估计的计算精度，虽然ANN可以模拟人的大脑结构进行非线性映射，但当神经网络的层数增加时，其预测性能降低。近年来，深度学习理论作为研究热点[11]，具有很强的学习能力，擅长处理高维、非线性、大规模数据回归与分类问题，因此其在基于负荷预测的伪量测建模领域具有潜在应用前景。深度信念网络DBN(Deep Belief Network)是应用于深度学习训练的非卷积模型之一，通过逐层训练受限玻尔兹曼机RBM(Restricted Boltzmann Machine)获得网络参数。DBN的引入使得深度学习模型的优化得以简化，推进了深度学习的大规模应用。

除了伪量测，配电系统还有大量的虚拟量测，即零注入节点的功率量测。虚拟量测值为0，不需要通过量测设备获取，对于提高状态估计精度至关重要。传统处理虚拟量测的方法有大权重法[12-13]和拉格朗日乘子法[14-15]。由于配电线路R/X比值较大，大权重法的计算过程中信息矩阵病态的可能性大幅增加。拉格朗日乘子法处理零注入约束能够严格保证零注入节点功率为0，但计算效率偏低。文献[16]将零注入约束转化为模型的线性约束，使得状态估计求解过程更加简便。

针对配电网实时量测数据难以满足状态估计需求的问题，本文首先提出基于DBN的伪量测建模方法，将多种类型负荷数据输入DBN进行训练得到伪量测模型，再利用高斯混合模型[17]GMM(Gaussian Mixture Model)计算相应的权重。同时为避免虚拟量测与伪量测权重相差过大引起数值稳定性问题，以线性约束的形式处理虚拟量测，并采用改进等效电流量测变换法[18]进行线性状态估计。仿真结果表明，本文方法通过基于DBN的伪量测建模有效提高了状态估计精度，同时线性约束确保了零注入节点的功率严格为0，又能避免大权重法易导致的信息矩阵病态问题，具有良好的实用价值。

1 配电系统状态估计基本原理

当系统网络结构、参数、量测数据给定时，量测量和系统状态变量之间的非线性关系可表示为：

z=h(x)+v

(1)

其中，z为量测量向量；x为状态变量向量；v为量测误差向量；h(x)为描述量测量z和状态量x之间关系的非线性量测函数。

基本加权最小二乘法的目标准则为量测函数的计算值和所对应量测值之差的加权平方和最小，其目标函数为：

minJ(x)=[z-h(x)]TW[z-h(x)]

(2)

其中，W为量测权重矩阵。利用牛顿法迭代求解式(2)，迭代方程组形式为：

Δxl=G-1(xl)HT(xl)R-1[z-h(xl)]

(3)

xl+1=xl+Δxl

(4)

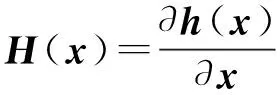
2 DBN基本原理

DBN是深度学习的生成模型之一，由多层RBM堆叠而成。RBM作为一种有效的特征处理方法，能够求解电力系统高维、复杂、非线性问题[19]。本文采用DBN对节点的伪量测功率进行建模以获得精度较高的伪量测。

2.1 RBM

RBM是由可见层和隐含层构成的对称、无自反馈的随机神经网络模型，层内神经元无连接，层间神经元通过权重全连接，其典型拓扑结构如图1所示。图中s为可见层，表示观测数据；g为隐含层，相当于特征提取器；W为两层之间的连接权重。网络中神经元只有激活、未激活2种状态，通常用二进制数1和0表示。

图1 RBM典型拓扑结构Fig.1 Typical topological structure of RBM

RBM是一种基于统计力学提出的能量模型，令n、m分别为可见层及隐含层神经元的个数，si、gj分别为可见层第i个神经元的状态以及隐含层第j个神经元的状态，状态(s,g)确定的RBM系统所具有的能量可表示为：

(5)

其中，θ={ai,bj,Wij}为RBM的参数，数值可通过训练得到。当参数确定时，可以得到给定状态的联合分布概率：

(6)

其中，Z(θ)为归一化因子。由于隐含层各神经元的激活状态是相互独立的，当可见层各神经元的状态给定时，隐含层第j个神经元的激活概率为：

(7)

同理，当隐含层各神经元的状态给定时，可见层第i个神经元的激活概率为：

(8)

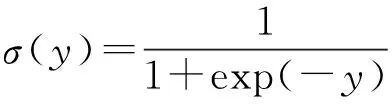
2.2 DBN

DBN是由Hinton等人提出的一种高效学习的深度网络，用于处理高维、大规模数据问题。DBN的发展应用开启了当前深度学习研究的浪潮。RBM不同层数对伪量测建模精度具有直接影响，经过多次实验比较，本文建立2层RBM网络结构的DBN模型，其结构如附录中图A1所示。

在伪量测建模时首先对DBN进行训练，目的是确定连接权重与神经元偏置。训练过程包括预训练和反向微调两部分。预训练过程首先输入负荷历史值、气象信息、日期类型等数据，采用无监督贪心算法训练第一个RBM，完成后将该RBM隐含层输出作为后一个RBM的输入并对其进行训练。反向微调过程采用误差反向传播BP(Back Propagation)算法对参数进行微调，该反向微调过程与BP神经网络的训练原理相同，因此DBN最后一层为单层BP神经网络。

3 基于DBN伪量测建模的改进等效电流量测变换法状态估计

本文算法分为2个部分：采用DBN对节点的伪量测功率进行建模，利用高斯混合模型计算相应的伪量测权重；同时，由于配电网含有虚拟量测，提出采用线性约束处理虚拟量测的方法，建立改进的等效电流量测变换法状态估计模型。

3.1 伪量测建模

本文伪量测为负荷节点的有功功率和无功功率。负荷类型包括工业负荷、居民负荷、商业负荷及其他负荷，基本覆盖了母线负荷的基本特性，具有广泛适用性。

采用DBN对节点的伪量测功率进行建模时，输出变量为待预测日负荷L(d,t)，输入变量为对输出负荷具有较大影响的历史负荷、温度、日期类型。详细的输入变量如表1所示。其中，下标(d，t)表示第d天第t时刻，L(d-1,t-1)为对应前一天前一时刻的负荷值(采样间隔为15 min)；T(d,t)为第d天第t时刻的温度；Dtype为日期类型，分别以数字1—7代表星期一至星期日。

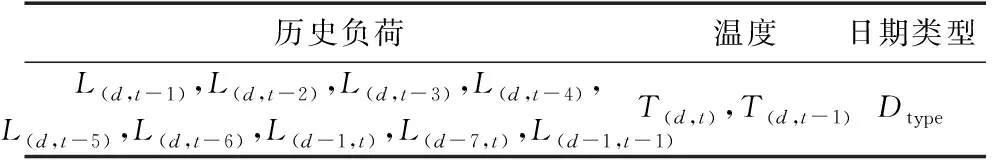
表1 伪量测建模的输入变量Table 1 Input variables of pseudo measurement modeling

将DBN训练得到的一年的负荷节点注入功率误差输入GMM，通过边缘密度函数分析可以得到相应时刻的伪量测误差，从而求取伪量测权重。

3.2 基于等效电流量测变换分离虚拟量测

通过等效电流量测变换可将非线性状态估计转换为线性状态估计，便于分离虚拟量测并采用线性约束形式对其进行处理。本文对DBN进行训练得到伪量测模型后，将实时量测、伪量测、虚拟量测输入改进等效电流量测变换法配电网状态估计器中。实时量测包括部分支路有功功率量测、无功功率量测以及电流幅值量测；虚拟量测为零注入节点的功率量测。

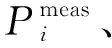
节点注入功率量测等效变换公式为：

(9)

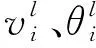
同理可得支路功率量测等效变换公式为：

(10)

支路电流幅值量测等效变换公式为：

(11)

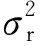
(12)

(13)

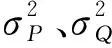
由于本文的状态变量为节点电压相量的实部和虚部，经过等效电流量测变换之后，等效量测Z与直角坐标下的电压V存在以下线性关系：

Z=HV

(14)

等效量测Z中含有虚拟量测Z0和非虚拟量测Zn两部分，基于上式可分离出虚拟量测并以线性约束形式进行处理。将节点电压V分为零注入节点电压X0和非零注入节点电压Xn。则式(14)可以写为：

(15)

分离出上式中的虚拟量测部分，可得虚拟量测的线性约束形式以及剩余非虚拟量测表达式分别为：

Z0=H00X0+H0nXn

(16)

Zn=Hn0X0+HnnXn

(17)

虚拟量测值Z0=0，求解式(16)可得零注入节点电压X0：

(18)

将式(18)代入式(17)中，可得非零注入节点电压Xn与非虚拟量测Zn的关系：

(19)

显然矩阵A为常数矩阵。

根据式(18)和式(19)，求解节点电压X0、Xn是含等式约束的加权最小二乘法优化问题，其模型为：

(20)

利用牛顿法迭代求解上式，迭代方程组形式为：

(21)

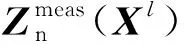
(22)

(23)

(24)

(25)

由上式可知，每次迭代不必重新求解线性量测函数Zn(Xl)的值，计算简便，效率更高。式(18)中求解零注入节点电压不需要赋予虚拟量测权重，避免了信息矩阵病态问题的出现。

4 算例仿真

本文以IEEE 13节点系统及我国某实际地级市35节点配电网(记为C35)为测试算例，其网络接线图分别如附录中图A2、图A3所示。将本文算法与基于BP神经网络伪量测建模状态估计算法及考虑零注入约束的传统大权重法进行比较，验证本文所提算法的有效性。实时量测数据是由潮流真值与服从高斯分布的随机噪声叠加而成，虚拟量测为零注入节点的功率量测。本文算法由MATLAB R2014a编程实现，CPU主频为3.2 GHz，RAM为4 GB。

4.1 伪量测模型测试

本文通过DBN对工业负荷、居民负荷、商业负荷及其他负荷的有功功率及无功功率进行建模。DBN训练过程即是对负荷变化趋势的学习，几类负荷的有功功率变化曲线如附录中图A4所示。为验证DBN伪量测建模的有效性，将其输出结果与基于BP神经网络伪量测建模的输出结果进行比较。

为便于对建模结果进行定量分析，本文采用平均相对误差作为衡量2种不同伪量测建模方法精确度的指标：

(26)

(27)

假设IEEE 13节点系统中节点2、5、8、11的负荷类型分别为工业负荷、居民负荷、商业负荷以及其他负荷。这4个节点a相负荷通过DBN以及BP神经网络建模，输出结果的平均相对误差如图2所示。

图2 DBN与BP神经网络伪量测建模结果对比Fig.2 Results comparison of pseudo measurement modeling between DBN and BP neural networks

根据图2可知，DBN对各个节点负荷建模输出结果的平均相对误差均低于BP神经网络，因此DBN的预测精确度较BP神经网络有明显的改善。

对配电网进行状态估计的周期一般为15 min，而DBN对各个节点负荷建模平均运行时间为68 s，在目前的普通台式机基础上不同负荷的训练可在服务器上并行运算，因此各类负荷在状态估计周期内有足够的时间训练，满足工程应用需求。且短期内若无负荷的不正常剧烈波动，DBN网络无需重复训练，所以DBN的时间性完全能满足配电网状态估计的需求。

4.2 基于2种神经网络伪量测建模状态估计测试

本文在伪量测模型的基础上进行配电网三相状态估计。节点三相电压相角初值δABC=[0，-2/3π,2/3π]，三相电压幅值初值vABC=[1,1,1]p.u.，三相电压实部和虚部初值可由坐标变换得到。伪量测由本文DBN、BP神经网络这2种伪量测模型建立，其标准差通过高斯混合分布拟合的误差分布确定。实时量测中支路功率量测标准差为真值的5%，支路电流幅值量测标准差为真值的3%。考虑到实际配电网中电压幅值量测很少，本文的实时量测中无电压幅值量测，虚拟量测标准差为0.1%。

将基于DBN伪量测建模状态估计结果与基于BP神经网络伪量测建模状态估计结果相比较以验证本文模型的可行性及优越性。

本文采用平均绝对误差和最大绝对误差作为衡量基于2种伪量测建模状态估计精度的指标：

(28)

(29)

(30)

(31)

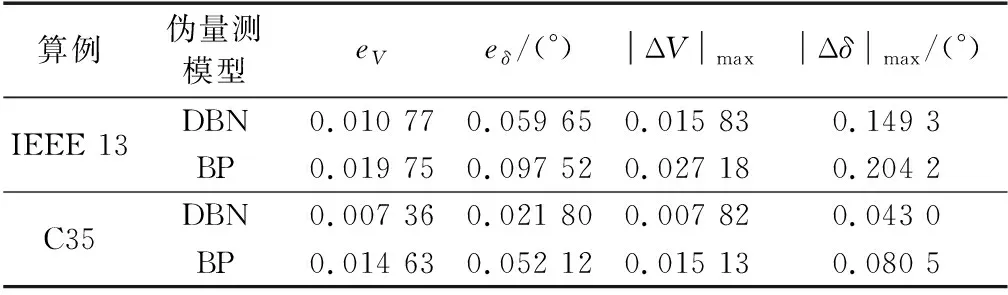
表2 基于2种神经网络伪量测建模的状态估计结果Table 2 State estimation results based on pseudo measurement modeling using two neural networks

由表2可知，基于DBN伪量测建模的配电网状态估计电压幅值和电压相角的平均绝对误差、最大绝对误差均小于基于BP神经网络伪量测建模的配电网状态估计。可见，与基于BP神经网络伪量测建模相比，基于DBN伪量测建模状态估计结果更加精确。

4.3 虚拟量测处理测试

处理零注入约束时，传统大权重法不能严格保证零注入节点功率为0且可能出现信息矩阵病态问题。为了验证本文以线性约束形式处理虚拟量测能够避免以上问题的出现，在伪量测模型基础上分别用改进等效电流量测变换法(记为算法1)和传统大权重法(记为算法2)进行状态估计。2种方法的伪量测均由DBN建模得到。量测配置与4.2节相同。得到的迭代次数、计算时间，以及虚拟量测节点功率绝对值之和

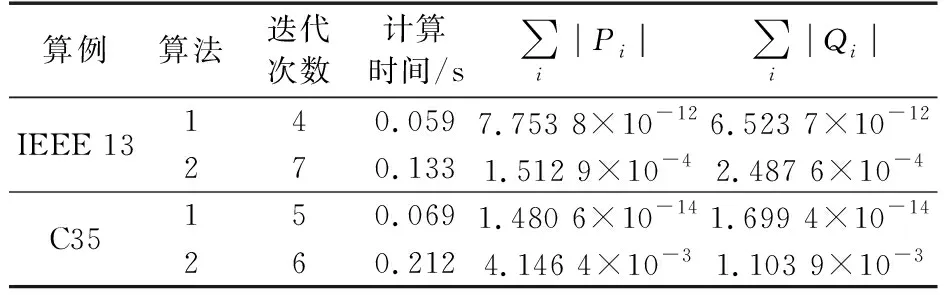
表3 2种算法状态估计结果Table 3 State estimation results of two algorithms

由表3可知，本文算法迭代次数较大权重法更少，且因为雅可比矩阵为常数，计算速度得以提升；零注入节点注入功率绝对值之和远小于大权重法，保证了零注入约束严格满足。

传统大权重法中，虚拟量测权重与伪量测权重相差过大可能引起数值稳定性问题，对于C35节点系统，2种方法信息矩阵条件数的对数值随迭代次数变化曲线如图3所示。

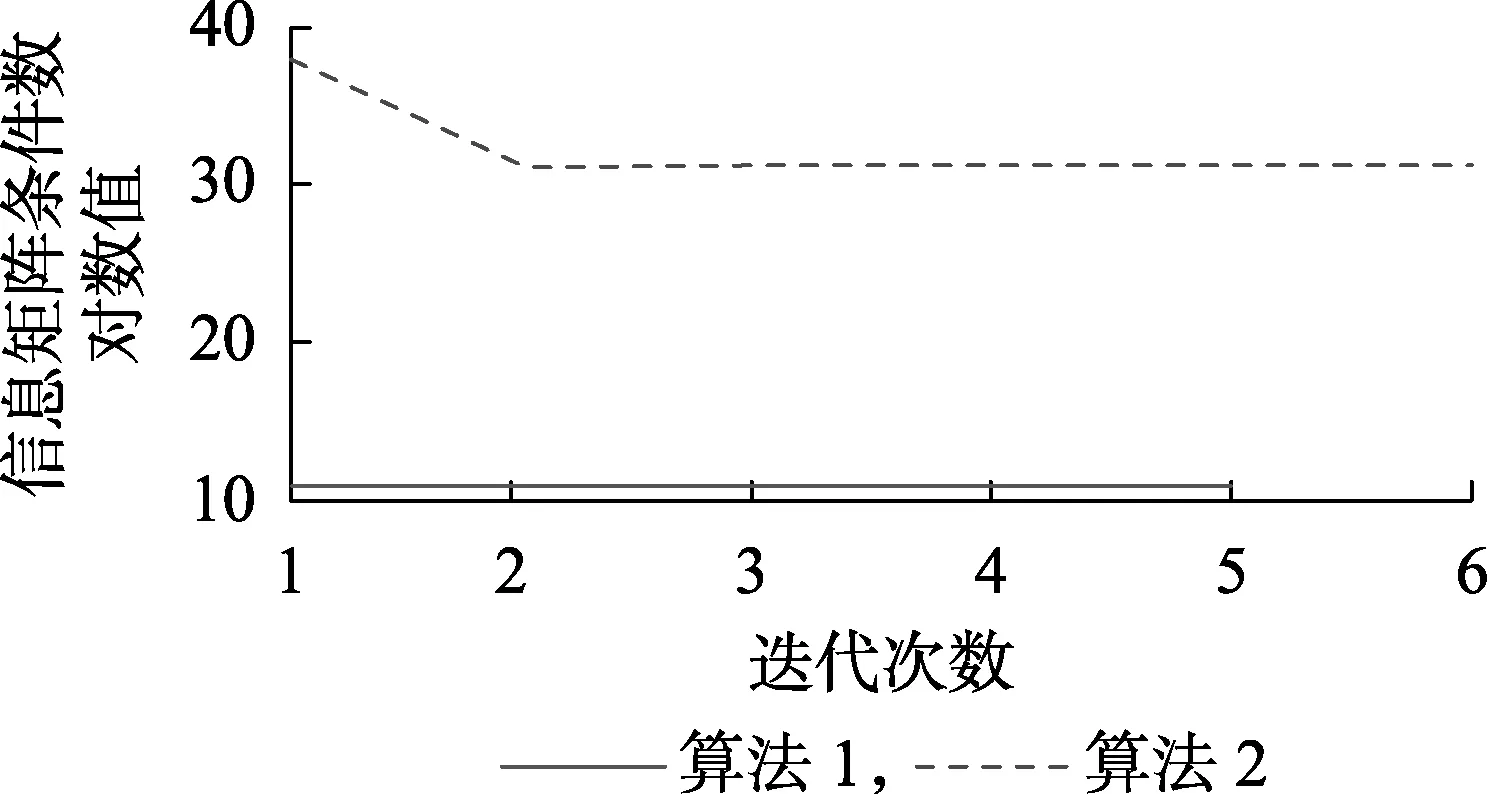
图3 信息矩阵条件数对数值随迭代变化曲线Fig.3 Logarithm of gain matrix condition number vs. iteration number

由图3可知，本文方法信息矩阵条件数远小于传统大权重法，数值稳定性问题得以改善。

5 结论

本文提出了基于DBN伪量测建模的配电网状态估计算法，并采用线性约束形式处理虚拟量测。DBN伪量测建模充分考虑了影响负荷的因素，利用与当前时刻负荷相关性较大的数据作为输入，与BP神经网络相比能够获取更精确的伪量测。另一方面通过等效电流量测变换分离虚拟量测并进行线性状态估计，严格保证了零注入节点功率为0，改善了数值稳定性问题，同时提高了计算速度，具备工程应用价值。

附录见本刊网络版(http:∥www.epae.cn)。