Quasinormal Modes of the Schwarzschild Black Hole Surrounded by the Quintessence Field in Rastall Gravity∗
2018-12-13JunLiang梁钧
Jun Liang(梁钧)
School of Arts and Sciences,Shannxi University of Science and Technology,Xi’an 710021,China
AbstractThe quasinormal modes of the Schwarzschild black hole surrounded by the quintessence in Rastall gravity are studied using the sixth-order Wentzel-Kramers-Brillouin approximative approach.The effect of the Rastall parameter on the quasinormal modes of gravitational,electromagnetic and massless scalar perturbations is explored.Compared to the case of Einstein gravity,it is found that,when η<0,the gravitational field,electromagnetic field as well as massless scalar field damp more rapidly and have larger real frequency of oscillation in Rastall gravity,while when η>0,the gravitational field,electromagnetic field as well as massless scalar field damp more slowly and have smaller real frequency of oscillation in Rastall gravity.It is also found that the gravitational field,electromagnetic field as well as massless scalar field damp more and more slowly and the real frequency of oscillation for the gravitational perturbation,electromagnetic perturbation as well as massless scalar perturbation becomes smaller and smaller as the Rastall parameter η increases.Compared among the quasinormal frequencies of gravitational,electromagnetic and massless scalar perturbations,I find that,for fixed η,(l,n),ϵ and Nq,the oscillation damps most slowly for the gravitational perturbation,mediate for the electromagnetic perturbation and most rapidly for the massless scalar perturbation,and the real frequency of oscillation is the smallest for the gravitational perturbation,mediate for the electromagnetic perturbation and the largest for the massless scalar perturbation in Rastall gravity.
Key words:quasinormal modes,Rastall gravity,Schwarzschild black hole surrounded by the quintessence field,WKB approximation
1 Introduction
In 1972,based on the idea that the energy-momentum tensor Tµνmay not be conserved in a curved spacetime,Rastall proposed a modification of the conservation law as[1]

where the semicolon denotes the covariant derivative,λ is a parameter,and R is the Ricci scalar.By requiring that Bianchi identities are still valid,he obtained modified gravitational equations

where Rµνis the Ricci tensor,gµνis the metric tensor and κ =8π (throughout this paper,we use the units G==c=1).The parameter λ measures the deviation from the equations of General Relativity.When λ=0,Rastall’s gravitational equations reduce to Einstein’s gravitational equations.Rastall’s theory reproduces in a phenomenological way,the absence of the Langrangian formulation leading to Rastall’s gravitational equations by implementing the variational principle in the context of the Riemaninann geometry is a major drawback of Rastall’s theory.[2−3]Nevertheless,equations similar to Rastall’s gravitational equations can be derivable from a variational principle in the context of Weyl geometry.[4−5]
Why consider the modification of the usual(classical)conservation of law for energy-momentum tensor?The arguments in favor of such a modification are summarized in the following points:
(i)The usual conservation of law for the energymomentum tensor was tested effectively only in the Minkowski spacetime.However,in a gravitational background,there will be inevitably an exchange of energy between matter and the gravitational field.Therefore,in principle,non-trivial generalizations of the conservation law for energy-momentum tensor are possible in a curved spacetime.[6]Rastall’s theory is one possible extension.
(ii)When quantum effects are taken into account in a curved spacetime,the propagation of quantum fields in the spacetime with horizons may lead to a violation of the usual conservation of law for energy-momentum tensor due to the chirality of the quantum modes.[7−8]This phenomena referred to as the gravitational anomaly.[9]
(iii)The non-conservation of the energy-momentum tensor is phenomenologically supported by the particle creation process in cosmology.At this point,Rastall’s theory may be considered as a classical formulation for the particle creation through its non-minimal coupling.[10]
(iv)The modification in the conservation of the energy-momentum tensor can lead to interest new per-spective to the analysis of gravitational systems,for example,the self-interacting scalar field formulation.[11]
(v)It was found that Rastall’s theory is agreement with various observational data in a cosmological context in recent years,[12−17]and thus Rastall gravity gained a renovated interest among researchers recently.
On the other hand,currently,the explanation for the present stage of the accelerating expansion of the Universe is a hot topic.One possibility is the quintessential dark energy model,[18−20]in which the so-called quintessence,a dynamical,spatially inhomogeneous component of the Universe,causes the acceleration.In 2003,a Schwarzschild black hole surrounded by the quintessence field in Einstein gravity was obtained by Kiselev.[21]Subsequently,some authors studied the quasinormal modes(QNMs)of that black hole for gravitational,electromagnetic and massless scalar perturbations by use of the thirdorder Wentzel-Kramers-Brillouin(WKB)approximative approach.[22−24](QNMs of black holes have been an attractive subject for a long time,for details see Ref.[25].)It was found that due to the presence of the quintessence,the gravitational(electromagnetic,massless scalar) field damps more rapidly.In this paper,we will extend the works to the case of Rastall theory,and use the sixthorder WKB approximative approach[26]to increase accuracy.The purpose is to explore the effect of Rastall parameter on QNMs.
The paper is organized as follows.In Sec.2,we briefly review the Schwarzschild black hole surrounded by the quintessence field in Rastall gravity.In Sec.3,we compute the QNM frequencies of the gravitational,electromagnetic and massless scalar field perturbations around the Schwarzschild black hole surrounded by the quintessence field in Rastall gravity,and then we further analyze and discuss the numerical results.Section 4 is a brief summary.
2 A Review of the Schwarzschild Black Hole Surrounded by the Quintessence Field in Rastall Gravity
The metric describing the Schwarzschild black hole surrounded by the quintessence field in Rastall gravity takes the following form[6]
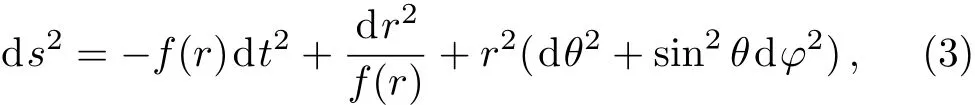
where the metric function is
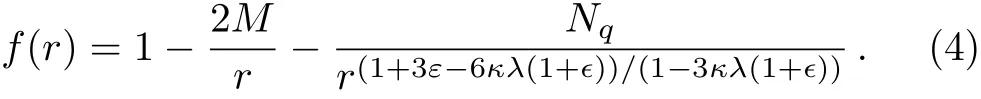
Here M is the mass of the black hole(we take M=1 henceforth for convenience),Nqis the quintessence field structure parameter and ϵ is the equation of state parameter of the quintessence field surrounding the black hole.When λ=0,we recover the Schwarzschild black hole surrounded by the quintessence field in Einstein gravity.[21]The energy density of the quintessence field can be written as

where
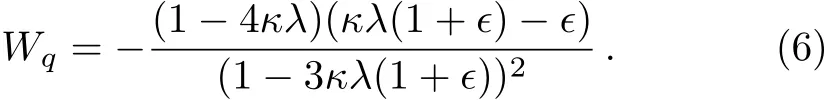
For convenience,we introduce a dimensionless parameter η = κλ.In what follows,we carry out some discussion on the range of the parameter η.
For quintessence field,the parameter ϵ has the range,−1< ϵ< −1/3.[21]We will focus on the case where ϵ= −0.7≈ −2/3[21]in this paper.In addition,in order to compare quantities and properties of the black hole in Rastall gravity and their counterparts in Einstein gravity,we choose Nq>0.[21]More specifically,we set Nq=0.01.Thus,the positivity of the energy density,i.e.,ρq>0,implies the condition Wq<0(see Eq.(5))which leads to the result−7/3< η<1/4(use Eq.(6)).In addition,considering that the parameter η should satisfy η>1/4 or η<1/6≈ 0.17 due to the entropy positivity condition[27]and that numerical calculation indicates that only>−0.49,there exists a cosmological horizon(the horizons of the metric(3)can be obtained from f(r)=0 by numerical method.)In general,there are two horizons,i.e.,the event horizon and the cosmological horizon for the Schwarzschild black hole surrounded by the quintessence field in Rastall(Einstein)gravity.From Fig.1,we see that,a smaller η leads to a larger cosmological horizon for the case in which Nq=0.01 and ϵ= −0.7,and if η≤−0.49,for instance,η=−0.5,there exists no cosmological horizon,thus we restrict the range on the parameter η as−0.49< η<0.17.

Fig.1 The metric function f vs.r,for various values of η.The long-dashed,solid,short-dashed and dot-dashed lines correspond to η =0.1,−0.05,−0.1,and −0.5,respectively.We have set Nq=0.01 and ϵ= −0.7.The corresponding one in Einstein gravity(η=0,Nq=0.01,and ϵ= −0.7)also plotted(thick solid line)for comparison.
3 QNMs around the Black Hole Surrounded by the Quintessence Field in Rastall Gravity
3.1 QNM Evaluation of the Gravitational Field Perturbation
For the gravitational perturbation,we deal with the Regge-Wheeler gauge.[28]In this gauge,the perturbation hµνare supposed to be very small compared with the background metric gµν,and the perturbation field equation is given by δRµν=0,where Rµνis the Ricci tensor.

where Pl(cosθ)is Legendre function with l being the angular quantum number,and ω is the complex QNM frequency.Wecan obtain from δR23=0,

and from δR13=0

Defining G=f(r)h1/r and dx/dr=1/f(r),where x is the tortoise coordinate,and eliminating h0in Eq.(9)by use of Eq.(8),we then obtain

where the effective potential Vg(r)is of the form
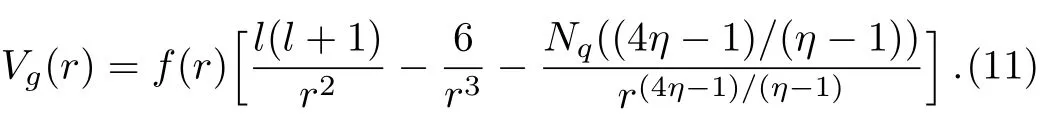
The boundary conditions defining QNMs can be written as

In Fig.2,we display the dependence of effective potential Vgon radial coordinate r for the gravitational perturbation around the black hole surrounded by the quintessence field in Rastall gravity.The corresponding effective potential in Einstein gravity is also plotted for comparison.
Figure 2 shows that,when η<0,the potential barrier becomes higher and wider compared with the corresponding one in Einstein gravity,while when η>0,the potential barrier becomes lower and narrower compared with the corresponding one in Einstein gravity.The height and width of the potential barrier decrease as the Rastall parameter η increases.Therefore,one can foresee that the value of the Rastall parameter will have an affect on the QNM frequency.

Fig.2 The effective potential Vgvs.r for the gravitational perturbation around the black hole surrounded by the quintessence field in Rastall gravity with l=5,ϵ=−0.7,and Nq=0.01.The dotted,dashed,solid,dotdashed lines correspond to η = −0.4,−0.1,0.08,and 0.15,respectively.The corresponding one in Einstein gravity(η=0)is also plotted(thick solid line)for comparison.
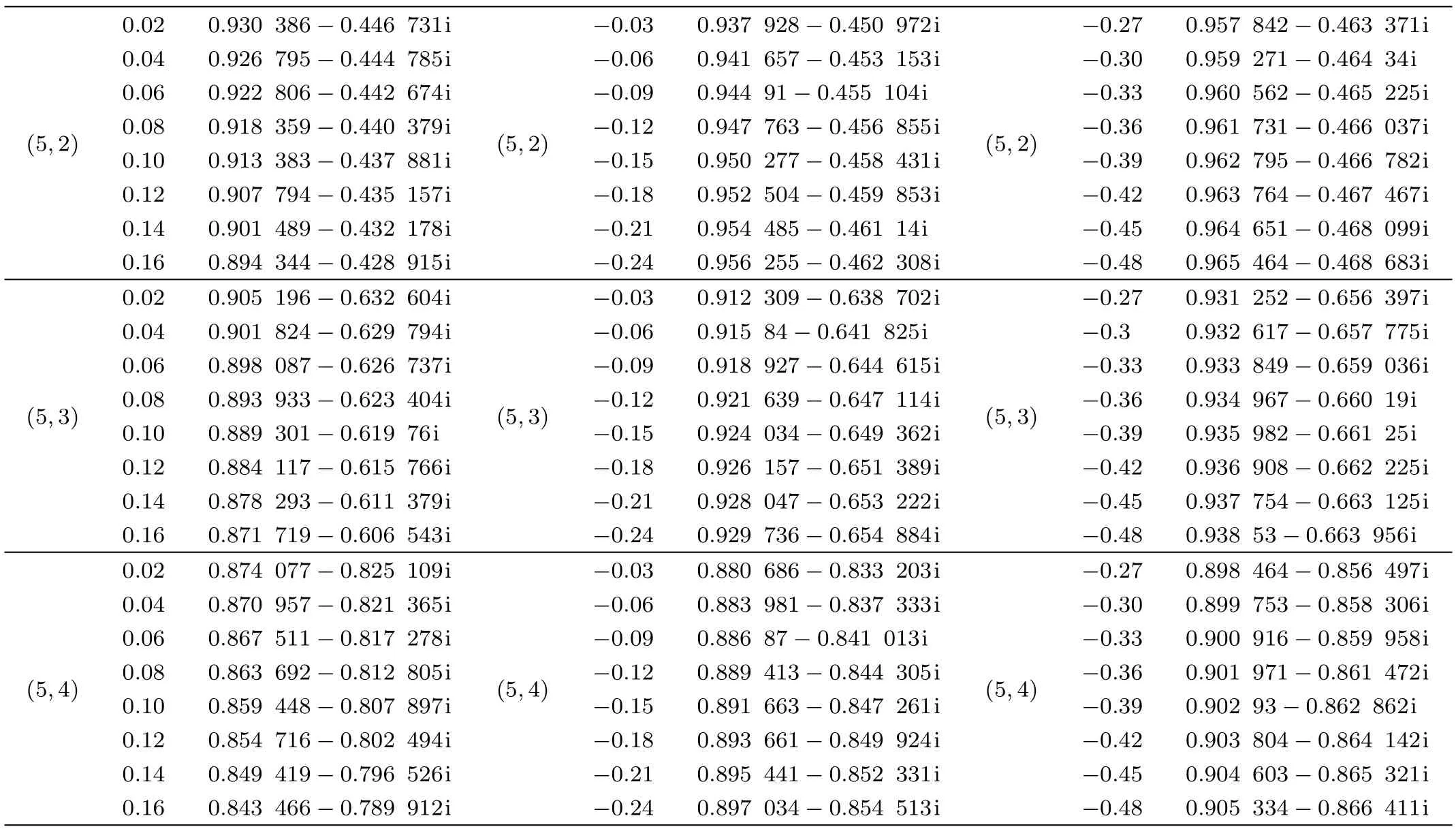
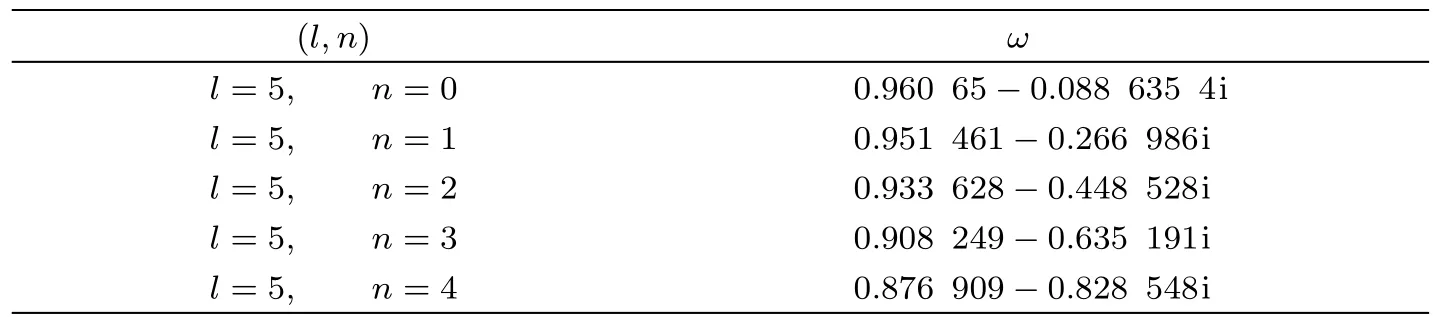
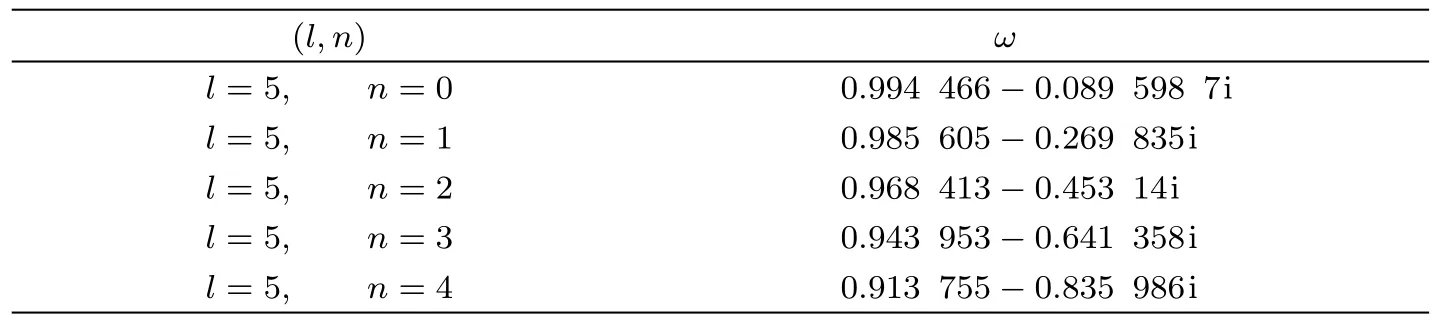
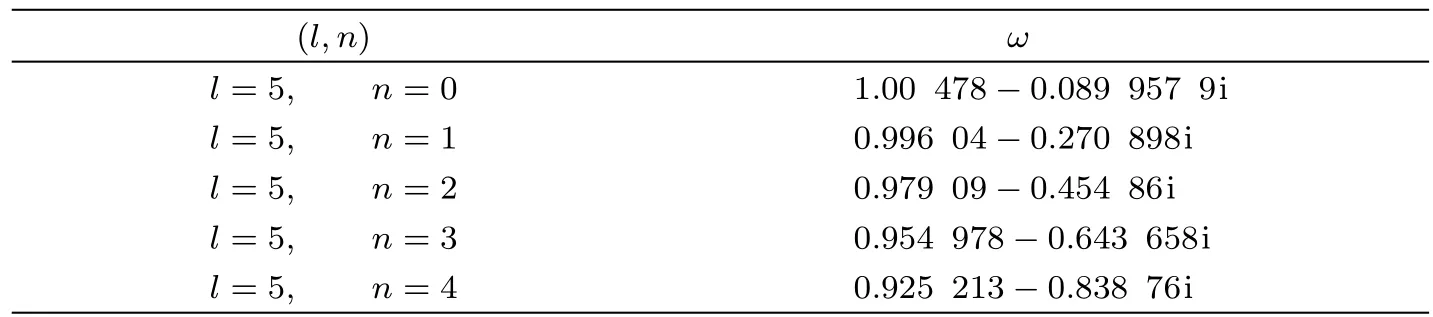
The numerical results of the gravitational perturbations using the sixth-order WKB approximation are listed in Table 1(the accuracy of the sixth-order WKB approximation is excellent for any n Table 1 Quasinormal frequencies of gravitational perturbations around the Schwarzschild black hole surrounded by the quintessence field in Rastall gravity for various values of the Rastall parameter η.We have taken ϵ= −0.7 and Nq=0.01. Table 1(continued) Table 2 Quasinormal frequencies of gravitational perturbations around the black hole surrounded by the quintessence field in Einstein gravity.We have taken ϵ= −0.7 and Nq=0.01. Using the electromagnetic field tensor Fµν=Aν,µ− Aµ,ν,with Aµbeing the vector potential,the Maxwell’s equations can be written as Expanding Aµin four-dimensional vector spherical harmonics[29] where Ylm(θ,φ)are spherical harmonics(see above),and m is the azimuthal quantum number.The first column has parity(−1)l+1,while the second(−1)l.Utilizing dx/dr=1/f(r),and substituting Eq.(14)into Eq.(13),we obtain[30] Here E(r)=ulm(r)is for parity(−1)l+1and is for parity(−1)l(the time dependence for E(r,t) ≡ulm(r,t)has been taken the form E(r,t)=E(r)e−iωt).The effective potential Ve(r)is of the form The dependence of effective potential Veon radial coordinate r for the electromagnetic perturbation is shown in Fig.3.The corresponding effective potential in Einstein gravity is also plotted for comparison.The numerical results of the electromagnetic perturbations using the sixthorder WKB approximation are listed in Table 3,which We have taken ϵ= −0.7 and Nq=0.01.For comparison,the corresponding results in Einstein gravity are also listed in Table 4,which we have taken ϵ= −0.7 and Nq=0.01. Fig.3 The effective potential Vevs.r for the electromagnetic perturbation around the black hole surrounded by the quintessence field in Rastall gravity with l=5,ϵ=−0.7,and Nq=0.01.The dotted,dashed,solid,dotdashed lines correspond to η = −0.4,−0.1,0.08,and 0.15,respectively.The corresponding one in Einstein gravity(η=0)also plotted(thick solid line)for comparison. Table 3 Quasinormal frequencies of electromagnetic perturbations around the Schwarzschild black hole surrounded by the quintessence field in Rastall gravity for various values of the Rastall parameter η. Table 3(Continued) Table 4 Quasinormal frequencies of electromagnetic perturbations around the black hole surrounded by a quintessence field in Einstein gravity. The massless scalar field is governed by the Klein-Gordon equation where−g is the absolute value of the determinant of the metric(3),and Ψ is the scalar field. Introducing Substituting Eqs.(18)and(3)into Eq.(17),we obtain the radial component of the Klein-Gordon equation in tortoise corordinate[26,31−32] where the effective potential Vs(r)is of the form In Fig.4,we show the dependence of effective potential Vson radial coordinate r for the massless scalar field in Rastall gravity.The corresponding effective potential in Einstein gravity is also plotted for comparison.The numerical results of the massless scalar perturbations are listed in Table 5,which we have taken ϵ= −0.7 and Nq=0.01.For comparison,the corresponding ones in Einstein gravity are also listed in Table 6,which we have taken ϵ= −0.7 and Nq=0.01. Fig.4 The effective potential Vsvs.r for the massless scalar perturbation around the black hole surrounded by the quintessence field in Rastall gravity with l=5,ϵ=−0.7,and Nq=0.01.The dotted,dashed,solid,dotdashed lines correspond to η = −0.4,−0.1,0.08,and 0.15,respectively.The corresponding one in Einstein gravity(η=0)is also plotted(thick solid line)for comparison. Table 5 Quasinormal frequencies of massless scalar perturbations around the Schwarzschild black hole surrounded by the quintessence field in Rastall gravity for various values of the Rastall parameter η. Table 5(Continued) Table 6 Quasinormal frequencies of massless scalar perturbations around the black hole surrounded by a quintessence field in Einstein gravity.We have taken ϵ= −0.7 and Nq=0.01. The real parts and the absolute values of the imaginary parts of the QNM frequencies as a function of η are plotted in Fig.5. Figure 5 explicitly shows that: (i)When η<0,the real part and the absolute value of the imaginary part of the QNM frequency for gravitational perturbation,electromagnetic perturbation as well as massless scalar perturbation in Rastall gravity are always larger compared with the corresponding ones in Einstein gravity.Thus,the gravitational field,electromagnetic field as well as massless scalar field damp more rapidly and have larger real frequency of oscillation in Rastall gravity.While when η>0,the real part and the absolute value of the imaginary part of the QNM frequency for gravitational perturbation,electromagnetic perturbation as well as massless scalar perturbation in Rastall gravity are always smaller compared with the corresponding ones in Einstein gravity.Therefore,the gravitational field,electromagnetic field as well as massless scalar field damp more slowly and have smaller real frequency of oscillation in Rastall gravity. Fig.5 Real parts and imaginary parts of QNM frequencies of the gravitational,electromagnetic and massless scalar perturbations around the Schwarzschild black hole surrounded by the quintessence field in Rastall gravity are plotted as a function of η.Filled up-triangles,down-triangles and circles denote values of the real(imaginary)parts of QNM frequencies of gravitational,electromagnetic and massless scalar perturbations in Rastall gravity,respectively,while empty up-triangles,down-triangles and circles denote values of the real(imaginary)parts of QNM frequencies of gravitational,electromagnetic and massless scalar perturbations in Einstein gravity,respectively.We have taken ϵ= −0.7 and Nq=0.01. (ii)For fixed(l,n),ϵ and Nq,the real part(absolute value of the imaginary part)of the QNM frequency is the largest for the massless scalar perturbation,mediate for the electromagnetic perturbation and the smallest for the gravitational perturbation.Therefore,the oscillation damps most slowly for the gravitational perturbation,mediate for the electromagnetic perturbation and most rapidly for the massless scalar perturbation,and the real frequency of oscillation is the smallest for the gravitational perturbation,mediate for the electromagnetic perturbation and the largest for the massless scalar perturbation in Rastall gravity. (iii)The real part and the absolute value of the imaginary part of the QNM frequency are always decrease as the Rastall parameter η increases.It means that the gravitational field,electromagnetic field as well as massless scalar field damp more and more slowly and the real frequency of oscillation for the gravitational field,electromagnetic if eld as well as massless scalar field become smaller and smaller as the Rastall parameter η increases.It is interesting to compare this result to those of other modified theory of General Relativity.Here,let us consider the QNMs of black holes in Einstein-aether theory(Einstein-aether theory is a local Lorentz-violating gravitational theory,in which a dynamical unit timelike vector field is introduced that defines a preferred time direction.Since this vector field never vanished and pervades the Universe,it is referred as to the “aether” field.[33]Einstein-aether theory gained much attention in the recent years.For a review on Einstein-aether theory see Ref.[34]). Konoplyna and Zhidenkc studied the QNMs of the non-reduced black holes for the gravitational,electromagnetic and massless scalar perturbations in Einstein-aether theory.[35−36]They found that the real part and the absolute value of the imaginary part of the QNM frequency increase with the aether coefficient c1for all three types of perturbations,which is completely different from the case of the Schwarzschild black hole surrounded by the quintessence field with the Rastall parameter η. In 2017,Ding studied the QNMs of two kinds of Einstein-aether black holes,which are termed the first and second kind aether black holes,[37−38]for the massless scalar and electromagnetic perturbations and found that,for the second kind aether black hole,both the real part and the absolute value of the imaginary part of the QNM frequency decrease with the aether coefficient c13,which is similar to the case of the scalar and electromagnetic QNMs of the Schwarzschild black hole surrounded by the quintessence field with the Rastall parameter η.In addition,Ding also found that,for the first kind of aether black hole,the real part of the QNM frequency for electromagnetic and massless scalar perturbations becomes smaller with c13increases.The absolute value of the imaginary part of the QNM frequency becomes bigger with small c13increases,and then decreases with big c13.Obviously,for the first kind aether black hole,the behavior of the real part of the QNM frequency is similar to that of the Schwarzschild black hole surrounded by the quintessence field with the Rastall parameter η.However,the behavior of the absolute value of the imaginary part of the QNM frequency is different from that of the Schwarzschild black hole surrounded by the quintessence field with the Rastall parameter η. Di ff erent from Refs.[22–24],in the context of Rastall gravity,we study the QNMs of gravitational,electromagnetic and massless field perturbations around the Schwarzschild black hole surrounded by the quintessence field.In addition,we use the sixth-order WKB approximative approach to increase accuracy.The aim is to explore the effect of the Rastall parameter on the QNMs.We only consider the case in which Nq= 0.01 and ϵ= −0.7≈ −2/3 in this paper,nevertheless,a similar study can be carried out for the case in which Nqand ϵ take other values and for the case of other field perturbations in Rastall gravity.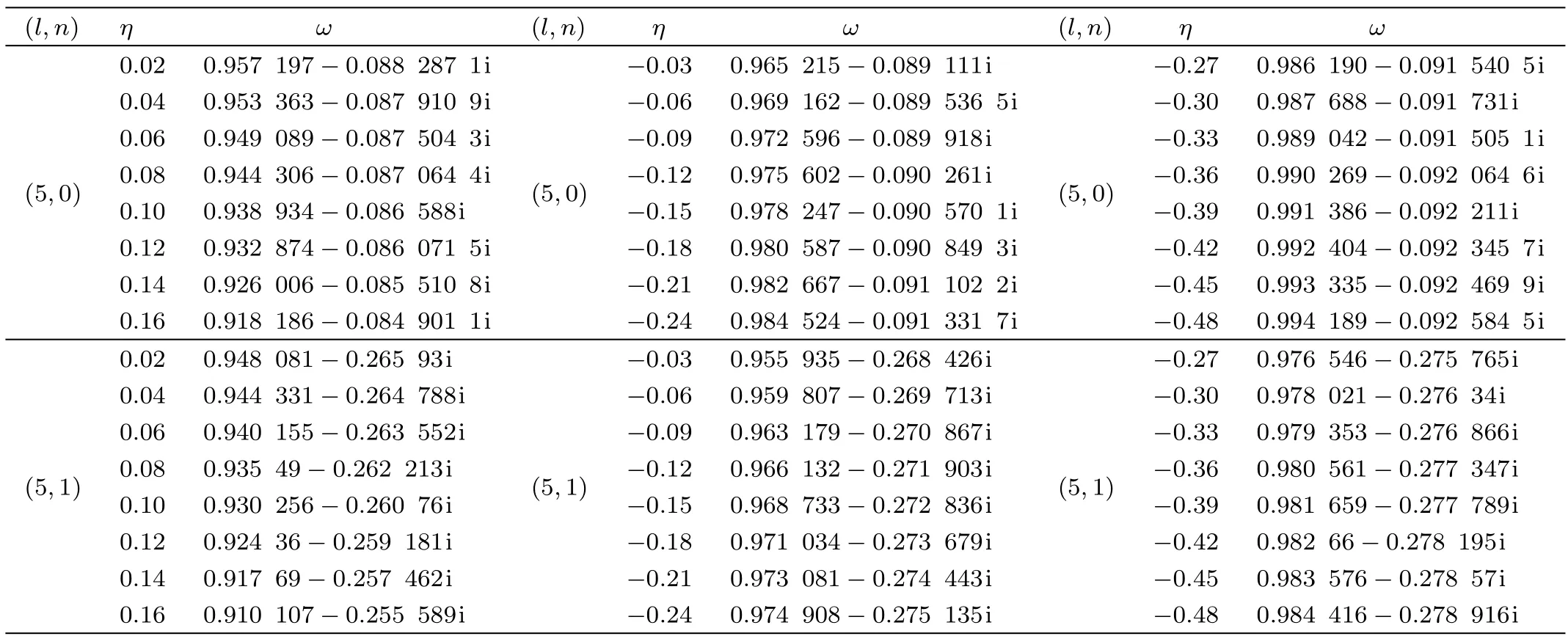
3.2 QNM Calculations of the Electromagnetic Perturbation

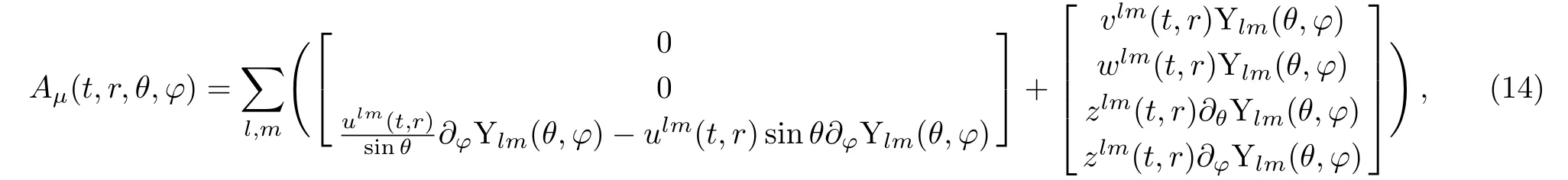






3.3 QNM Evaluation of the Massless Scalar Field Perturbation
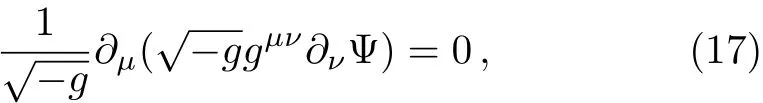






3.4 Analysis and Discussion

4 Summary
杂志排行
Communications in Theoretical Physics的其它文章
- Mixed Local-Nonlocal Vector Schrödinger Equations and Their Breather Solutions∗
- Circular Semi-Quantum Secret Sharing Using Single Particles∗
- Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation∗
- Runaway Directions in O’Raifeartaigh Models∗
- The 1/NcExpansion in Hadron Effective Field Theory∗
- Quasinormal Modes of the Planar Black Holes of a Particular Lovelock Theory∗
