通过函数变换探究函数零点的存在性

（山东省滨州市实验中学数学组 山东滨州 256600）

近两年，在全国高考试题和各地模拟试题中，有关函数零点的存在性问题是一个热门考点，理所当然的也就成为我们教学一线的热点问题。这类问题一般可以归结为已知函数f(x)在区间(a,b)上是单调函数，来探究函数在区间(a,b)内零点的存在性。在具体求解过程中，证明∃x0∈(a,b)，使得f(x0)＞0（或f(x0)＜0）成为一个探究性的问题，也是难点所在。究其原因主要有两个：一是函数f(x)一般由几个基本初等函数的和差积商或者复合而成，且构成f(x)的各个部分难以直接通过因式分解等手段联系起来，从而达到判断符号的目的；二是函数f(x)中含有参数，因为参数的变化导致探究x0的难度。下面以几个例子，阐述通过对构成f(x)的部分函数的变换，使构成f(x)的各个部分能有机结合起来，进而确定x0的方法和道理。

例1（2017·全国卷Ⅰ理·T21）

已知函数f(x)=a e2x+(a−2)ex−x。

（1）讨论f(x)的单调性；

（2）若f(x)有两个零点，求a的取值范围。

本例（1）的结论是：当a≤0时，f(x)在(−∞,+∞)单调递减。

当a＞0时，f(x)在(− ∞,−lna)单调递减，在(− l na,+ ∞)单调递增。

（2）（ⅰ）若a≤0，由（1）知，f(x)至多有一个零点。

（ⅱ）若a＞0，由（1）知，当x=− l na时，

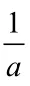
①当a=1时，由于f(− l na) = 0，故f(x)只有一个零点；

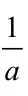
即f(− l na) ＞ 0，故f(x)没有零点；

因为− l na＞0，又通过观察f(x)的解析式的特征知，

x→ − ∞时，a e2x,(a−2)ex→0,−x→+ ∞，

所以必存在x0(− ∞ ,− l na)，使得f(x0)＞0。

又f( −2) =ae−4+ (a− 2 )e−2+2 ＞ −2 e−2+2 ＞ 0，

故f(x)在(− ∞,−lna)有一个零点。

这里是如何探究出f(−2)＞0的呢？

f(x)=a e2x+a ex−2ex−x＞ −2ex−x=−2(ex+x)，

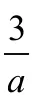
当x→+ ∞时，显然e2x在函数的变化过程中是主体地位，故可以考虑将−x缩小，

容易知道−x＞−ex，

所以f(x)=a e2x+(a−2)ex−x＞a e2x+(a−2)ex−ex

=ex[aex− ( 3−a) ]。

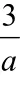
上面原函数的变形过程基于对构成原函数的基本初等函数及其变化规律的观察与分析。

则f(n0) = en0(aen0+a− 2) −n0＞ en0−n0＞ 2n0−n0＞0。

综上，a的取值范围为(0,1)。

例2（2016·全国卷Ⅰ文·T21）

已知函数f(x)=(x−2)ex+a(x−1)2。

（1）讨论f(x)的单调性；

（2）若f(x)有两个零点，求a的取值范围。

简析：因为f′(x)=(x−1)(ex+2a)，所以当a≥0时，f(x)在(− ∞ ,1 )上单调递减，在(1,+ ∞)上单调递增。

当a=0时，f(x)显然只有一个零点2；

当a＞0时，f(x)有极小值f(1 ) =−e＜0。

又观察f(x)易知f(2)=a＞0，

所以(1,2)内必存在唯一零点。

当x→ − ∞时，(x− 2 )ex→0，a(x− 1 )2→+ ∞。

如何探究？

探究一：

f(x)＞x−2+a(x−1)2＞2x−2+a(x−1)2=(x−1) [a x−(a−2)]。

探究二：

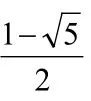
所以f(x)＞(x−2)ex−a(x−2)=(x−2)(ex−a)。

所以当x＜2且x＜l na时，必有f(x)＞0。

通过上面的例子我们不难发现，函数变换的过程是对f(x)放缩的过程，通过这种变换使得原来构成f(x)的难以沟通的各部分转化为基本初等函数，从而容易探究出x0，体现了转化与化归的思想。而如何完成这种函数变换，则需要实施者对函数f(x)的构成特点，参数的取值范围以及单调区间有一个细致的观察与分析，同时还需要掌握利用曲线的切线方程将复杂函数转化为基本初等函数。