考虑内外均衡安全增益的可量化社区隐藏算法

赵 霞 魏霖静 肖 君

1(甘肃农业大学信息科学技术学院 甘肃 兰州 730000)2(甘肃省计算中心系统集成部 甘肃 兰州 730000)

0 引 言

网络遍布于我们的日常生活中，网络的研究涉及到许多学科，从物理学到计算机、社会科学等诸多方面。网络分析中的一个重要任务是社区检测识别，即网络的区域(顶点子集)划分，以帮助其了解网络本身的结构和特征。

虽然社区检测研究非常广泛的课题，但很少有技术能够允许从社区检测算法中隐藏目标社区。本文研究的目的是提供这个问题的深入解决策略，称之为社区隐藏。可以从两个不同的层面对这个问题进行研究。隐藏技术对于想在Facebook或Twitter等社交网络中隐藏(作为群体)的用户是有用的。有观点认为，想要隐藏的社区不应该是网络的一部分，而从隐私权的角度，很多网络中的个体节点希望不被网络检测工具检测到。研究社区隐藏的另一个意义是：针对恶意目的的社区检测攻击，可以研究其作用机理，制定出有效的防御机制。在研究社区隐藏过程中，存在下列需要解决的问题：(1) 隐藏模型问题。这里通过关注成员节点所拥有的真实的网络知识量将社区隐藏问题处理为优化问题。然后，引入社区安全性指标，以隐藏函数作为优化目标。研究表明，基于最优模块化的社区隐藏策略需要对社区结构具有先验知识，这取决于产生这些社区的社区检测算法[2]。基于安全性的社区隐藏不会受到这个问题的影响。(2) 如何量化特定目标社区的检测算法的欺骗水平。通过引入隐藏指标，给出这方面的形式定义。(3) 高效算法的设计。社区安全性指标的高值优化，某种方法可以搜索所有可能的候选，但可能计算效率不符合要求。

本文研究的目的是展示在各种真实网络上，通过不需要全局网络知识的近似优化技术，可以找到好的隐藏解决方案。该算法可扩展到具有数百万个节点和边缘的网络，并且比社区检测算法快得多，能够先于社区检测网络算法完成社区的隐藏操作[3]。

1 社区检测隐藏问题描述

本节将描述社区隐藏问题，并提供一个问题示例。首先从一些初步的定义开始。网络G=(V,E)是一个无向图模型，其中V是网络模型的节点集，E是网络模型的边集。

(1)

类似地，可定义精度指标为:

(2)

(3)

2 考虑安全增益的可量化社区隐藏

2.1 社区隐藏问题模型

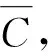
定义2(社区隐藏)令网络模型为G=(V,E)，给定目标社区C∈V，以及更新的预算β，则解决社区隐藏问题等于求解以下优化问题：

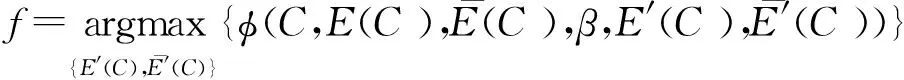
(4)

式中：函数φ(·)模型是一种社区隐藏算法；预算β限制了边缘更新的数量。隐藏函数φ与隐藏得分H的关键区别在于前者选择最大化φ的β变化，而H可量化目标社区C的理想属性(尽可能隐藏在检测算法的输出中)[6]。

2.2 社区检测隐藏算法框架

图1 社区隐藏过程

2.3 算法描述

本文的社区隐藏算法见算法1。算法1只考虑了C内边缘添加，而不考虑C间边缘删除。并且，为选择最优更新，仅需获得C内边缘/节点度即可[8]。因此，算法所需的网络知识量是有限的。

算法1基于安全性的社区隐藏

1. procedure COMDECEPTSAFENESS(G=(V,E),C,β)

3.np=getNodeMinimumAddRatio(C)；

4.nt=findExteralNode(np,C,G)；

6. (nk,nl)←getBestDelExclBridges(C)；

9. G←(V,E∪{(np,nt)})；

11.G←(V,E{(nk,nl)})；

12.β=β-1；

13. endwhile

算法1中，第3行getNodeMinimumAddRatio()可对于每个n∈C，计算在C以外的n个边缘的分数。第4行的findExteralNode()目的是找到边缘(np,nt)不存在节点的。第6行getBestDelExclBridges()分两个阶段执行；获得最佳的边缘链接；选择最方便的边缘更新，并将其应用于网络。最佳的节点添加和边缘删除策略，主要是基于式(4)所示的优化目标函数进行执行，具体可通过以下实例进行描述，如图2所示。

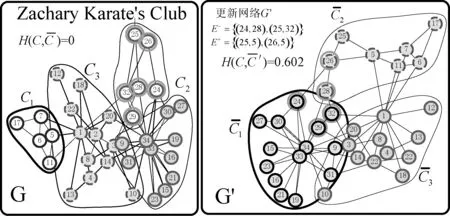
(a) 空手道俱乐部网络 (b) 更新网络模型图2 算法应用实例

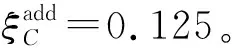
表1 网络更新计算过程

对于给定社区C和参数β，算法1对初始网络G进行更新，得到更新后的网络G′，满足σ(C′)≥σ(C)。对于算法1所示的基于安全性的社区隐藏算法，最佳的节点添加和边缘删除策略，可通过检测C中的所有节点添加和边缘删除计算获得[10]，其计算复杂度为O(|C|+|E(C)|)。节点添加和边缘删除过程的计算复杂度为O(|E(C)|)[11]。

3 社区检测隐藏算法的安全性分析

3.1 安全性定义

定义3(节点安全性)给定网络模型为G=(V,E)，社区结构C⊆V，以及社区C成员u∈C。则G中u的安全性σ(u,C)可定义为：

(5)

式(5)右侧次项中，给出u的边缘的一部分，并给出了u如何在网络内隐藏其度的解释。为了提高安全性，u应该多样化其连接，即与不在C中的节点有较高比例的连接。同时，在区间[0，1]中对式(5)和返回节点安全性值的两个分量进行加权。

从C成员的安全性角度，允许识别最不安全的成员并重新连接其链接以增加整个C的安全性得分。安全性控制社区的不同属性有可达性和内部/外部边缘平衡。

3.2 边缘更新对安全性的影响

1) 边缘添加：令网络模型为G=(V,E)，给定目标社区C∈V，C的安全性为σ(C)。令ξC=σ(C′)-σ(C)为安全增益。

证明：检测如果满足ξC=σ(C′)-σ(C)≥0，则有：

(6)

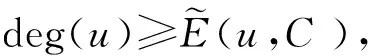
2) 边缘删除：本节主要从C内边缘进行边缘删除操作。

定理2C间边缘(u,w)删除，其中u∈C，w∉C，则对于给定的G′=(V,E{(u,w)})，ξC≤0始终成立。

证明：检测如果满足ξC=σ(C′)-σ(C)≥0，则有：

(7)

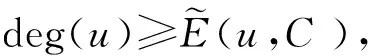
定理3社区C内边缘(u,w)删除，并不总是带来安全增益。

证明：假设删除边缘(u,w)之后，节点u和节点w在C中仍然保持的相同连通分量。需要满足下列条件：

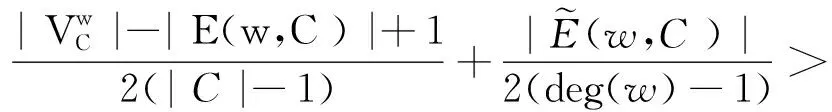
4 实验分析

4.1 实验设置

实验硬件设置：CPU i7-6400K 3.0 GHz，内存大小为16 GB RAM，操作系统为Microsoft Windows 7 旗舰版[13]。考虑了基线算法，随机地选择更新的类型和边缘添加/删除的端点[14]。为了验证本文算法的有效性，这里选取4种社区检测算法，检验社区隐藏算法的效果：(1) Louvain社区检测算法(Louv)，一种社区检测的多级模块化优化算法，其计算复杂度为O(|V|log|V|)；(2) InfoMap社区检测算法(Info)，其返回一个社区结构，并为随机游走提供了最短的描述长度，其计算复杂度为O(|E|)；(3) Edge-Betweeness社区检测算法(Edge)，为一个层次分解过程，其中边缘删除过程按照评估分值的下降顺序执行；(4) SpinGlass社区检测算法(Spin)，通过最大化加权社区聚类来实现图划分，基于三角分析策略实现对社区检测度量，其计算复杂度为O(|E|log|V|)。为了提高实验结果的稳定性，以下实验数据，为相同情形下运行上述4种社区检测算法的结果均值。

因为没有标准的基准来测试隐藏算法性能，这里设计了算法2中的方法进行评价。因为本文评价的是社区隐藏算法对于社区的隐藏程度，即它返回正确社区的能力与我们的目标是正交的。假设在最坏的情况下进行实验(第3行)，即假设目标社区C被完全发现。对于具体的检测算法，通过查看社区分布可选择不同规模的目标社区。

算法2社区隐藏性分析

1. procedure EVALUATEDECEPTIONALGOG (β,AD,D)

5.σ(C)←getSafeness (C,G)；

7.G′←applyDeception (G,C,β,Dx)/*x∈{s,m,r,w}*/；

10.σ(C′)←getSafeness (C,G′)；

算法2第4-6行可计算社区检测算法的模块性、安全性和隐藏评估得分，第7行给出的是更新后的网络G′。算法第8行，在G′上运行算法1计算社区检测社区的模块性、安全性和隐藏评估得分。上述评估算法的目的是调查：(1) 社区隐藏算法如何从检测算法中隐藏社区C；(2) 如何设定参数β；(3) 社区隐藏算法对社区结构的影响；(4) 社区隐藏和检测算法的运行时间。

4.2 结果分析

本文选取的实验网络有Zachary Karate’s Club(kar)、Dolphins association(dol)、Madrid Train Bombing(mad)、Books about US politics (polb)4种实验网络。表2给出了所考虑的网络的概述和选取的4种检测算法发现的社区数量。

表2 真实网络情形

表2中，给出的4种检测算法发现的社区数量存在一定的差异，这与算法的检测性能相关。上述实验数据出现小数的原因是本文选取运行20次的结果均值计算结果。SpinGlass社区检测算法在mad网络上的社区发现数量未得出，主要原因是该算法不能处理一定规模以上的网络。针对表2所示实验网络，参数β的取值区间是1～5，图3给出实验所得的社区隐藏指标实验结果。

(a) kar网络实验结果

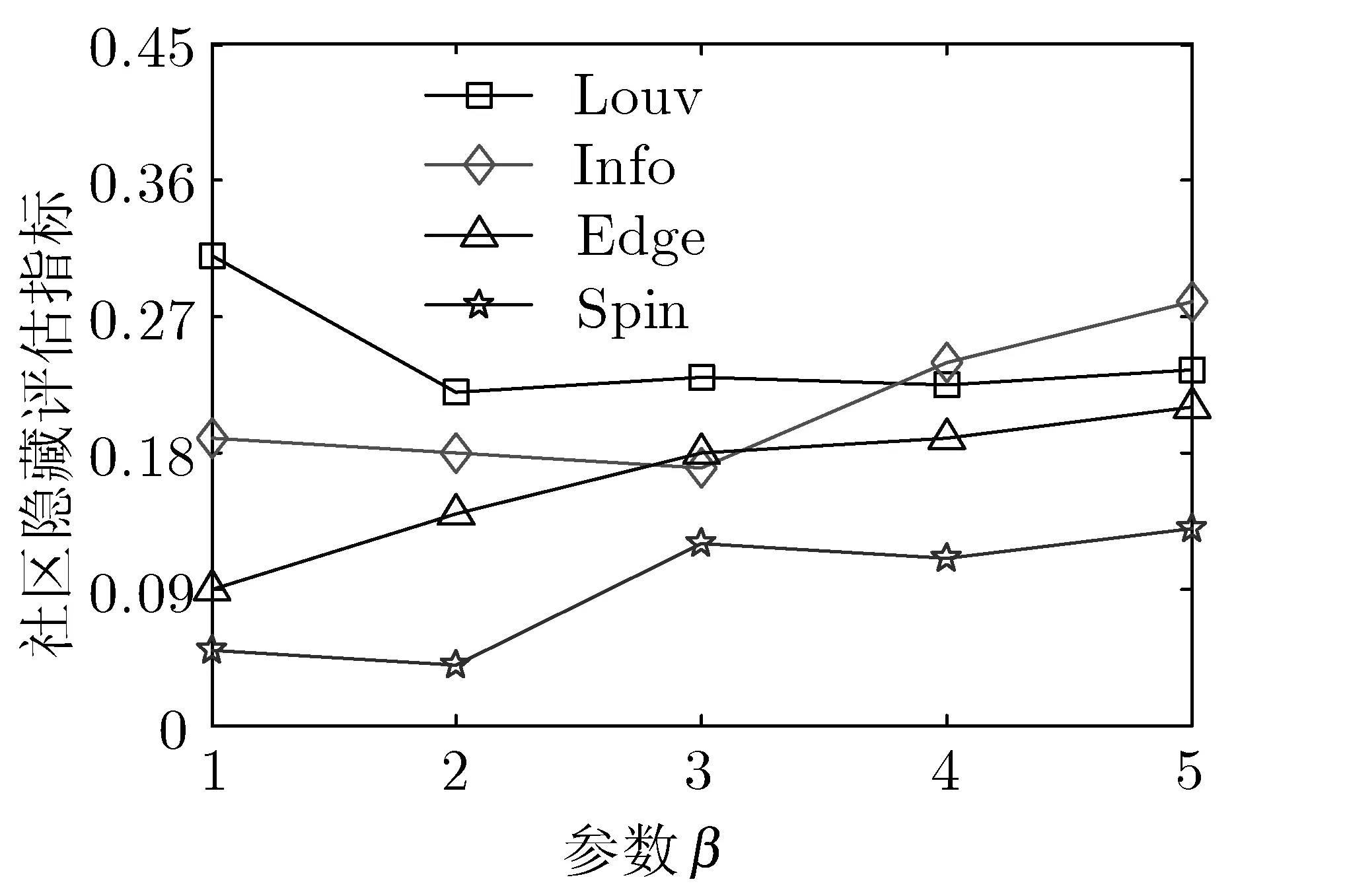
(b) dol网络实验结果

(c) polb网络实验结果

(d) mad网络实验结果图3 网络隐藏指标

根据图3所示网络隐藏指标实验结果可知，随着参数β的增大，几种算法在4种网络上的实验结果均呈现出增大的趋势。同时，可看出个别情形下呈现出波动性，对这样的行为可解释为：这些算法不是基于模块最大化的，算法产生一个更新网络，具有较低的模块化价值不会带来足够的中断INF的功能，产生更大的评估价值[15]。

此外，为更加直接地验证所提算法的社区隐藏性能，这里选取参数β取值为1～5，验证算法在kar、dol、mad、polb 4种实验网络上，更新前、更新后以及随机节点边缘调整方式的特定社区检测概率。该结果为每种算法运行30次的均值结果，见表3。

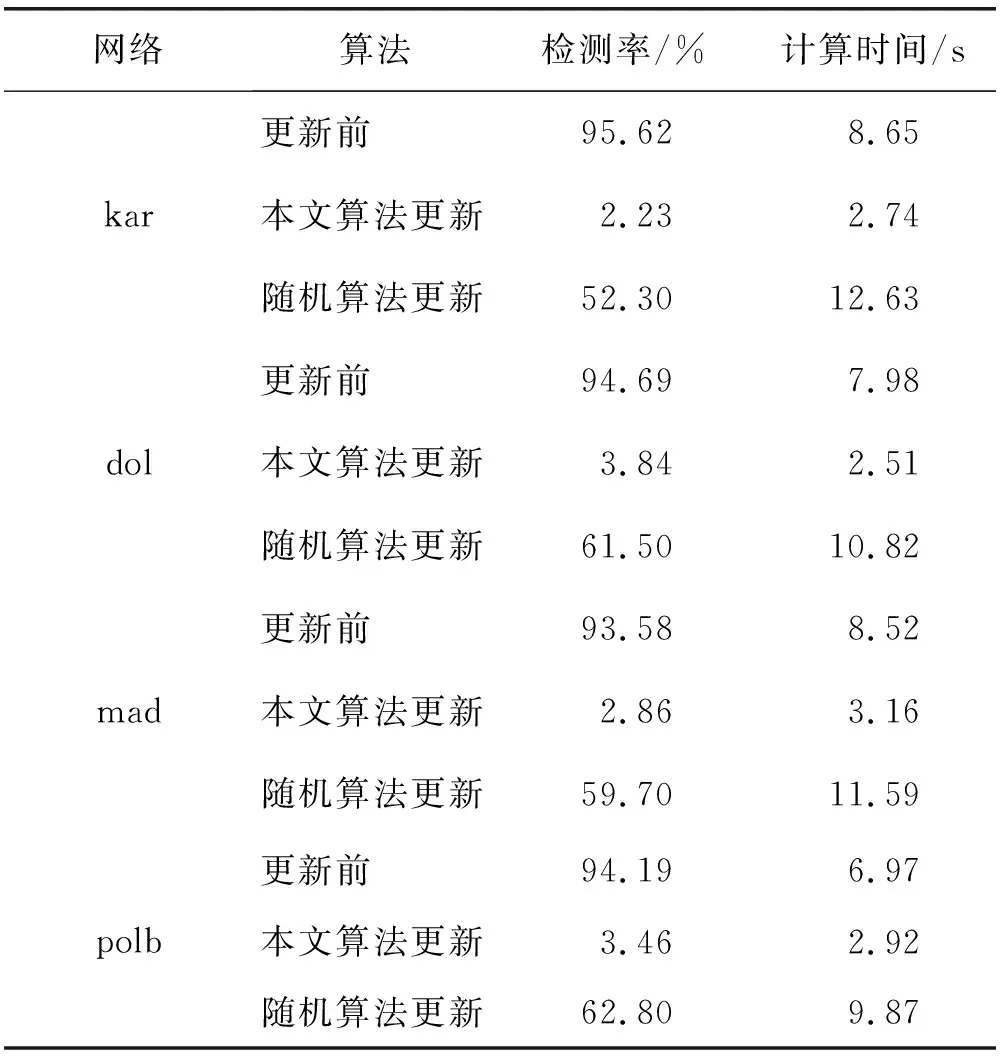
表3 特定社区的隐藏性能

表3所选取的特定社区选取标准是根据上述实验数据网络的真实社区划分结果选择的。其中本文方法和随机调整方式的节点和边缘更新数量均设定为5。根据表3实验结果可知，在特定隐藏社区的检测概率上，本文算法更新后的网络始终保持在较低的水平上，在3%左右。而更新前网络特定隐藏社区的隐藏性能相对较差，都达到了90%以上，随机更新策略的社区检测率也达到了50%以上，这体现出所提算法较高的社区隐藏能力。在算法的执行时间指标上，本文算法更新后的网络的运行时间2～4 s，而更新前网络的运行时间相对较长，这表明本文算法具有相对较高的社区隐藏效率，能够先于社区检测算法实现对社区的实时隐藏。

5 结 语

本文提出一种考虑内外均衡安全增益的可量化社区隐藏算法，在给出社区网络模型的基础上，对社区隐藏的评价指标进行定义，实现了社区隐藏的量化分析。然后基于社区检测的安全性增益指标对社区隐藏过程中的节点添加和边缘的删除策略进行研究。基于这些操作实现对网络社区的更新，最后对社区检测隐藏算法的安全性进行了理论分析，为社区隐藏算法应用提供理论基础。本文研究目的并不是如何获得更佳的社区隐藏性能，而是通过研究社区隐藏过程，探索其存在的共性因素，从而对社区检测算法起到更多的指导意义。下一步的研究重点是：探索自然网络中存在的有意或者无意的社区隐藏行为，分析其存在的物理意义，并有针对性的实现检测突破，这对于提升社区检测算法性能具有重要的意义。