基于全局-局部密度的准完全二分子图建模与挖掘方法
2018-12-13曹小钰
时 磊 刘 锐 虢 韬 杨 恒 王 伟 陈 玥 张 磊 曹小钰 罗 飞
1(贵州电网有限责任公司输电运行检修分公司 贵州 贵阳 550005)2(国网电力科学研究院武汉南瑞有限责任公司 湖北 武汉 430074)3(电网雷击风险预防湖北省重点实验室 湖北 武汉 430074)4(武汉大学计算机学院 湖北 武汉 430079)
0 引 言
在图理论中,两组对象之间的连接关系可以建模为二分图[1-2]。其中节点表示对象,边表示两组对象节点之间的关系。频繁连接的对象集合,往往是应用背景下有意义的社团群体。边的连接程度是找到这些有意义社团群体的重要特征。二分图中,全连接二分子图称为完全二分子图(biclique)。稠密的、近乎完全连接的二分子图称为准完全二分子图(quasi-biclique)。因为在数据分析中常常存在缺失、假阳性等问题[3],相对于完全二分子图,准完全二分子图不要求完全连接,使其具备容忍误差的优势,所以它更适合实际建模。
quasi-biclique可定义灵活的结构特征来满足不同应用。例如,Yan[4]提出α-quasi-biclique,要求一组中每个节点至少连接另一组中α%数量的节点。在α-quasi-biclique的基础上,进一步产生了δ-quasi-biclique[5],要求一组中的每个节点与另一组至少连接(1-δ)的节点。除了限制节点间连接数量,还有一类应用考虑准完全二分子图边的权重。例如Maulik[6]提出在加权二分图中找最大边值的准完全二分子图。
准完全二分子图的结构特征定义了在二分图中搜索的目标,搜索算法用于完成发现目标准完全二分子图。大多数准完全二分子图搜索是NP问题[5],但是相应工作均给出了近似优化解。Bu等[7]使用相邻矩阵来存储作用网络,并用邻接矩阵的谱去寻找特定的网络拓扑结构,其中具有负特征值的特征向量映射成准完全二分子图。Maulik等[6]提出了一种多目标遗传算法,同时优化了三个目标函数来获得目标准完全二分子图。Liu等[8]提出了一种基于Giraph用于发现最大顶点和最大平衡准完全二分子图的挖掘算法。文献[9]提出了一种具有灵活模块的BicNET算法,以发现具有参数化均匀性的类quasi-biclique模块。
现有的准完全二分子图结构定义和搜索方法依然存在不足。例如,α-quasi-biclique搜索时依然要求强条件:以完全二分子图作为核来扩展。δ-quasi-biclique虽然不需要以biclique作为核,但会低估所找到的quasi-biclique。另一方面,目前quasi-biclique 模型应用广泛,例如生物医学[10]、商业市场行为分析[11]和社会学研究[12]等。但是现有大多数针对解决某一具体领域问题提出挖掘目标quasi-biclique的算法,缺乏推广性,很难应用到其他情况。
本文从三个方面定义一种通用化的,基于全局-局部密度的准完全二分子图,在满足预设的密度阀值前提下,要求目标quasi-biclique规模尽可能大、内部尽可能稠密和外部尽可能稀疏,同时给出相应的启发式算法完成目标准完全二分子图的搜索。
1 方 法
1.1 基于全局-局部密度的准完全二分子图
给定两个二分图G=
quasi-biclique与biclique最大的区别在于对边完全连接的误差容忍。因此,与其他quasi-biclique结构特征目标不同,本文关注quasi-biclique边连接的稠密程度特征,通过定义quasi-biclique的内部密度θ度量该特征。
(1)
当B是G中基于全局-局部密度的quasi-biclique时,其密度θ必须大于给定阀值,为了使quasi-biclique密度特征更显著,综合文献[13-14],还要求其满足三个目标:
1) 最大规模:不存在满足θ阈值的另一个quasi-bicliqueB′,使得B⊂B′;
2) 内部稠密:对于有相同规模的quasi-biclique,其密度尽可能大;
3) 外部稀疏:对于具有相同规模的quasi-biclique,与G-B图中节点的联系边尽量少。
为了在给定的G中搜索到基于全局-局部密度的quasi-biclique,定义以下与密度相关的参量引导启发式算法搜索目标。
σr和σc度量B中行r的行密度和列c的列密度:
(2)
(3)
类似的,τr和τc度量N1-B1中行r的行密度和N2-B2中列c的列密度:
(4)
(5)
φr和φc度量N1-B1中行r的行内部一致性和N2-B2中列c的列内部一致性:
(6)
(7)
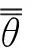
(8)
T1={r|r∈N1-B1,τr>0}T2={c|c∈N2-B2,τc>0}
1.2 挖掘方法
由于在二分图中搜索quasi-biclique已经被证明是NP问题,因此本文提出一种启发式算法来搜索基于全局-局部密度的目标quasi-biclique。算法流程如下所示。

Input: a matrix X of size N1*N2, a threshold ρ for mini-mal inner density, a threshold s for minimal row/colume in-cluded in quasi-biclique.Output: quasi-bicliquesFlag=Truewhile Flag doFlag=False, B=DeleteZeroDensity(X)D[ ]=DivideMatrix(B)for the ith matrix from 1 to length of D M1[i]=DetectKernel (ρ, s, D[i])endforif exist a matrix m1 in M1 whose density θ >ρ then find the matrix m1 whose |r||c| is maximal in M1 Q=ExpandKernel(ρ, s, m1,X) if Q is not null then output Q X=X-Q flag=True endifendifendwhileFunction DetectKernel (ρ, s, M){Calculate θ of M.while θ<ρ and |R| >s and |C|> s do Find the rows in M with the lowest σr Find the columns in M with the lowest σc if σr <σc then Remove the rows with σr from M endif if σr >σc then Remove the columns with σc from M endif if σr==σc and |R|≥|C| then Remove the rows with σr from M endif if σr ==σc and |R|<|C| then Remove the columns with σc from M endif Calculate the inner density θ of shrink matrix Mendwhilereturn M}

Function ExpandKernel (ρ, s, M, X){K=Mwhileθ>ρ and |R|>s and |C|>s do Keep the old record M=K Find rows outside K but in X with largest φr Find columns outside K but in X with largest φcif φr >φc then the rows with largest φr on K is added into Kendifif φr <φc then add the columns with largest φc into Kendifif φr==φc and |R|≥|C| then the columns with largest φr on K is added into Kendifif φr ==φc and |R|<|C| then the rows with largest φc on K is added into K endif Calculate the inner density θ of matrix K endwhile return M}
以上启发式搜索算法通过内部密度,行和列密度,以及内核引用的行和列内部一致性决定哪些行或列被删除(在内核搜索中)或添加(在内核扩展中)进行搜索目标。整个过程包括四个主要部分。
1) 去空行/列 DeleteZeroDensity去除密度为零的行和列。如果输入的矩阵是稀疏矩阵,DeleteZeroDensity可以降低数据处理的规模。
2) 对角化判断与分割 DivideMatrix检查待处理的二分图邻接矩阵是否存在对角化情形。如果存在,则分割,返回非对角化的所有子矩阵构成的数组。邻接矩阵存在对角化会影响内核发现和扩展。因此,要求内核的搜索是在非对角化的矩阵中进行。
图1展示了二分图G的邻接矩阵是对角化(反对角化类似)的例子。G是对角化,当且仅当存在G=A∪B。其中A=

图1 对角化举例
假设G的邻接矩阵D是如图1所示可以被分成两个小的非对角矩阵A和B。在搜索quasi-biclique的内核时,需要使内核的内部密度不断提升,直至满足预置的密度阀值。但是如果在对角化的不同子矩阵中寻找内核,这样会使密度减小,所以有如下定理1。
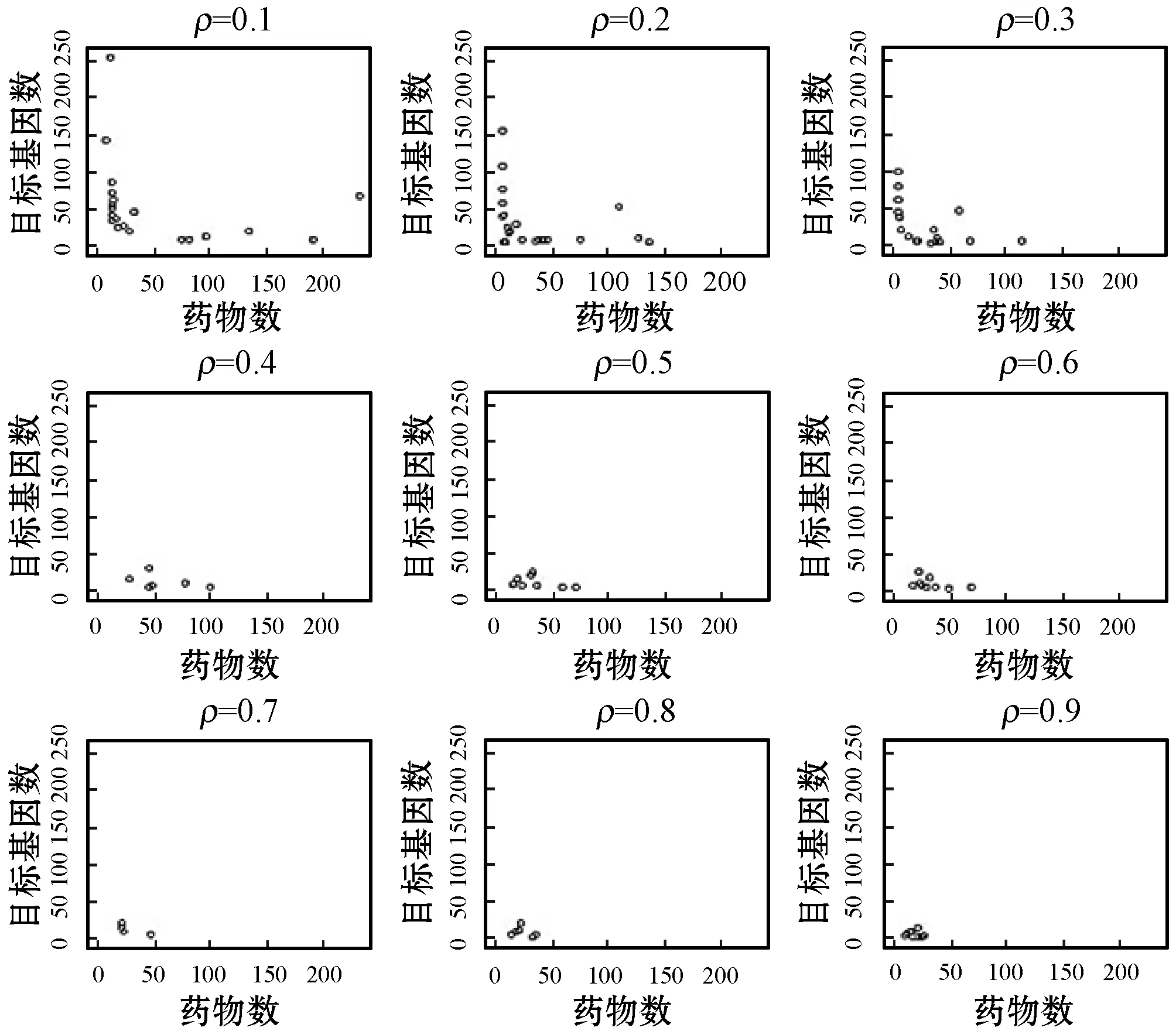
定理1将B中的任何行或列添加到A中,则新矩阵密度必有r2 证明:以添加一行为例。假设k1是矩阵A中的值为1的个数,那么按式(1)的计算方法,A的密度r1有: 设k2是新加入行中的1的个数,则加入行后的新矩阵密度r2为: 因为所有密度为零的行和列都已从D中删除,则有: k1≥|A1|,k1≥|A2| 为了证明r1恒大于r2,可以转换为证明r1-r2总大于零: 由于分母恒大于零,所以只需要考虑分子。展开分子后得到: Numerator=k1|A1||A2|+k1|A1|k2+k1|A2|+ k1k2-|A1||A2|k1-|A1||A2|k2= k1s2+k1k2+k2|A1|(k1-|A2|) 因为k1≥|A1|,即分子总是大于零,所以r2 以上证明说明了需要对原始输入矩阵进行对角化检查与分割。 3) 搜索quasi-biclique内核 DetectKernel负责确定quasi-biclique的内核。DetectKernel是在经过分割后的非对角化子矩阵上通过移除低密度部分找到满足密度要求的quasi-biclique无误差子结构。相比其他方法,本方法并不是搜索无误差的biclique结构,增加了方法适用的灵活性。具体搜索quasi-biclique内核时,是以行、列密度作为指标,移除低密度行或者列。当行列密度相等时,算法试图优先去除行列维数较大的一维。这样可以使得搜寻的quasi-biclique内核趋向于方阵。在有些具体的应用中,当期望行、列位置上代表的对象有均等的机会出现在最终quasi-biclique中时,适合采用此策略。当两组对象之间有重要度差异,相应地可以考虑优先保留重要一组对象。每当一轮去除低密度部分后,将计算当前状态下的内部密度值,当密度要求满足阀值时,搜索内核停止。 4) 扩展内核 以DetectKernel确定的内核为基础,ExpandKernel在原始输入的二分图邻接矩阵上确定最终目标quasi-biclique。由于DetectKernel确定内核过程中可能去除了一些有用的行或者列,所以内核扩展是增加在内核搜索时误删的行或列。在扩展过程中,需要考虑内核外部行列与内核的一致程度,从而决定哪些外部的行或者列可以加入到内核中。所以,此步骤操作中是以内核外行或者内核外列的内部一致性指标作为依据,选择扩展部分。扩展过程中,伴随着行、列的增加,quasi-biclique密度会随之下降,当不再满足阀值要求时,对该内核的扩展搜索停止。 本文使用R语言实现搜索基于全局-局部密度quasi-biclique的算法。算法在个人PC上实现,硬件平台CPU为Intel i5-4440,RAM为16 G。本算法的主要操作是比较矩阵的行、列之间的相似性与一致性,所以在R的程序实现中,通过apply函数代替所有循环操作,从而极大地提高了程序的求解速度。 如前所述,大部分quasi-biclique挖掘方法是整合在具体应用中的,没有独立的源程序,这样不能准确地复现或者直接应用到其他领域。为了客观比较性能,选择提供源码的PPIExtend[6]与本方法进行比较。比较实验使用的数据集是酵母蛋白质相互作用关系。它包括了4 959个蛋白质和它们之间10 640条作用边。当输入参数为(0.1, 5, 5)时,PPIExtend耗时约500秒搜索到了59 124个quasi-biclique。在(0.9, 2, 2)参数下,本方法耗时约70秒搜索到8个quasi-biclique。为区别两个方法的结果,PPIExtend搜索到的quasi-biclique记为LQB,本方法记为GLDQB。GLDQBs和LQBs分别含有109和155个蛋白质,其中71个蛋白质相同。 首先,比较分析PPIExtend方法和本文方法挖掘结果相互覆盖度。对于两个quasi-biclique:X1= 然后,考察本方法的条件约束效果。表1显示GLDQB关键指标项,依次为:内部密度、外部密度、背景(以LQB为参照,具有与对应GLDQB相同大小的LQB个数)和外部个数(背景中外部密度小于GLDQB的LQB个数)。 表1 GLDQBs主要指标 表1中所有的GLDQB的内部密度要远大于其外部密度。1、2、6、7和8号 GLDQB没有相应的背景LQB,说明本方法发现了与PPIExtend不同的quasi-biclique。“外部个数”的数目反映出本方法能恰好满足密度阀值的情况下使得quasi-biclique规模最大,而且“外部个数”占“背景”比重小,反映LQB的外部密度稀疏性不如GLDQB,从而体现出GLDQB出的全局-局部密度的内外部密度的显著性特点。 药物可以对多个基因起作用,一个目标基因可能受多种药物的影响[15-16]。本文不考虑多肽类药物,从DrugBank 数据库中收集已批准的针对人类疾病的1 186种小分子药物与1 141个目标基因,总计4 594种药物-基因相互作用。通过利用准完全二分子图可以帮助了解药物和目标基因之间的频繁关系,同时可推测未知的药物与目标基因作用关系。 准完全二分子图搜索算法中需要设定的主要参数是ρ,它指定最终quasi-biclique必须满足的最小密度要求。该参数的大小会影响搜索时间。为了研究不同的ρ与运行时间的关系,ρ按步长0.1,从0.1到0.9依次执行搜索。图2是不同ρ下的运行时间对比。通过编程优化,quasi-bicluque搜索算法的实际运行时间是可接受的。当ρ为0.1时,用时最长,需要37秒。同时,结果表明算法的运行时间并不是与ρ成完全反比。 图2 不同ρ取值下的运行时间 图3是上述实验在对应ρ下挖掘准完全二分子图个数。当ρ增加时,密度阀值增加,所以quasi-biclique的数量首先降低,相应地运行时间也会降低。当ρ超过0.7时,矩阵中的中等密度区域被分解成许多小密度的quasi-biclique。因此,quasi-biclique的数量又会增加,需要的时间也会相应增加。 图3 对应ρ取值下的准完全二分子图数 图4是以对应ρ值发现的每个quasi-biclique包含的药物和目标基因数。当ρ较小时,发现了代表药物数与目标基因数具有不平衡现象的quasi-biclique,即当ρ较小时,可发现一个药物针对多个目标基因,或者是一个基因可被多个药物作用的情形。随着ρ值的增加,发现的是代表药物与目标基因数趋向平衡的quasi-biclique,这与较小ρ的情形不同,表明ρ值与quasi-biclique的结点平衡特征也有关联性。 图4 不同ρ取值下,每个quasi-biclique包含的药物数 与目标基因数 生物意义上,取ρ=0.3的quasi-biclique分析生物功能特点。此参数下的quasi-biclique的基因包括许多典型的基因家族,如ATP结合盒(ABC)转运蛋白、酰基辅酶A脱氢酶家族、锌金属酶、钙电压门控通道亚基、G蛋白偶联受体等。quasi-biclique起到桥梁的作用,将某些目标基因家族与相应的药物治疗作用联系起来。例如,第16个quasi-biclique中包含了药物DB00143、DB01224、DB00404、DB00364、DB00211、DB01068、DB00245、DB05630、DB00521、DB00892、DB00517、DB01165、DB01104,药物功效包括了硫酸化蔗糖、治愈消化性溃疡、营养补充剂、抗高血压药、抗焦虑药、抗生素、消化药物、抗精神病药、抗惊厥药和抗焦虑药。针对基因有DRD4、KCNH2、RARA、RARB、RARG、RXRB、RXRG、HTR1B、HTR1E、HTR3A、HRH1、ADRA1A、ADRA1B。其相应的目标基因具有典型的精神病相关基因,如DRD4、HTR1B、ADRA1A。该quasi-biclique的内部密度为0.302,外部密度是0.031,内部密度相对外部的具有显著密集特性。该quasi-biclique中还有很多药物与目标基因之间没有报道有相关联系(即该连接元素为0),但是根据quasi-biclique中基因簇的功能相似,以及quasi-biclique内部0.3的密集联系的事实,该quasi-biclique内这些还未报道的药物与基因对之间客观上有很高的可能性是未知的药物与目标基因之前的作用关系,这可以为药物与基因研究提供提示。 本文考虑到局部特征(内部相关)和全局特征(外部稀疏),提出了基于局部密度(内部密度)和全局密度(外部密度)的quasi-biclique。它可以在大型二分图中捕获重要的子结构。通过分析和实验证明了基于全局-局部密度的准完全二分子图是发现双向关系合适的模型,其搜索算法也是有效的。介于基于全局-局部密度的准完全二分子图是一个通用的模型,它可以推广到社交网络、电力系统等许多其他领域。2 实验与讨论
2.1 对比实验

2.2 药物和目标基因数据应用


3 结 语
