港口集装箱装卸作业的Q-learning动态定价策略研究

余 珏 丁 一 林国龙

(上海海事大学物流研究中心 上海 201306)

0 引 言

国内港口的费率表主要是对不同箱型下各种尺寸的集装箱的装卸作业费用、中转费用等的描述。就港口装卸作业方面来看，港口企业在实际运作过程中会根据服务对象(集装箱)类型提出相应的收费标准(费率)，而这个收费标准相对来说是固定不变的。因此，国内港口均存在内外贸费率偏低且港口费率长期不变的问题，而国际港口的费率每年随市场变化进行调整。我国港口费率(即价格)长期不动导致双方差距逐渐增大，不利于港口经济发展。所以，我国港口也需要随市场变化调整费率，以缩减我国港口与国际港口间的差距，促进港口经济的发展。因市场变化由多种因素造成，包括有港口企业间的竞争关系，船公司的需求等。本文仅以船公司所提出的需求作为市场变化的衡量指标，从单船装卸作业时间的层面探讨研究在需求变化的前提下港口的定价决策问题。装卸利润是指港口企业的基本业务利润，约占港口企业总利润的80%以上，其变动的主要原因有装卸操作量、平均单位收入、单位成本等。定价策略的优劣会直接影响港口企业(为不同的船公司提供服务后)的装卸利润。在此前提下，本文将单船装卸作业时间作为需求，以单船装卸利润最大化为主要目标，研究港口在需求不断变动的环境下的定价策略，从而促进企业经济的发展，有效提高港口企业的竞争力。

根据研究意义可以看出，港口进行动态定价决策具有一定的实际意义。本文将研究有关港口企业的动态定价问题，分别对国内港口定价问题的相关研究和国内外动态定价的相关研究进行综述说明，从而得知动态定价问题的现有研究内容、方法和应用领域等。根据综述内容，本文将选择合适的方法并应用在国内港口企业中。

关于港口定价问题的研究：文献[1]使用运输成本优化模型估计潜在需求。文献[2]结合了两种工具来研究印度加尔各答危机港口系统，构建船舶行为微观经济模型;使用适当非线性方程的双重价格计算全均衡需求弹性(弹性)，将其与预期的利润最大化行为的基准值进行比较。文献[3]重点介绍了集装箱港口优化空间分配和最优定价的优先制度确定；考虑货物的内在、物流货物价值和集装箱各种要求的能力约束建立模型。模型在各个方向上扩展了经典价格差异理论，即反弹性规则。周鑫等[4]在改进的Hotelling模型基础上,构建双垄断港口企业的定价模型,以实例说明港口企业采用差别定价策略的动机。刘文忠[5]认为我国市场化导向的价格规制改革仍不完善，进一步改革的方向将集中在目前规制较为严格的外贸运输方面，应实行价格上、下限制。匡海波等[6]深入探讨低碳转型下的港口质押贷款利率决策理论,借助看跌期权反映客户违约风险、质押货物的碳排风险，采用VaR方法界定港口存货类质押率；建立低碳港口流动性较强存货类物流质押贷款利率决策模型。汪挺松等[7]针对目前船舶在港碳排放高的现象,提出引入价格补偿机制的港航合作模式：通过价格补偿机制对港方和船方在港航合作模式中的收益与损失进行分配。

关于国内外动态定价问题的研究：文献[8]采用了启发式算法研究标准的动态定价问题。文献[9]主要解决多目标动态定价问题。文献[10]使用时间归一化的收入或利润函数；以普通微分方程(ODE)方程的形式得出定价问题的分析解。文献[11]研究动态定价的线性、指数和多项Logitech模型，并且提出了使用神经网络模型以解决动态定价问题。文献[12]建立定价政策的问题来提高在固定期限内销售给定库存的收入；提出Q-learning和Q(λ)算法并比较使用蒙特卡罗模拟的学习算法的性能。文献[13]将具有随机扰动的库存系统被建模为连续时间随机微分方程；综合动态定价和生产控制，开发最大化总贴现利润的随机动态优化问题。文献[14]循一阶马尔科夫随机过程，参考效应导致最优价格路径与预期稳态价格的单调收敛，研究近期动态定价研究趋势，综述多产品、竞争以及需求信息有限的问题的文献。文献[15]主要研究一个垄断公司销售一种具有无限库存的单一类型产品的情况；在一定时间段内，产品的预期需求是随机市场过程和取决于销售价格的已知函数的总和。文献[16]提出价格应该随着时间的推移被打折，以最大化预期收益；使用动态递归，其中每个决策阶段根据经典经济垄断定价理论与销售数据估计的需求强度函数进行优化。文献[17]提出需求的不确定性是可以通过观察销售情况解决的；为卖家的最优动态决策问题制定了严格的上限，并使用马尔科夫决策过程(POMDP)框架来研究时尚产品卖家面临的动态定价问题。

基于以上综述分析得知：

(1) 这些港口企业对不同的船公司制定定价策略的文献均是从静态定价出发，很少考虑动态定价问题。文献一般以操作箱量作为需求进行研究，以装卸作业中单船装卸作业时间作为需求的文献不多。

(2) 目前有部分文献已使用相关理论方法确定库存或产品需求的动态变化带来的影响。本文就是在此基础上研究单船装卸作业时间变动的需求不确定性问题。现有文献中多数采用启发式算法求解供应链中的动态定价问题，采用Q-learning算法的研究并不多。

(3) 动态定价问题的主要研究对象为供应链中的定价政策问题，主要有库存问题、多产品竞争问题等，极少有关于港口动态定价问题的研究。解决动态定价的模型有线性、指数和多项Logitech模型，神经网络模型，连续时间随机微分方程，马尔科夫决策过程框架等。本文研究在市场环境不稳定的前提下港口企业的动态定价问题，马尔科夫决策过程适用于研究港口企业的动态定价问题。

因此，本文研究港口企业在应对不同的船公司提出的减少单船装卸作业时间的要求时，以单船装卸作业利润最大化为目标，采用Q-learning算法求解动态定价策略的问题。Q-learning算法改善了因单船装卸作业时间变动而导致单船装卸作业成本变动频繁的缺陷。

1 问题描述

港口吞吐量是衡量港口生产任务大小的主要数量指标，其中形成吞吐量的唯一来源是进出港口船舶所装卸的货物。装卸货物的时间即为单船装卸作业时间，该时间是制定动态定价策略的重要影响因素。某船只的装卸作业需要不同操作机械花费相应的时间进行装卸服务。装卸过程中调用不同的操作机械，且操作时间不同会产生相应的单船装卸成本，从而需要合理定价以达到单船装卸作业利润的最大化。

单船装卸作业时间的影响因素可以分为人为和技术影响因素。人为因素是指船公司所提出的减少单船装卸作业时间的要求；技术因素是指单船操作箱量，不同箱型和操作箱量需要不同的操作机械花费相应时间进行装卸作业服务。本文主要从人为因素出发，研究该因素下港口企业的动态定价问题，估计因人为因素导致的成本变动，确定单船装卸作业时间对定价的影响。本节通过船舶装卸作业的特点判断单船装卸作业时间的人为因素变动导致的成本变动原因：(1) 在船公司提出缩减单船装卸作业时间(即希望能够提前完成装卸任务)的要求时，港口企业需要调动各项操作资源，直接导致成本的变动。(2) 为提高对某船只的服务效率，需要变动船舶泊位计划，这势必会产生额外的成本费用，若定价不变则会导致利润减少，因此单船装卸作业时间对定价的影响十分重要。

本文不考虑船舶泊位计划变动产生的额外成本费用，以单船装卸作业时间为研究对象，由成本特性及单船装卸作业时间的重要性，确定动态定价过程如下：

(1) 对某到港船舶，确定单船操作箱量、单船装卸作业时间与不同箱型的操作箱量。

(2) 根据历史数据确定单船操作箱量与单箱价格、单船装卸作业时间的函数关系。

(3) 估计船公司提出的单船装卸作业时间变动要求所产生的预期估计误差，使用TDABC (time-driven activity-based costing) 方法[18]，从桥吊、内集卡、堆场机械资源时的角度来衡量额外的单船变动成本，得出单船总成本函数。

(4) 计算单船总成本并得出单船装卸利润，使利润最大化的定价即为最优单箱价格。

(5) 港口对同一船公司提供装卸服务，其单船装卸作业时间是不同的。船公司会在缩减单船装卸作业时间方面提出相同或不同的要求，本文将以箱型为分类变量得出更加精确的价格集。

本文中，港口对同一船公司的定价做出如下假设：在单船装卸作业时间给定的前提下，改变船公司对单船装卸作业时间的要求，即减少单船装卸作业时间，每一个要求会产生唯一的单箱价格集合。单箱价格与单船操作箱量和单船装卸作业时间具有一定关联性，为应对每个要求，选择合适的机械资源时策略，该策略能产生唯一的最小单船变动成本。

2 模型建立

因为港口对某船公司提供的装卸作业服务(即单船装卸作业时间)是不同的,相同的减少要求对不同的单船装卸作业时间的影响是不同的。所以模型中提出的所有参数均以固定的单船装卸作业时间为基础。

2.1 集 合

箱量类型集合I,I={1,2,…,n}，机械类型集合J，J={1,2,…,m}。

2.2 参 数

T(P,S):单箱价格为P、单船操作箱量为S和单船装卸作业时间T的函数关系式，由历史定价数据结合logit模型确定。

C:单船装卸总成本。

C1:单船装卸固定成本。

C2:船公司提出的减少单船装卸作业时间所产生的单船变动成本。

Tij:箱型i使用机械j进行操作时的单位作业耗用资源时(产能)，i∈I,j∈J。

cj:机械j的单位作业产能成本，即各操作机械类型：内集卡、吊桥、堆场作业时产生的单位作业成本，j∈I。

sj:机械j的操作箱量，即作业动因量，j∈J。

si:不同箱型i对应的箱量，i∈I。

Tcz:船公司提出需要减少的单船装卸作业时间。

m:单船变动成本可以增加的最大值。

2.3 决策变量

xij:表示是否选择改变箱型i所需机械j的资源时(产能)，i∈I,j∈J。

pi:港口对船公司提出的箱型i的单箱价格，根据港口对不同船公司的历史定价数据确定价格的上下限，pi∈[pl,ph],i∈I；pl、ph分别价格上、下限；0≤pl≤ph≤∞。

2.4 数学模型(DP)

(1)

约束条件：

pl≤pi≤ph∀i∈I

(2)

∀t∈N

(3)

∀t∈N

(4)

目标函数式(1)表示不同箱型的价格为p={p1,…,pi,…,pn}，与对应箱量为s={s1,…,si,…,sn}时的期望单船装卸利润最大化。单船装卸总成本C由单船固定成本C1和单船变动成本C2构成:

C=C1+C2

(5)

t∈N

(6)

式中：Ti(Pi,Si)是指得知历史单箱价格为Pi，箱量为Si时得到的单船装卸作业时间为Ti；T(P,S)是由历史数据集合：单船装卸作业时间集合DT(T1,…,Ti,…,Tn)， 单船的单箱价格集合DP(P1,…,Pi,…,Pn)和单船操作箱量集合DS(S1,…,Si,…,Sn)结合logit模型得出：

(7)

式中：b1、b2分别为历史单箱价格和历史单船箱量对于单船历史装卸作业时间的预期估计误差，B为客户基数。

因历史数据中未有明确的不同箱型的单箱价格，本文使用pt表示在t时刻所有箱型的平均单箱价格。将pt代入历史数据集合DP中寻找对应的P，并从集合DS得出相对应的S；将P和S代入式(7)求解得到t时刻对应的单船装卸作业时间T。

(8)

Ti(Pi,Si)为根据历史数据Pi、Si得出的单船装卸作业时间Ti，T(P,S)为由历史数据集合结合logit模型拟定的函数关系表达式。

3 基于Q-learning算法的港口动态定价策略

3.1 港口对于船公司制定的动态定价策略

Q-learning算法[12]是求解马尔科夫链(MDP)的值迭代方法，选择合适的动作状态对并在t时刻得出每一个状态state(s)采取某动作action(a)的反馈reward(r)；定义Q(s,a)表示每个状态s所对应a的效用值矩阵，更新Q矩阵：

Q(st,at)=Q(st,at)+α×(r+γ×

max(Q(st+1,a))-Q(st,at))

(9)

初始化：N、b1、b2、B、si、Tcz、单船操作箱量所确定的单船装卸作业时间T、探索率ε、折扣因子γ、学习速率α。

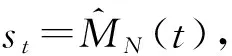
使用ε判定a是探索或学习，若a需要学习则利用目前Q矩阵中最大值Q所对应的a，否则在A中随机选择不同箱型的单箱价格作为a。状态值为s时采取动作a后得到下一个状态值，即s′。使用MATLAB调用yalmip工具箱计算0-1整数规划得到xij及其产生的单船变动成本C1，得到立即回报值r。

用式(9)迭代更新Q矩阵，在迭代终止时选择Q矩阵中的最优Q值得到s和a，即单船不同箱型的最优单箱价格。

最优Q矩阵中选定的a为港口企业在应对不同的船公司提出不同单船装卸作业时间的情况下，为达到装卸作业利润最大化的目标所制定的动态价格。

要注意的是，港口对同一船公司提供装卸服务，其单船装卸作业时间是不同的。最优单箱价格是指在固定单船装卸作业时间的前提下得到的不同箱型的价格集合。对某一单船装卸作业时间来说，改变Tcz得出的最优单箱价格集合是该单船装卸作业时间的动态定价表。港口对同一船公司的动态定价策略是由不同单船装卸作业时间的动态定价表构成的。

3.2 约束条件限制策略

算法1港口动态定价的Q-learning算法

初始化：

k=1,s=1,Q(s,a)=0，其中，s∈S,a∈A

设定ε、γ、α，大迭代次数κ

对于所有k≤K

Step1：状态s,使用ε-greedy策略选择利用或探索a

Step2：状态s下采取动作a，式(1)得到立即回报值r，式(8)得到下一状态s′

Step3：

Q(st,at)=Q(st,at)+α×(r+γ×max(Q(st+1,a))-Q(st,at))，s←s′

Step4：重复Step2、Step3；直到s′=max(s)时停止

约束限制策略如下：

1) 式(2)限定a∈A(s)，设定:

s={0,0.1,0.2,…,30}

2) 式(3)求解结果精确度在±0.01小时；式(4)最大成本值为5万元。

3) 已知s、s′、r；若r<0，令s′=s；否则由式(9)更新Q矩阵。

4)Q(s,a)矩阵维度大，规定s和a为单精度；为使得式(4)求解精确，计算s′时采用双精度，输出s′结果时调整为单精度。由精度引起的变动会导致一定程度上选取s所在id困难，规定若无法正确选取s的id，令s′=s。

4 案例分析

4.1 定价策略的细分及参数确定

为确保动态定价策略符合实际需求，以2016年上海港对船公司1的历史定价数据作为主要参考，并辅以其余3大船公司的历史定价信息，确定单船装卸作业时间和单船操作箱量的分界线。历史定价信息中并未有明确的不同箱型的单箱价格，仅以单船装卸总利润除以总箱量得出单船的单箱价格。式(2)的上下限如图1所示。结果表明：单船操作箱量分界点为2 000 TEU、单船装卸作业时间分界点为20小时；确定单船装卸作业时间的上、下限分别为10小时和40小时；上海港对船公司1、2、3、4制定的单箱价格下限分别为700元/TEU、300元/TEU、550元/TEU，510元/TEU，上限设置为1 000元/TEU。同时引入箱型因素，使得定价策略更为精确。基于上海港对船公司1的历史数据如表1所示。使用1stopt软件估计式(7)中的参数：b1=0.000 1，b2=0.728，B=1 653.4。使用2016年12个月的产能成本数据计算得出各操作机械的产能成本率，如表2所示。

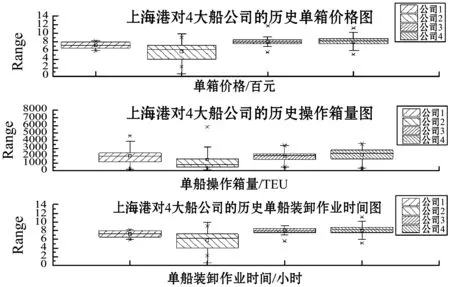
图1 上海港对4大船公司的历史单箱价格、单船操作箱量、 单船装卸作业时间的箱线图

单船装卸作业时间/小时单箱价格/元单船操作箱量/TEU11.5075625311.3366284212.678081 00411.007751 10811.507001 15810.506471 18011.838191 30311.257911 54623.338001 76711.005981 81922.508022 03922.336882 17723.507322 21022.337692 24224.166042 28423.006092 47125.005952 79923.507132 87733.678013 91134.506944 620

表2 各机械产能成本率产能

4.2 算法参数与单船装卸利润的分析

动态定价策略是根据不同的船公司对港口企业提出的减少单船装卸作业时间Tcz的要求制定的，不同的单船装卸作业时间在不同的Tcz变动影响下均能够产生相应的价格集。Tcz的变动会导致单船装卸成本变动，从而影响单船装卸利润，本节将使用单船装卸利润作为衡量指标。为了能够明确感受使用Q-learning算法制定的动态定价策略对于单船装卸利润的影响，本节从是否连续减少单船装卸作业时间进行举例说明。

首先，设定单船装卸作业时间Tcz均减少1小时，取滑动窗口N=21，根据4.1节中求解得出的参数，以上海港对四大船公司的历史单船装卸作业时间为主要依据，使用Q-leaning算法求解得出不同的最优单箱价格集合。因同一船公司在不同月份会有不同的单船装卸作业时间，即在1～12月份均由相对应的定价表，所得定价表的数据量过大，本文将12个月份划分成了四季。定价表将从单船装卸作业时间、单船操作箱量和季节三个方面综合得出上海港对四大船公司的定价表，如表3所示。相同月份中只要单船装卸作业时间不同，则会产生唯一最优价格。同时，不同月份中单船装卸作业时间相同或者不同时也有对应的唯一价格。因将12个月份划分成了四季，在表中显示的最优价格结合了季节中三个月的价格形成了最优价格区间。结果表明：上海港对不同公司在相同箱型下的定价策略受到单船装卸作业时间和单船操作箱量的影响。以公司1为例，当单船装卸作业时间小于20小时并变动至20小时以上的情况下，FR、RF的变动不明显，约在800～1 000元/TEU；GP、HC、OT和TK 在单船装卸作业时间小于或者大于20小时的情况下，随月份的增加价格趋势变动剧烈。从整体定价来看，除6月份外，定价随单船装卸作业时间的增长呈上升趋势，且在8到12月份间差距明显。单船装卸作业时间小于20小时的情况下，公司1-公司3的单船操作箱量均2 000 TEU以下；公司4则几乎没有单船装卸作业时间低于20小时的情况出现。上海港对不同的船公司定价时需要充分考虑船公司单船操作箱量和单船装卸作业时间，充分应对船公司提出的减少单船装卸作业时间的要求并制定合理以及详细的价格表。

表3 上海港对于4大船公司的定价表

其次，以上海港对船公司1的动态定价策略为例，本节从两方面举例说明动态定价策略如何应用于实际以及使用Q-leaning算法求解后其参数对于单船装卸利润的影响。(1) 船公司1要求减少的单船装卸作业时间不变，改变Q-learning算法中的参数。以折扣因子为例，随单船装卸作业时间的增长，折扣因子对单船装卸利润的影响如图2所示。结果表明：随单船装卸作业时间增长，单船装卸利润呈现单调上升趋势。折扣因子从0.1变动至0.7时，单船装卸利润增至352.77万元，0.7至0.9时降至159.89万元。(2) 船公司1要求减少的单船装卸作业时间发生变动，而Q-learning算法中的参数不变。以学习速率为例，船公司1要求单船装卸作业时间减少0.3、0.6、0.9、1.2和1.5小时，即={0.3,0.6,0.9,1.2,1.5}。学习速率对单船装卸利润的影响如图3所示。结果表明：根据单船装卸作业时间的减少情况，单船装卸利润随着学习速率的增加呈先增后减的趋势。例如单船装卸作业时间减少0.3小时的情况下，学习速率为0.3时单船装卸利润达到106.16万元；学习速率为0.9时单船装卸利润降至106.09万元。相同学习率，单船装卸作业时间由10.5小时减少至9小时的情况下，单船装卸利润波动明显。例如学习速率为0.7时，单船装卸作业时间为9.9小时，单船装卸利润达到最小值为105.90万元；单船装卸作业时间为9.6小时单船装卸利润达到最大值为106.14万元。因此，Tc2的变动和Q-learning算法中参数的变动对于单船装卸利润有显著的影响。

图2 以折扣因子为分类的装卸时间递增时的 单船利润趋势图

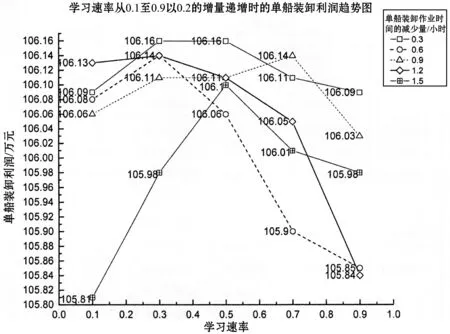
图3 单船装卸作业时间逐渐减少时的学习速率从0.1 至0.9以0.2的增量递增的单船利润趋势图

5 结 语

本文运用Q-learning算法求解得出港口企业对不同的船公司所制定的动态定价策略，得出以下结论：

(1) 学习速率越大，保留之前经验的效果越少；折扣因子γ越大，Q(s，a)作用越大。同时学习速率对于单船装卸利润的影响大于折扣因子，但是过大的学习速率、折扣因子会导致动作a被以往经验所限制，利润值陷入局部最优；过大的探索率会导致a过于自由探索，易忽略以往最优经验。在实际应用中，可以将今年的实际数据作为最终需要求解得到定价策略的依据，使用前几年的数据代入模型算法中求解得出合适的折扣因子和学习速率，并分析选择相应的折扣因子和学习速率作为已知条件，最后使用今年的实际数据得出相应决策。

(2) 上海港实际数据分析表明，对同一船公司在相同箱型下的定价策略亦受到单船装卸作业时间的影响。上海港对不同的船公司定价时，需要充分考虑该公司通常所需的单船操作箱量及单船装卸作业时间，制定合理以及详细的定价策略。本文所提出的基于Q-learning算法的动态定价策略可以有效提高港口企业的竞争力，能够及时有效地应对船公司提出的不同需求并得出相应的动态定价策略，促进港口经济的发展。从案例结果可以看出，单船装卸作业时间对单船装卸利润具有很大的影响。为提高单船装卸利润，港口可以从单船装卸作业时间着手，提高单船装卸效率，减少单船装卸成本。因单船装卸作业时间与港口装卸设备等一系列基础设施有关。为实现高效的单船装卸效率，港口可通过数字化、自动化技术，提升码头作业运作能力，改善港口信息不透明状况，提升对单船装卸作业流程的设备、人员等资源充分使用、检测、维修的能力。