基于多链MCMC方法的光伏出力序列预测研究

樊安洁， 高 山， 方济城 ， 韩海腾， 吴 晨

(1. 东南大学电气工程学院,江苏 南京 210096；2. 上海电力学院电子与信息工程学院， 上海 200090；3. 国网江苏省电力有限公司经济技术研究院，江苏 南京 210008)

0 引言

随着光伏发电渗透率的提高，光伏出力功率的随机性对电力系统的规划和运行提出了更高的要求。研究光伏出力时间序列的生成方法，更好地研究其出力的特性，对于进一步研究满足电力系统规划和运行具有重要的意义。电力系统的规划需要未来长时间的光伏预测出力数据作为分析基础，因此光伏出力功率预测模型应当能够从有限的实测数据中充分学习光伏出力的特性，保留历史出力的基本统计规律，涵盖影响光伏出力不确定性的各种因素。目前光伏序列的随机生成算法主要包括神经网络算法、支持向量机算法、卡尔曼滤波算法、马尔可夫链算法等[1-2]。其中传统一阶马尔科夫链模型在现有的风光发电功率的预测中取得了较好的效果，能够生成在概率特征及波动特性上与原始序列较为精确的预测序列[4-8]。

目前对光伏出力功率的研究主要集中在对单个光伏电源出力序列的模拟上。未来的电力系统规划中，为充分计及影响可再生能源出力不确定性的各项因素，在模拟可再生能源出力的时间序列时要考虑它们之间的相关特性[9-10]。文献[11]采用典型日方法描述无云状态下的太阳辐照情况，并引入向量自回归模型，较好模拟了历史出力中各分解成分的统计特征和各时间尺度下的波动特性，保留了光伏电站之间的相关性。但由于向量自回归模型的限制，该模型适合于短时期的光伏出力时序模拟，难以满足电力系统灵活性规划的要求。文献[12]采用交叉谱法对可再生能源和负荷之间的相关特性进行分析，提出了一种双链马尔模型对负荷和可再生能源出力序列进行预测。但该模型建立在已有精度较高的未来负荷序列的基础上，未能同时生成可再生能源和负荷的时间序列。

文中提出一种多链马尔科夫-蒙特卡洛(Markov Chain Monte Carlo，MCMC)方法，采用统一的离散状态定义将光伏出力序列转化为反映大气特征的离散状态序列，简化了仿真复杂度，建立了多条相互服从完全条件分布的马尔科夫链来模拟光伏电站上空的随机变化的大气状态，充分保留了光伏电站之间的相关特性。对3组不同相关程度的光伏电站仿真其出力序列，相较于传统单链方法，该方法在生成任意相关程度的光伏电站出力序列时均能较好地模拟光伏电站间的相关特性，其生成序列的基本统计参数和历史序列吻合度更高，验证了该方法在考虑相关性的多光伏电站出力时间序列预测中的有效性。

1 考虑相关性的多光伏电站出力组合预测方法

光伏发电受到地球公转和自转的影响，日地距离和太阳高度角呈现周期性变化，因此光伏出力也呈现出明显的规律性。和其他可再生能源相比，光伏出力主要呈现出季节特性与日特性、大气特性和随机波动特性这三大固有规律。在模拟光伏出力的固有规律的同时，考虑多个可再生能源对彼此出力不确定性的影响，基于MCMC法提出了考虑多光伏电站相关性的光伏出力序列的模拟方法。

1.1 数据处理

为了提高数据的准确性，需要对光伏电站的历史出力数据进行预处理，剔除错误的测量数据，补全空缺数据。对于连续日的数据空缺，采用线性插值法对空缺数据进行差值；对于内部个别数据空缺，采用非邻均值生成法进行填补。

1.2 多光伏电站相关性分析

利用相关系数分析多个光伏电站出力序列的相关程度，其计算方式为：

(1)

式中：X1，X2为任意2个电站出力序列；Cov(X1，X2)为序列X1与X2之间的协方差；Var(X1)为X1的方差；Var(X2)为X2方差。2个时间序列间的相关系数越大，其相关性越强。地理位置上越接近的光伏电站，太阳辐照情况相似度越大，则其光伏出力序列之间的相关性越强。相反，距离较远的光伏电站出力序列之间的相关性较弱。一般认为，2个时间序列间的相关系数大于0.7，则其具有强相关性。

1.3 建立考虑多光伏电站相关性的光伏出力预测模型

根据各个光伏电站出力序列的相关程度，建立多链马尔科夫模型，并对多个光伏电站的光伏出力序列进行预测，比较不同相关性程度下模型的预测效果。如果一个离散的时序过程在当前时刻的状态仅由上一时刻的状态所决定，该时序过程即是一个马尔科夫过程。无云状态下光伏出力序列的不确定性主要由大气状态所决定，而当前的大气状态和前一时刻的大气状态相关程度较高，因此可以采用马尔科夫链表征大气状态序列。

由于邻近地区光照情形类似，地区上空的大气层状况主要影响该区域内的光伏电站出力，因而光伏电站出力的不确定性受到周围区域光伏电站出力的影响。为了将光伏电站出力之间的相互影响因素考虑在内，在多个马尔科夫链之间引入相关性条件概率得到多链马尔科夫模型，将某变量下一时刻的状态看作该变量前一时刻的状态及其他变量当前时刻状态已知时的条件分布，对于多个光伏电站的出力进行模拟。

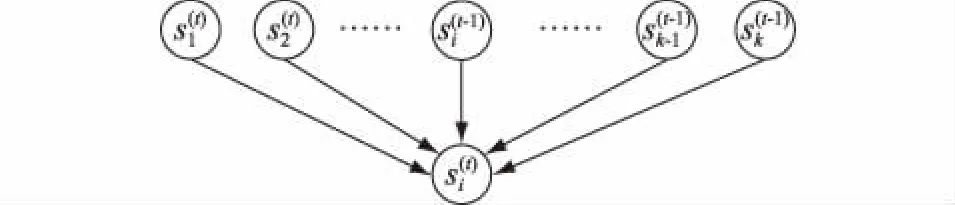
图1 多链马尔科夫过程Fig.1 Diagram of multi Markov Chain process

2 多链MCMC洛光伏出力预测模型

光伏出力预测模型包括离散状态划分、状态转移规律学习、蒙特卡洛状态抽样、光伏序列生成和修正四个部分。其具体流程如图2所示。

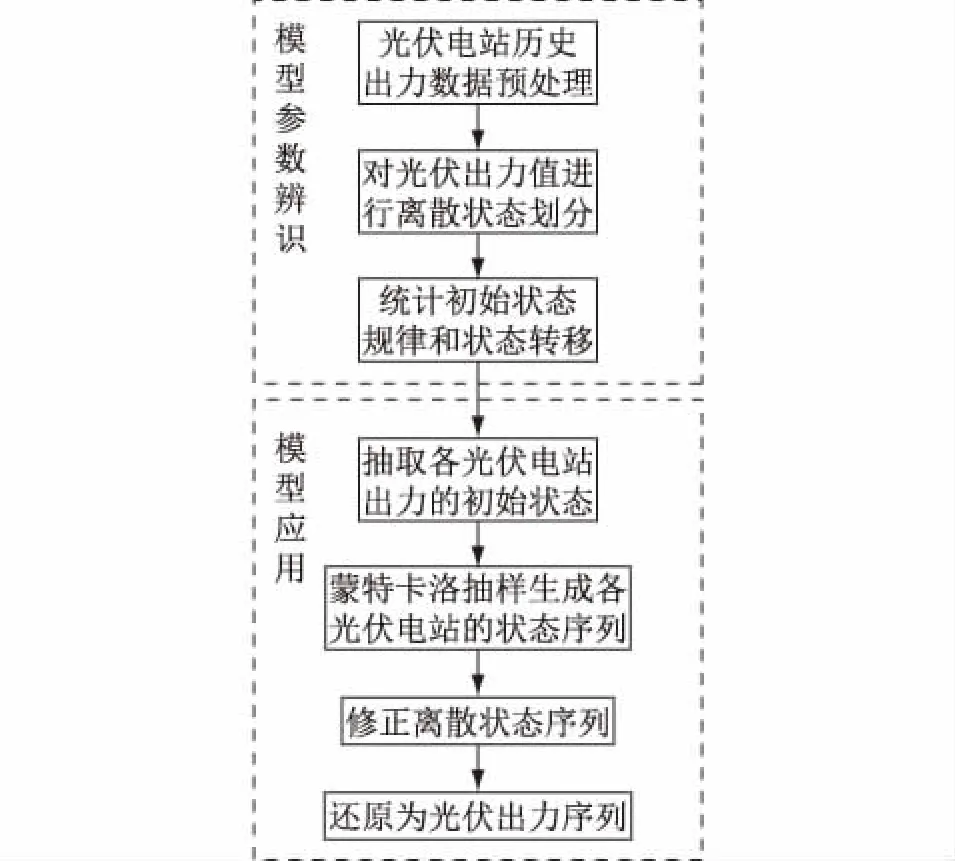
图2 多链MCMC方法组合预测模型流程Fig.2 Flow chart of PV power time series forecasting process using multi MCMC method

2.1 离散状态划分

马尔科夫链对应于一系列离散化的状态，因而对各个光伏电站的历史出力数据进行预处理后，将每一个发电功率值对应于特定的状态。文中采用一种统一离散状态定义的方法，避免传统马尔科夫模型对每个出力时段采用差异化的离散状态划分方法，降低了模型复杂度。离散状态的定义包含两个要素：出力范围和离散状态数。

离散状态的选取要能反应光伏出力的季节特性和日特性，假定一定时段内大气上空的太阳辐照度变化不大，可以将一年划分为M个时期，将一天内光伏的有效出力时间划分为T个时段，统计光伏电源在第m时期的每天第i个时段内的出力范围为(Pm,i,min,Pm,i,max)，将该出力范围划分为N个离散状态，每一状态覆盖的功率区间大小hm,i为：

(2)

该区间内某时刻的光伏出力P(t)对应的离散状态s(t)(s(t)∈{1,2,…,N})为：

s(t)=[P(t)/hm,i]

(3)

由于光伏电池板接收到的能够产生光伏出力的太阳辐照度主要受到大气状态的影响，因此N个不同的离散状态对应于N种大气状态。从而12个月份的光伏出力功率可以采用统一的离散状态定义，均转化为1,2,…,N表示的离散状态量，建立起一个历史状态序列。这种方法对于整个时间尺度上的历史数据建立统一的离散状态定义，进一步建立的状态转移矩阵无需区分季节和上下午时段，能够大大减少模拟的规模。

2.2 状态转移规律学习

2.2.1 初始状态规律

光伏出力的初始状态包括出力开始时间和起始离散状态。由于不同地区太阳辐照情况不同，为了使预测更加真实有效，模型在学习光伏出力历史数据规律的过程中，需要对各个光伏电站的出力开始时间和起始离散状态规律进行统计学习，便于后期抽样生成各光伏电站每日出力的初始状态。

2.2.2 状态转移过程

按照马尔科夫模型的参数学习的统计估算方法，根据大数定律，在样本数量足够的情况下以频率代替概率，计算各个状态之间的概率转移规律。

设某个区域内k个光伏电站的出力之间具有相关性，各光伏电站的离散出力状态用k维变量s表示，s=(s1,…,si,…,sk),si∈(1,…N)，第i个光伏电站在t+1时刻的出力服从以下分布。

(4)

由上式构成的状态转移矩阵Pi，其维数为Nk×N。以k=2,N=3为例，s1服从分布。

(5)

s1对应的状态转移矩阵P1可以表示为：

(6)

其中：

(7)

2.3 蒙特卡洛状态抽样

抽样生成服从完全条件分布的多条马尔科夫状态链的过程中，将状态转移矩阵作为抽样中的完全条件分布，依次对各个变量进行轮流抽样。抽样的具体过程如下：

(1) 设定状态转移次数阈值n1，需要的样本个数n2；

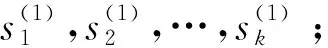
(3) Fort=1 ton1+n2

……

2.4 光伏出力序列的生成和修正

在多链马尔科夫模型学习了历史数据的状态转移规律的基础之上，进一步采用蒙特卡罗抽样方法生成离散状态序列，需要将其还原为光伏出力值。大气中云层的随机移动、聚集和消散给大气状态带来了瞬时扰动，为考虑这种随机波动特性，需要在状态序列中叠加白噪声序列ψ进行修正。若某光伏电站某一时刻所处的离散状态为s(t)，其所属的时段为第m个时期的第i个时段，那么该时刻的光伏发电功率为：

P(t)=Xm,i,min+(s(t)-ψ(t))hm,i

(8)

3 算例分析

为了验证多链马尔科夫模型对于考虑相关性光伏电站出力建模的有效性，文中采用了美国俄勒冈地区6个光伏电站及我国宁夏地区光伏电站出力的数据进行仿真测试。美国俄勒冈地区的光伏电站的分布于4个区域，如图3所示。

图3 美国俄勒冈地区光伏电站地区分布Fig.3 Diagram of regional distribution of photovoltaic power plants in Oregon, USA

3.1 光伏电站的相关性分析

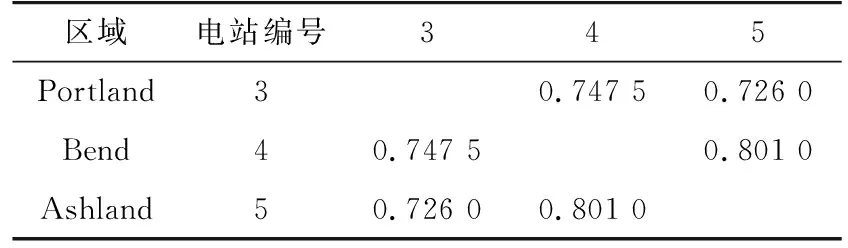
对本文选取的7个光伏出力观测数据序列进行相关性分析，其出力序列的互相关程度如表1所示。

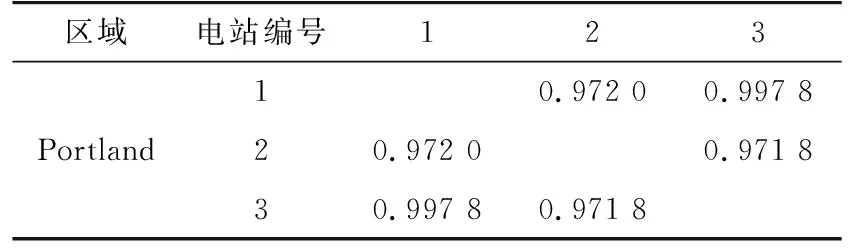
表1 光伏电站相关程度Tab.1 Correlation coefficients between PV power plants

(b) 算例2

(c) 算例3

从表1中可以看出，Portland地区的3个光伏电站出力序列的相关程度超过0.9，呈现高度相关关系；分布于Portland、Ashland和Bend 3个地区的光伏电站的出力序列的相关程度均大于0.7，其相关程度小于集中位于Portland的3个电站；Sheldon Village地区和我国宁夏地区光伏出力相关系数较小，由于两地区纬度相近，两地光伏电站的出力仍具有一定的相关性。显然，地理位置上越接近的光伏电站，地区上空的大气层状态之间的相互影响越大，其光伏出力序列的相关程度越强。

3.2 单链MCMC方法

采用单链MCMC方法对7个光伏电站的出力进行仿真模拟，离散状态数选取为20，仿真时间长度为10 a。光伏出力的极限转移矩阵约在1500～2000次达到收敛，设置状态转移次数的阈值为2000。

光伏出力序列的一般统计参数包括均值、标准差、概率密度函数和累积概率密度数。其中，概率密度函数和累计概率密度函数描述了光伏电站发电功率的长期概率分布。图4中给出了各个光伏电站预测序列的一般统计参数对比，可以看出，单链MCMC方法预测的光伏出力序列能够较好地继承历史序列的基本统计特性。

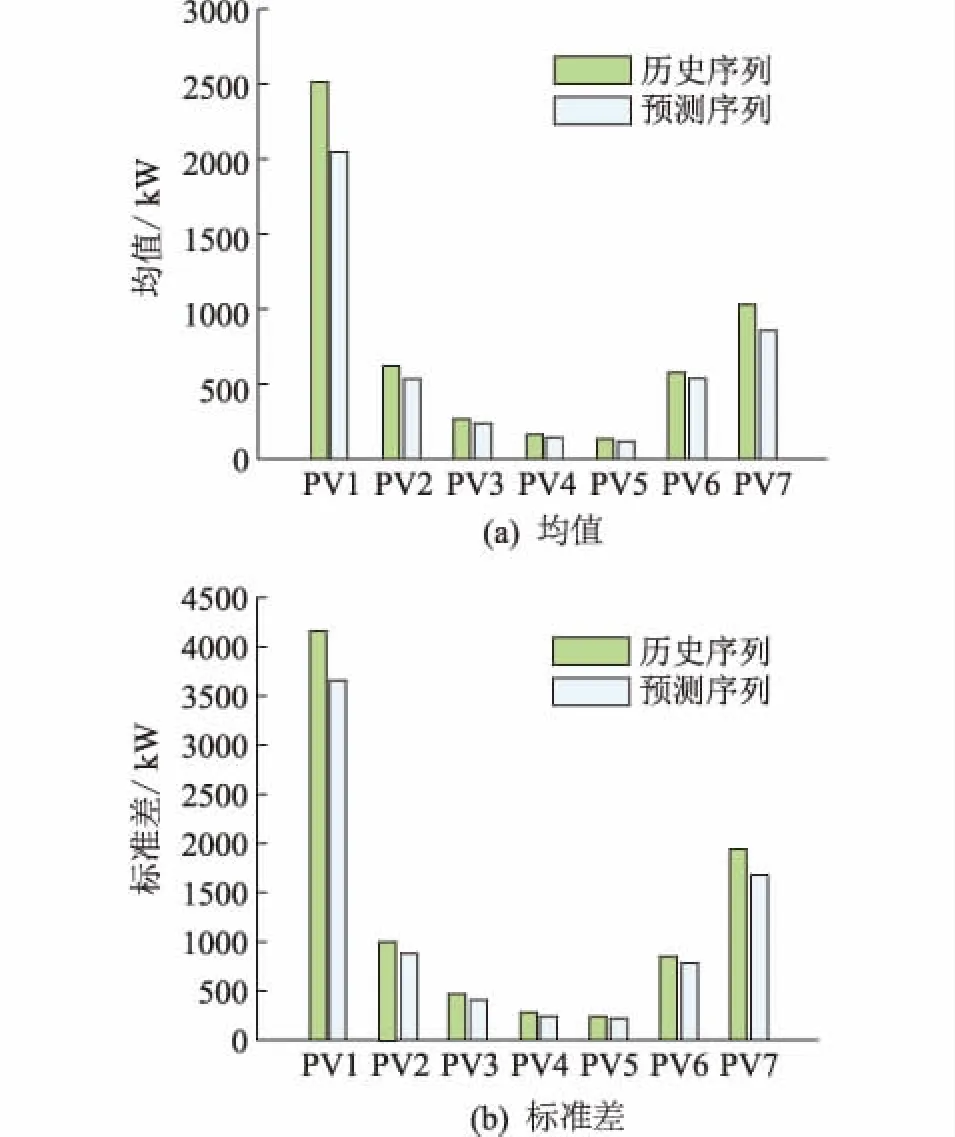
图4 单链方法下7个光伏电站原始/预测基本统计特性对比Fig.4 Comparison of basic statistical characteristics of historical and predicted time series of 7 PV plants outputs using single MCMC method

从图5中可以看出生成序列的概率密度分布和累计概率分布均和历史序列十分接近，说明单链MCMC方法能够较好地模拟历史序列的分布效果。

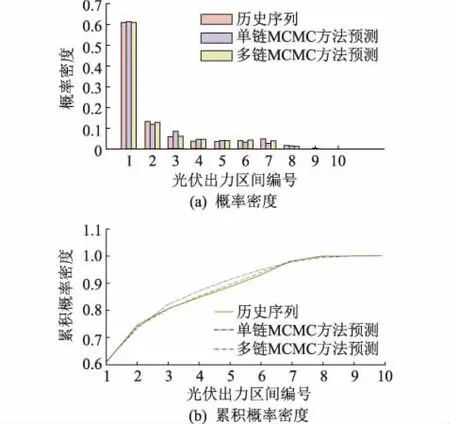
图5 生成光伏序列概率密度和累积概率密度对比Fig.5 Comparison of probability density and cumulative probability density between single and multi MCMC method

3.3 多链MCMC方法

3.3.1 一般统计参数对比

采用多链MCMC方法对3组光伏电站出力序列进行仿真，其生成序列的一般统计参数和单链方法的对比如图5和图6所示，将光伏出力范围等分为10个区间按从小到大的顺序编号为1-10。从图5可以看出，多链方法生成序列的概率密度和累积概率密度与历史序列更为接近，更能体现历史序列的统计特征。图6描述了两种方法所预测的序列相比于历史序列的平均绝对百分误差(MAPE)，从图6中可以看出，光伏电站之间的相关程度越高时，采用多链方法生成的预测序列的均值和标准差相较于历史序列的误差越小，能更好地维持历史序列的基本统计特性。但随着组间光伏电站出力的相关程度的降低，多链方法的预测精确度有所降低，可能是因为相关程度较低的光伏电站在地理位置上相距较远，大气和云层之间的影响也较小。总体上，考虑相关性的多链MCMC方法在描述光伏电站的出力特性上仍然优于原始的单链方法。

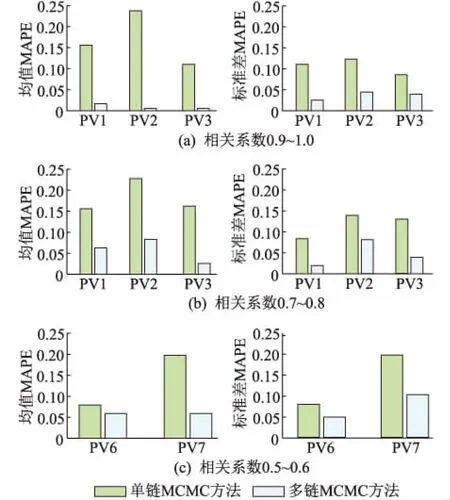
图6 单链/多链方法下不同相关水平的 光伏电站预测序列和历史序列的 基本统计参数对比Fig.6 Comparison of basic statistical characteristics of historical and predicted time series of PV plants outputs of different relevant levels between single and multi MCMC method

3.3.2 相关性参数对比

采用两种方法预测3组光伏电站的出力序列的相关系数对比如表 2所示。

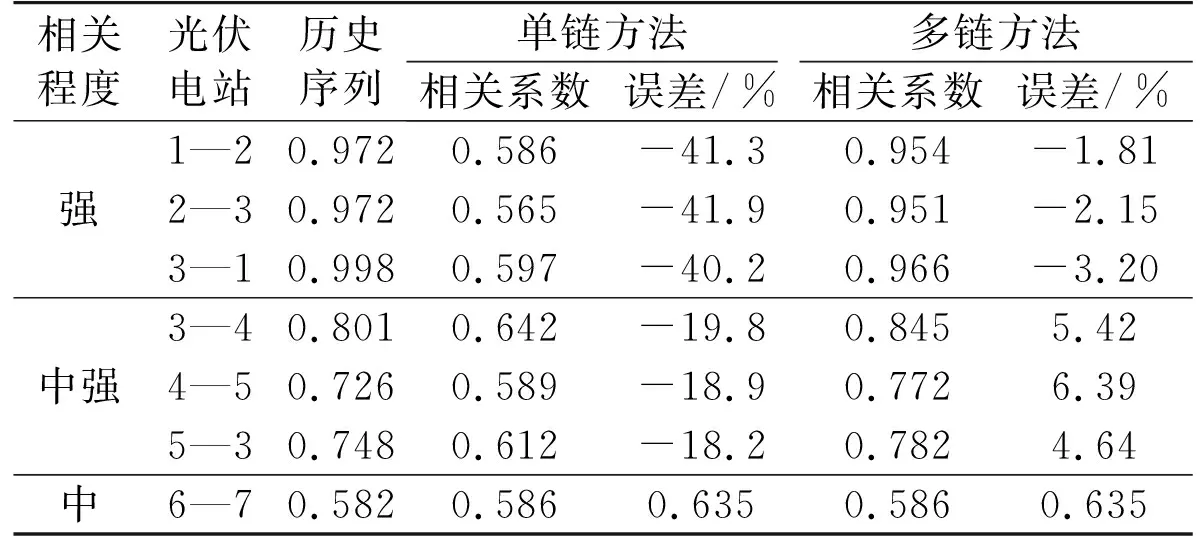
表2 单链/多链方法下不同相关水平的光伏电站 预测序列和历史序列的相关系数对比Tab.2 Comparison of correlation coefficients of predicted time series of PV plants outputs of different relevant levels between single and multi MCMC method

相关程度光伏电站历史序列单链方法多链方法相关系数误差/%相关系数误差/%1—20.9720.586-41.30.954-1.81强2—30.9720.565-41.90.951-2.153—10.9980.597-40.20.966-3.203—40.8010.642-19.80.8455.42中强4—50.7260.589-18.90.7726.395—30.7480.612-18.20.7824.64中6—70.5820.5860.6350.5860.635

从表2中可以明显看出，光伏电站之间的相关程度越高，多链方法所生成的预测序列保留原始序列之间相关性的效果越好。当光伏电站之间的相关系数较小时，单链方法和多链方法均能较好地继承历史序列之间的相关特性。这是因为光伏电站出力序列之间的相关程度由它们之间的地理距离决定，地理上相距越远的电站，其上空的大气状态之间的影响也越小，此时单链马尔科夫模型可以较好地刻画各地区大气状态的随机变化特性。而光伏电站之间的地理位置越接近时，它们的出力序列的相互影响越大，各光伏电站出力所对应的大气状态服从彼此之间的完全条件分布，因而此时考虑相关性的多链方法能够更好地分析各个光伏电站之间的相互影响因素。

统计方法中，自相关系数常用来表示时间序列的前后相关程度，其计算方法如式9所示：

(9)

式中：Xi为时间序列；μ和σ分别为该时间序列的均值和方差；k表示时延阶数。

单链方法和多链方法生成的预测序列的自相关系数对比如图7所示，可以看出，多链方法预测序列的自相关曲线与历史序列更加接近，能够较好地保留原序列的时间相关性。

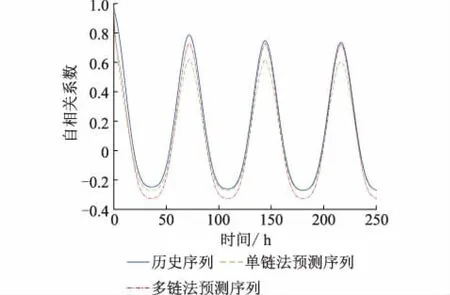
图7 两种方法光伏电站预测/ 历史序列的自相关系数对比Fig.7 Comparison of autocorrelation coefficients of predicted time series of PV plants outputs between single and multi MCMC method

4 结语

文中提出一种考虑多光伏电站出力相关性的光伏出力序列预测方法。将多个光伏电站的出力序列转化为反应大气特征的离散状态序列，辨识多条历史序列的状态转移规律，建立多条相互服从完全条件分布的马尔科夫链，对离散状态的随机波动特性进行修正后还原生成光伏出力序列。该多链MCMC方法应用于国内外7个具有不同相关程度的光伏电站功率序列生成，通过与历史数据和单链方法进行对比分析，得到以下结论：

(1) 基本统计特性上，当一组光伏电站之间的相关程度较高时，多链方法较单链方法所生成的光伏功率序列，在均值和标准差上与原始光伏功率序列更为接近，在概率分布上更接近于原始分布，且对于相关性越强的光伏电站模拟准确度越高。

(2) 相关特性上，多链方法在预测不同相关程度的光伏电站的出力序列时，均能较好地维持光伏电站之间的相关特性，而单链方法不适用于相关程度较高的多个光伏电站出力序列的组合预测。

(3) 文中的多链MCMC方法适用于不同相关水平的光伏电站出力序列的组合预测，能够继承原始序列的基本统计特性，有效地体现多个光伏电站出力水平之间相互影响的特点。