EHA半主动悬架自适应Smith预估时变时滞补偿控制

2018-12-12寇发荣许家楠

西安科技大学学报 2018年6期

寇发荣，李冬，许家楠，方涛

(西安科技大学机械工程学院，陕西西安 710054)

0 引言

半主动悬架在控制品质上接近于主动悬架[1-5]，且能耗低，因此越来越成为学者们研究的热点。电动静液压作动器(Electro Hydrostatic Actuator，EHA)是一种通过改变电机外接电阻而能改变作动器阻尼力的减振装置，具有功率密度大、调节范围广、易于模块化低等优点[6-8]，特别适合于半主动悬架控制领域。控制算法的研究使得半主动悬架的性能显著提升，但半主动控制时的时滞问题严重降低了悬架的控制品质，甚至导致系统发生失稳[9-10]。考虑到传感器采集并传输信号、控制律运算等环节的时滞非常小，通常只考虑EHA作动器的响应时滞[11]。

文献[12-17]基于Smith预估补偿控制策略设计了半主动悬架的时滞补偿控制器，验证了控制器的有效性，但都是基于临界时滞时间的补偿；实际悬架系统的时滞时间与临界时滞并不相同，且不可知，因此传统Smith预估补偿控制策略基于临界时滞的补偿方式不能达到较好的时滞补偿效果，即不能实现对时变时滞的补偿控制。

文中在传统Smith预估补偿控制的基础上，结合含时滞EHA悬架时滞的时变特性，设计了一种自适应Smith预估时变时滞补偿控制器，对含时滞的控制力进行自适应Smith补偿控制。通过建立含自适应Smith预估时变时滞补偿控制的EHA半主动悬架仿真模型，验证不同时滞时间下时滞补偿的有效性及相比传统Smith预估时滞补偿下的控制效果。

1 含时滞EHA半主动悬架动力学模型

1.1 EHA半主动悬架工作原理

EHA半主动悬架结构如图1所示。该半主动悬架主要由EHA作动器和螺旋弹簧构成，其中EHA作动器由无刷直流电机、液压泵、液压缸等构成。控制器根据反馈回来的信号计算出悬架此时所需的阻尼力，再通过改变电机回路的外接电阻阻值，进而改变电机的电磁转矩，并通过联轴器传递到液压泵，使得液压缸进、出油口的压力差作用于活塞而产生阻尼力，实现半主动控制。

图1 EHA半主动悬架结构Fig.1 Structure of semi-active suspension with EHA

1.2 含时滞1/4车辆2自由度悬架动力学模型

根据图1所示的EHA半主动悬架结构，建立了含时滞的1/4车辆2自由度EHA半主动悬架动力学模型，如图2所示。

图2 含时滞1/4车辆2自由度半主动悬架模型Fig.2 Model of quarter vehicle 2-DOF semi-active suspension with time delay

根据牛顿动力学定律，得到含时滞的1/4车辆2自由度半主动悬架动力学方程

(1)

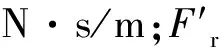
EHA作动器在半主动控制时所提供的阻尼力F分为基值阻尼力Fs和可控阻尼力Fr[13].基值阻尼力为作动器固有的黏滞阻力，所以时滞主要影响可控阻尼力的产生，且可以表示为[7]

(2)

式中Kr为电机电磁转矩系数,v·m/A；Kc为电机反电动势系数,v/r；ηv为液压马达容积效率；ηm为液压马达机械效率；A为活塞有效面积，m2；R为电机内阻与外接电阻阻值之和,Ω；b,ρ为液压油黏度和密度,m2/s,kg/m3；l,r为管路长度和半径,m；φ为局部压力系数；vg为活塞杆速度,m/s.

当悬架系统的时滞为τ时，作动器在t时刻提供的可控阻尼力为

(3)

(4)

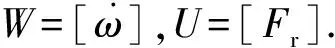
2 含时滞EHA半主动悬架的时变时滞

2.1 含时滞悬架系统的时变时滞

半主动悬架系统的临界时滞是由渐进稳定状态转变为不稳定状态的临界点，是表征时滞系统保持稳定状态时能够允许的最长时滞时间[13]。根据微分方程解的存在条件得到式(1)的非零特征方程为

(5)

系统出现失稳的临界条件是特征方程式(5)有纯虚根s=iω.将s=iω代入(5)中，分离实部和虚部并利用欧拉公式得到[18-20]

(6)

对式(6)进行求解，得到含时滞的EHA半主动悬架系统的临界时滞计算公式

(7)

由式(7)可知，EHA半主动悬架参数和可控阻尼范围确定时，当基值阻尼cs=1 000 N·s·m-1，得到可控阻尼对系统临界时滞的影响，如图3所示。

图3 可控阻尼与临界时滞的关系Fig.3 Relationship between controllable damping and critical time delay

从图3可以看出，当基值阻尼一定时，临界时滞随可控阻尼的增大而减小，当可控阻尼趋于无穷大时，临界时滞趋于某一个较小的值，但仍然存在。当可控阻尼足够小时，系统进入某一确定时滞稳定状态。

在小时滞时间下含时滞的悬架系统并不会发生失稳[12-13]，此时悬架系统的时滞时间小于临界时滞。由式(7)得，半主动悬架在控制过程中，其临界时滞在不断发生变化，实际的时滞时间也在小于临界时滞的范围内变化，即含时滞的半主动悬架的时滞具有时变特性，所以需要补偿的时滞时间也在不断变化。

2.2 时变时滞的自适应Smith补偿控制

Smith预估补偿控制策略的原理如图4所示，其基本原理是给系统的控制回路引入一个与原系统相并联的反馈环节[21-22]，即预估补偿器，由超越单元将被延迟的时间τ提前送入控制器，可以完全抵消时滞对系统的影响，但是Smith预估补偿控制策略只适用于定时滞的补偿控制，因为对于悬架系统，无法得到确定的时滞时间，也就无法给定需要补偿的时滞时间。

图4 Smith预估时滞补偿控制原理Fig.4 Principle of Smith predictive time delay compensation control

由于含时滞EHA半主动悬架在控制过程中时滞时间的时变性，导致时滞补偿模型也具有时变性，影响了时滞补偿的准确性。引入了自适应Smith预估时变时滞补偿控制策略[23-24]，其原理如图5所示。其中R(s)为控制器参考输入;Y(s)为系统输出；Gc(s)为悬架控制器模型；Gm(s)为理想的补偿模型;Gp(s)e-τs为实际有时滞的系统模型。

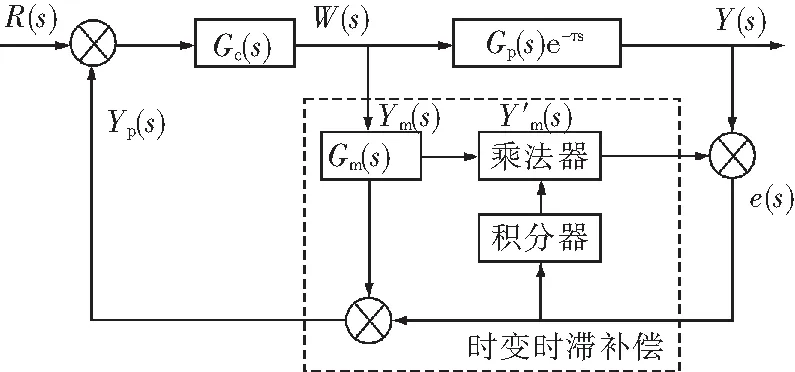
图5 自适应Smith预估时变时滞补偿控制原理Fig.5 Principle of adaptive Smith predictive time-varying delay compensation control

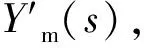
由图5对虚线框内的控制器进行分析得到下列各关系式

(8)

(9)

Yp(s)=e(s)+Ym(s)

(10)

Ym(s)=W(s)Gm(s)

(11)

由关系式(8)和(9)得

(12)

由式(12)得，当s→0时，e(s)=0，结合式(10)、(11)得到此时理想补偿模型的等效传递函数为

(13)

由式(13)可知，当时变时滞引起对象模型Gm(s)输出和实际模型Gp(s)输出不相等时，系统能自适应地调节对象模型的输出，即Gm(s)不断调节，使得对象模型Gm(s)和实际对象模型Gp(s)的输出之差在有限的时间内逼近零，即消除了时变时滞所引起的控制信号偏差。

3 EHA半主动悬架自适应Smith时滞补偿控制

EHA半主动悬架自适应Smith预估时变时滞补偿控制原理如图6所示。时滞导致悬架系统的实际控制力相比理想主动力有迟滞，用自适应Smith预估时变时滞补偿控制策略预估出此时含时滞控制力的补偿量，通过对两者求和得到时滞补偿后的控制力，再通过电阻求解环节得到作动器电机的外接电阻，进而作用于实际含时滞的EHA作动器。

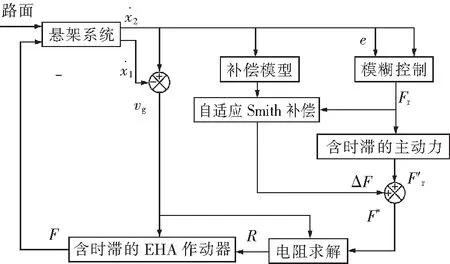
图6 自适应Smith时滞补偿控制原理Fig.6 Principle of adaptive Smith delay compensation control

3.1 EHA半主动悬架的模糊控制器设计

图7 EHA半主动悬架模糊控制器Fig.7 Fuzzy controller of semi-active suspension with EHA

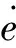
由于EHA作动器在半主动控制时不能对系统做正功，只能通过改变电机外接电阻阻值来改变可控阻尼力，所以当不考虑时滞时，可控阻尼力Fr(t)满足

(14)

式中 F(t)为模糊控制器求取的理想主动力,N；Fr(t)为理想半主动控制力,N.

3.2 自适应Smith时滞补偿控制器设计

根据图6得到EHA半主动悬架自适应Smith时滞控制系统如图8所示。

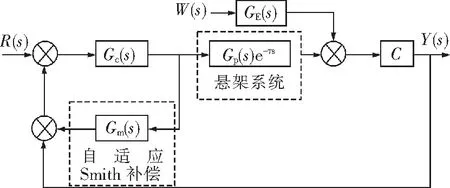
图8 EHA半主动悬架自适应Smith时变时滞补偿控制Fig.8 Adaptive Smith time-varying delay compensation control of semi-active suspension with EHA

在图8中，R(s)，W(s)分别为参考输入和路面激励的拉氏变换；Gc(s)为控制器控制力的拉氏变换;GE(s)=(sI-A)-1E，Gp(s)=(sI-A)-1B，C为输出矩阵。

由图8得系统输出Y(s)对路面激励输入W(s)的传递函数为

(15)

式(15)的分母中已经不含有纯滞后环节，满足Smith预估补偿算法的控制特点。

由式(13)得，自适应Smith时滞补偿控制器保证了补偿模型与实际模型的大致相同，因此式(15)可以写为

(16)

式(16)表明该系统闭环稳定，且忽略了时滞项，表明悬架系统的控制力得到了自适应Smith预估补偿控制。

模糊控制器输出悬架系统的理想主动力，可以改善悬架系统的动态性能，起作用的是悬架的控制器部分；而自适应Smith时滞补偿器是对时变时滞引起补偿模型偏差的改善，起作用的是时滞补偿控制器部分，两者结合在一起，可以发挥悬架控制的最大效果。

4 EHA半主动悬架时滞补偿控制仿真

根据图8所示的自适应Smith时变时滞补偿控制原理搭建了Simulink仿真模型，EHA半主动悬架的参数为：m2=250kg，m1=40kg，cs=1 300N·s/m，ks=13 000N/m，kt=117 000N/m，ηv=0.6，ηm=0.8，A=7.4×10-4m2，q=4×10-6m3，b=0.04m2/s，l=2m，ρ=900kg/m3，r=0.01m，φ=0.8.

为了分析自适应Smith预估时变时滞补偿控制下的悬架性能及对比传统Smith预估补偿下的控制效果，根据搭建的Simulink模型进行仿真分析。车辆以40km/h的速度行驶在C级路面上，EHA半主动悬架的时滞分别为0.05和0.1s时，仿真结果如图9～10所示。

表1给出了不同时滞时间下不同时滞补偿控制下的悬架性能的均方根值，表2给出了2种时滞补偿策略的控制效果。

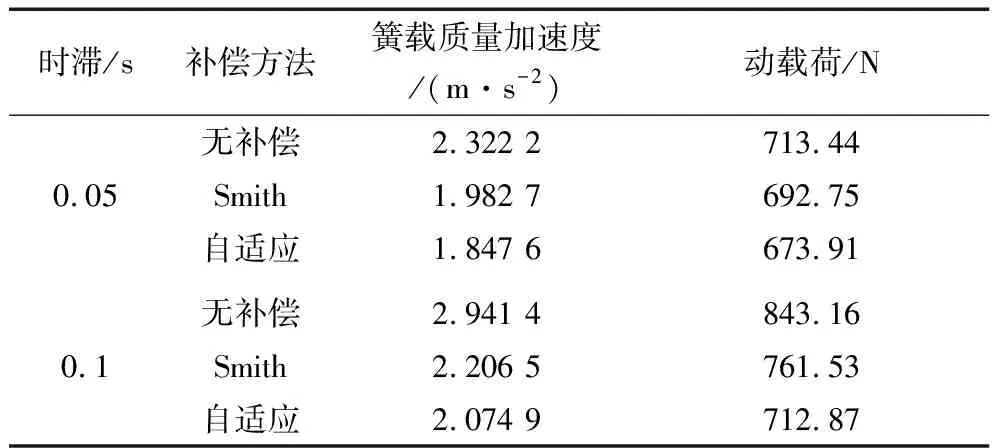
表1 不同补偿策略下悬架性能的均方根值Table 1 RMS value of suspension performance under different compensation strategies

图9 时滞为0.05 s时悬架性能对比Fig.9 Comparison of suspension performance with 0.05 s time delay

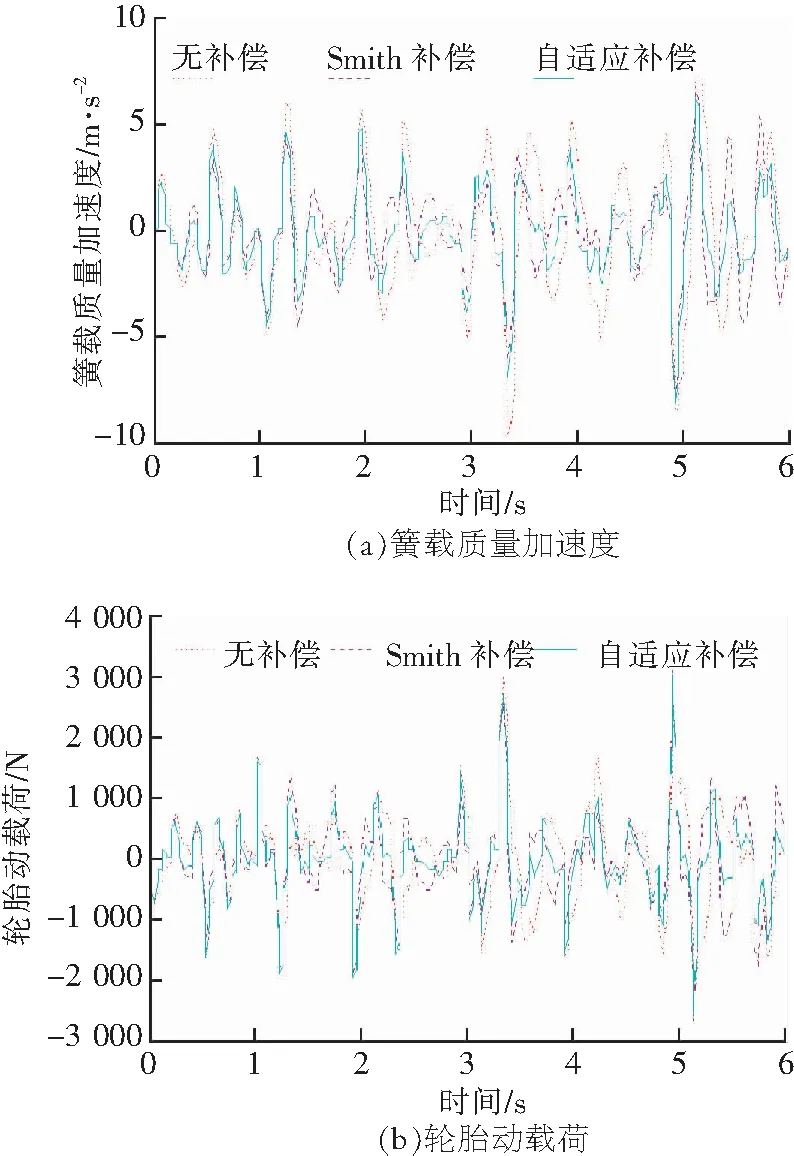
图10 时滞为0.1 s时悬架性能对比Fig.10 Comparison of suspension performance with 0.1 s time delay

从图9，图10，表1和表2可以看出，传统Smith预估补偿控制和自适应Smith预估补偿控制都能取得时滞补偿效果。相比于无时滞补偿控制下的半主动悬架，在0.05和0.1 s时滞时间下，传统Smith预估补偿控制下的悬架簧载质量加速度和轮胎动载荷的均方根值分别改善了14.6%，2.9%和25%，10%，自适应Smith补偿控制下的悬架簧载质量加速度和轮胎动载荷的均方根值分别改善了20.4%，5.5%和29.5%，15.5%.

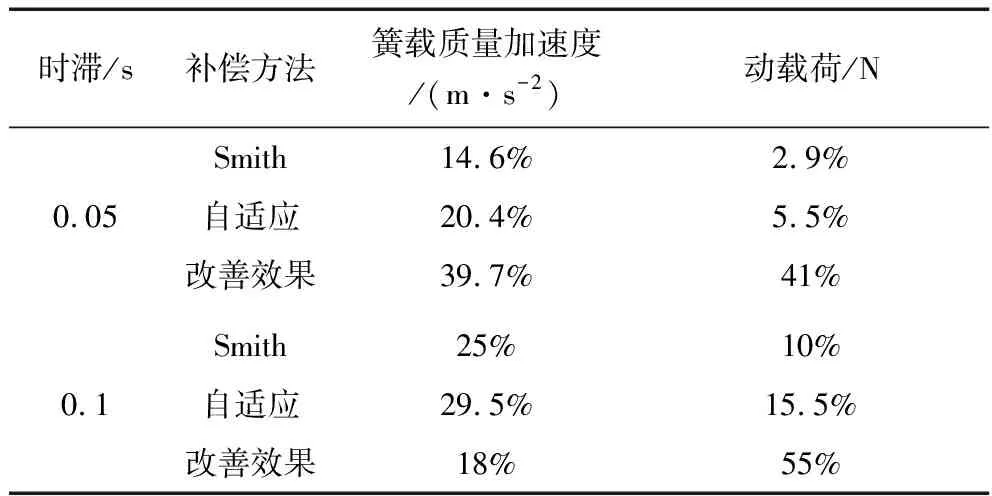
表2 不同补偿方法的补偿控制效果Table 2 Compensation control effects of different compensation methods

对于相同的时滞时间，自适应Smith预估时滞补偿控制下的控制效果相比传统Smith预估时滞补偿控制下分别提高了39.7%，41%和18%，55%.因此，当时滞时间改变时，即存在时变时滞时，自适应Smith预估补偿控制相比传统Smith预估补偿有更好的补偿控制效果。传统Smith预估补偿控制器时滞补偿时需要给控制器反馈需要补偿的时间，而自适应Smith预估时变时滞补偿控制器在补偿时不需要反馈补偿时间，更适合于含时变时滞悬架系统的控制。