深水气井测试水合物临界沉积粒径及敏感因素

高永海, 陈 野, 孟文波, 张 崇, 崔燕春, 王金堂, 孙宝江

(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.海洋水下设备试验与检测技术国家工程实验室, 山东青岛 266580; 3.中海石油(中国)有限公司湛江分公司,广东湛江 524057)

海洋具有丰富的油气资源,随着技术的发展,勘探开发逐渐由浅水区域转移向了深水区域,先后在西非、墨西哥湾、巴西等地海域展开了大规模的开发作业[1-3]。然而深水钻采的难度远高于常规钻采,其低温高压的环境也满足水合物生成条件,在能够提供充足的气与水的工况(例如气井携液)下,易诱导水合物颗粒生成、聚集[4]。水合物颗粒附着在井筒内壁上,逐渐堵塞管道,从而造成巨大的生产损失[5]。另外,在深水气井测试过程中,水合物堵塞井筒会干扰压力、流量等数据的计量,使其失去准确获取油气藏特性信息的意义,甚至导致生产测试无法进行[6]。为了解决以上问题,工业上普遍采用注入化学剂来抑制水合物生成[7],但该方法经济成本较高,且会在一定程度上影响测试、生产效果。由于水合物颗粒生成后,需要在满足一定条件下才能附着、沉积于管柱内壁造成堵塞,因此掌握管道内水合物颗粒沉积规律,对水合物堵塞精确预测具有重要意义和帮助[8]。水合物颗粒晶核的形成需要很长的诱导期,逸度差被认为是主要成核驱动力[9]。晶核一旦到达临界尺寸,就会快速生长[10]。Sloan等[11]提出成簇成核模型,将成核过程划分为可以用5个准基元反应来描述的4个阶段[12]。美国科罗拉多矿业学院研发了一套微机械测力装置,考察了颗粒间黏附力的影响因素,认为液桥力在颗粒间聚结时占据主导作用[13-15]。此外,固桥力同样是颗粒间作用力的主要来源,随着时间的推移,液桥力会逐渐向固桥力转化,形成更加稳定的、不可逆的固结作用[16]。宫敬等[17]借助 FBRM (颗粒粒度分析仪)和 PVM (颗粒录影显微仪)分析了水合物生成过程中颗粒/液滴的分布规律。刘海红等[18]以最大聚结粒径作为水合物聚结程度的标准改进了模型,并研究了油水界面张力等因素对聚结的影响规律。在以气相为主导的系统中,水合物沉积堵塞概念模型认为水合物首先在管壁表面成核,然后快速生长,由于流动等客观条件,水合物会从管壁脱落,至下游段沉积堵塞[19]。借助理想的假设条件,Nicholas等[20]提出了适用于层流的水合物颗粒移除模型。相比哈里伯顿等公司设计的摇晃式反应釜[21],水合物实验环路更接近管道内的实际流动环境,因此被广泛应用于水合物相变、运移、沉积等规律研究[22-27]。结合环路实验中天然气水合物在管道中的流动特点,以传统的固液双层流动模型为基础,将临界流动速度和临界床层高度作为天然气水合物浆稳定流动的判定标准,设计出了计算天然气水合物浆流型及流动参数的方法[28]。根据颗粒受力分析,赵鹏飞等[29]建立了油基天然气水合物颗粒管壁黏附动力学模型,定量探究了油包水乳状液中水合物颗粒在不同壁面环境下的黏附情况。基于水合物颗粒聚集动力学,引入群体平衡模型,建立三维几何模型进行联合求解,模拟了流速、水合物颗粒粒径及体积分数对管内水合物颗粒沉积特性的影响,证实了管道横截面处的水合物分布和粒径分布有较好的一致性[30]。已有的研究能够从热力学和动力学角度解释水合物颗粒在独立的理想环境中生成与运移机制,但缺乏针对具体工况,尤其是具体流型条件下水合物沉积规律的研究,难以为实际生产作业中管道内复杂的水合物沉积问题提出有效的预防建议[31]。笔者针对深水条件下以气相为主的环雾流工况,分析管道内水合物颗粒的受力情况,并结合具体的生产数据,计算水合物颗粒所受到的力矩,分析温度、压力、气相产量、液相产量及流通管径等因素对水合物沉积堵塞的影响规律。

1 管壁附近水合物颗粒受力分析

深水气井测试多为环雾流,在管壁附近会有一层薄液膜,其厚度随气相产量和液相产量而变化。简化水合物颗粒粒径和液膜厚度之间的浸入状态,即:①液膜厚度小于颗粒直径,称之为非浸入态(δ<2R),②液膜厚度大于等于颗粒直径,称之为浸入态(δ≥2R)。其中δ为液膜厚度,m;R为为水合物颗粒近似半径,m。

在非浸入态下,水合物颗粒与管壁间存在液桥力。在侵入态下,液桥力消失,固固黏附力将成为主要作用力[29]。由于管壁附近存在液相剪切应力,沉积颗粒在不断生长的过程中变得多孔而疏松,在剪切应力的作用下会发生新的破碎。破碎后的水合物颗粒一部分会脱离管壁,另一部分仍然会黏附在管壁上,直到形成稳定的水合物层。稳定的水合物沉积层形成之后,液膜会沿着水合物沉积层流动,开始新的沉积,不断加厚,直至堵塞管道[32]。

除此之外,颗粒在管壁附近还会受到范德华力、流速差异造成的径向升力、拖曳力、拖曳力矩、净重力、剪切力、固桥力等,如图1所示。

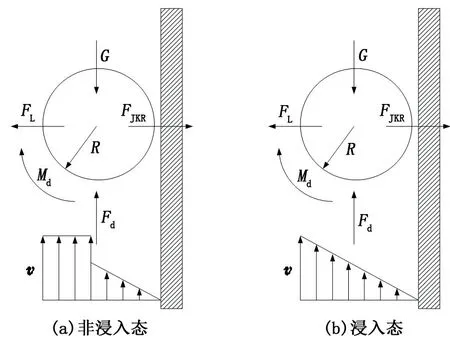
图1 管壁附近水合物颗粒受力示意图Fig.1 Diagram of forces on hydrate particle near pipe wall

气井测试过程中,水相在气相中呈现为分散相,水合物颗粒间液桥力的简化计算公式为

Fcap=2πRγglcosθ.

(1)

式中,Fcap为水合物颗粒间液桥力,N;γgl为气液界面张力,N/m;θ为接触角,(°)。

在颗粒向管壁的沉积过程中,颗粒与管壁间的固固黏附力成为主导,即

Fjkr=3πRγsl.

(2)

式中,Fjkr为颗粒与管壁间的固固黏附力,N;γsl为固液界面张力,N/m。

在管壁附近,颗粒所受拖曳力和力矩主要来源于气液相的流动。在颗粒浸入态下,采用黏性流动计算公式[33]:

Fd=1.700 9×6πμlRvc,

(3)

Md=0.943 993×8πμlR2vc.

(4)

式中,Fd为管壁附近水合物颗粒所受拖曳力,N;Md为管壁附近水合物颗粒所受拖曳力矩,N·m。

在颗粒非浸入态下,考虑颗粒在气液交界面的受力不同,将颗粒分为两部分,如图2所示。分别计算分相中的拖曳力,考虑颗粒球缺性对拖曳力的影响[34]。

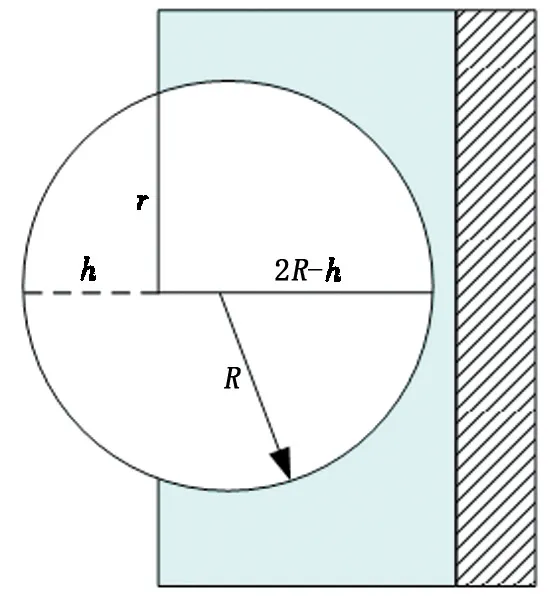
图2 水合物颗粒在气液交界面处的分部受力Fig.2 Forces of hydrate particles within gas and liquid phase

球体积和表面积分别为

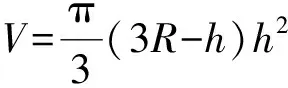
(5)

S=π(2Rh-h2)+2πRh=4πRh-πh2.

(6)

式中,V为球缺的体积,m3;r为球缺的底面半径,m;h为球缺的高度,m;S为球缺的表面积,m2。

其质心位置c为

(7)

则球缺等体积的球体直径为

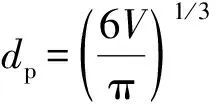
(8)

式中,dp为球缺等体积的球体直径,m。

考虑球缺的球度ψ,即球缺等体积的球体表面积与实际表面积的比值:

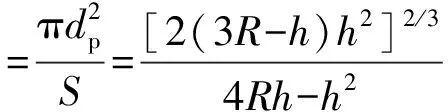
(9)

同时球缺的横向球度ψ⊥为与球缺等体积的球体横截面积与球缺沿流动方向的投影面积之比,即

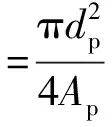
(10)

式中,Ap为球缺在流速方向上的投影面积,m2。对于不同部分,有

(11)

Ap2=πR2-Ap1.

(12)

在上述基础之上,以质心位置不变,计算分相中的拖曳力,即

(13)

Md1=0,

(14)

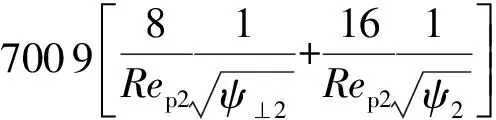
(15)

(16)

式中,Rep为质心处等体积球体在流体中的雷诺数;vc为球缺质心处的流速,m/s。

综上可得到总的拖曳力和附加力偶为

Fd=Fd1+Fd2,

(17)

Md=Md2+Fd1(c1+R-h1)-Fd2(c2+h1-R).

(18)

由于在径向上存在着速度梯度,颗粒在轴向运动的同时会受到径向的升力,而且在近壁面处速度梯度大,升力也随之增大。在颗粒浸入态下,管壁附近的层流区内,Saffman升力[35]为

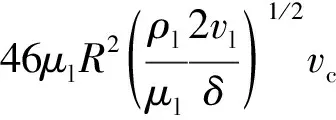
(19)

在颗粒非浸入态下,考虑到速度梯度在气相部分为零,升力仅为浸入液膜部分,考虑球缺性和线性分布流场的影响,即

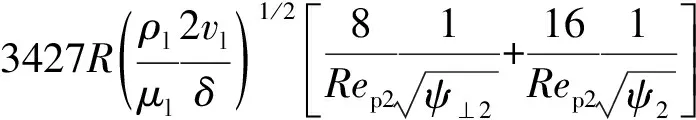
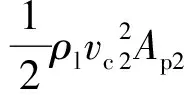
(20)

式中,Fl为Saffman升力,N;μl为液相黏度,Pa·s;R为水合物颗粒半径,m;ρl为液相密度,kg/m3;vl为液膜平均流速,m/s;δ为液膜厚度,m;vc为颗粒质心对应流速,m/s。

在颗粒完全不浸入液膜状态下,颗粒处于气相之中,Saffman升力为零。

由于管壁附近液相密度较大,相比于管壁中心部分,浮力大幅提高。在颗粒浸入液膜状态下,净重力为

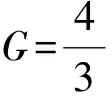
(21)

在颗粒非浸入态下,净重力为

(22)

式中,G为净重力,N;ρh、ρc、ρl分别是水合物、混合相和液体的密度,kg/m3。

由于液相黏度远大于气相黏度,液膜的存在会使管壁附近的剪切力变得很大。另外管壁附近速度梯度很大,加强了剪切作用。一旦水合物颗粒粒径足够大,就会被剪切破碎。

在颗粒不浸入液膜状态下,液相剪切力为零。在颗粒浸入液膜状态下,液相剪切应力或界面剪切应力成为主导,流速为线性变化,速度梯度很大,切应力为

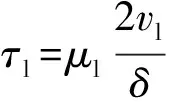
(23)

式中,τl为切应力,Pa。

两个水合物颗粒间的范德华力可以表示为

(24)

式中,Fvdw为范德华力,N;A为Hamaker常数,J,本文中取A=5×10-21J;h为颗粒之间距离,nm,取h=1.4 nm[36];R*为不同粒径的水合物颗粒谐波近似半径,m。

在水合物颗粒间相互接触之后,随着时间的增加,在接触点附近会逐渐开始生成水合物。研究表明,在颗粒接触30 s后会开始发生固结[16],而在实际测试过程中颗粒运移时间远大于30 s,因此水合物颗粒固结完全有可能发生。固桥力通过固桥破裂来计算:

Fsin=τtAi.

(25)

式中,Fsin为固桥力,N;τt为水合物抗拉强度,Pa,取τt=200 Pa(甲烷水合物)[37];Ai为水合物固桥在轴向方向的最小横截面积,m2。

由于水合物颗粒表面包裹有类液层,具有很好的静电消除能力,且接触之前会形成液桥,阻碍了颗粒间的直接碰撞,因此不考虑静电力和碰撞力对颗粒间作用的影响。

2 水合物颗粒临界沉积粒径判别方法

管道内壁通常并不完全光滑,其粗糙度为水合物颗粒沉积提供了很好的受力支点。由于颗粒在管壁上受到轴向力、径向力以及力矩,因此存在着3种沉积条件:

Fl≤Fjkr,

(26)

Fd-G≤f(Fjkr-Fl),

(27)

Md+(Fd-G)L1≤(Fjkr-Fl)L2.

(28)

式中,L1、L2为与表面粗糙度、颗粒表面粗糙度、颗粒变形等有关的参数,L1=0.6R、L2=0.2R[20];f为静摩擦系数。

从受力角度分析,水合物颗粒必须同时满足以下条件才能沉积到管壁上,即不升离、不滑动、不滚动,如图3所示。

定义滑动力Fs=Fd-G,静摩擦力Ff=f(Fjkr-Fl),移除力矩Mrem=Md+(Fd-G)L1,黏附力矩Madh=(Fjkr-Fl)L2,固桥力矩Msin=(Fsin-Fl)L2。以此为基础,分析计算流通直径70 mm、气相流量300 000 m3/d、液相流量15 m3/d、温度15 ℃、压力25 MPa条件下,不同沉积方式下水合物颗粒所受的作用力见图4。可以看出,随着颗粒粒径的增大,水合物颗粒所受到的各作用力都会相应增大,但增大幅度不同。

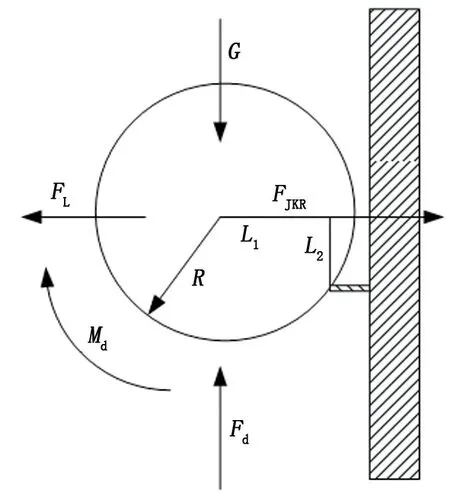
图3 管壁附近颗粒沉积受力分析Fig.3 Analysis of forces on hydrate particle near the wall

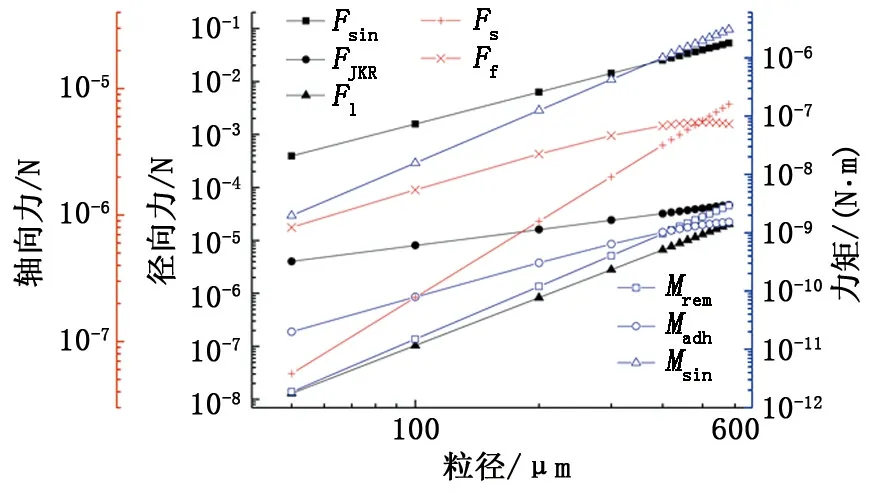
图4 不同沉积方式下水合物颗粒所受的作用力Fig.4 Force of particle size of hydrate with different deposition methods

根据式(26)～(28)的判别标准,分析表明,该工况下3种不同的沉积方式都存在着对应的沉积粒径。其中径向升离的临界粒径约为600 μm(即颗粒粒径约600 μm时,Fl=Fjkr),滑动脱离的临界粒径约为500 μm(即颗粒粒径约500 μm时,Fd-G=f(Fjkr-Fl)),而滚动脱离的临界粒径约为430 μm(即颗粒粒径约430 μm时Md+(Fd-G)L1=(Fjkr-Fl)L2)。因此从颗粒受力角度来研究,临界沉积粒径最小的滚动脱离是最容易发生的方式,即颗粒沉积的临界粒径由黏附力矩和移除力矩的平衡来控制。

当颗粒沉积后发生固化,其固化力矩大于移除力矩4个量级,无法再被移除,即水合物沉积一旦发生,除剪切破碎外,将不会再以升离、滑脱、滚动等方式从壁面移除,即具有一定的不可逆性。基于以上认识,水合物颗粒沉积的主要方式由不发生滚动的临界粒径决定,可以以该方式作为沉积判别标准。

3 临界沉积粒径敏感性因素

温度和压力是影响水合物颗粒生成与聚集的关键因素。除此之外,在实际工况条件下,附着于管壁附近的液膜厚度影响着作用于水合物颗粒的黏附力,而管道内产气速率影响着作用于水合物颗粒的剪切作用强度。同时,随着沉积的不断发生,管道内流通管径的变化也会改变流体流速,从而影响水合物颗粒的沉积。因此将以上参数作为敏感性因素,分析相应的水合物颗粒临界沉积粒径。

3.1 温度对水合物颗粒临界沉积粒径的影响

模拟产气量300 000 m3/d、产水量15 m3/d、压力25 MPa、管径70 mm时,不同温度条件下水合物颗粒所受的移除力矩与黏附力矩见图5(a)。可以看出,当其他因素保持不变时,温度升高,水合物颗粒所受的移除力矩和黏附力矩均减小,且水合物颗粒粒径越大,影响幅度越明显。当水合物颗粒粒径大于100 μm后,对比曲线可知,温度对移除力矩的影响逐渐减小,而对黏附力矩的影响则相对剧烈。其主要原因是黏附力矩的主要作用力为固固黏附力,与水合物-水界面张力成线性关系,而温度对界面张力的影响较大。因此黏附力矩随温度变化的幅度较明显。

为更加方便、直观地进行对比,对坐标轴(粒径、力矩)进行了对数化处理,结果见图5(b)。可以看出,随着水合物颗粒粒径的增大,移除力矩与黏附力矩之间的差值首先不断变小;而相交后则趋于变大,说明粒径超过临界沉积值后,移除力矩会比黏附力矩越来越大。二者的交点,即特定工况下对应的水合物颗粒临界沉积粒径。在模拟温度范围内,其水合物颗粒临界沉积粒径范围为350～450 μm。低于临界沉积粒径时,水合物颗粒所受的黏附力矩大于移除力矩,满足沉积条件，而高于临界沉积粒径时,水合物颗粒所受的黏附力矩小于移除力矩,不再发生沉积。

保持其他条件不变,流通管径分别为60、70、80 mm时,对黏附力矩与移除力矩的所有交点,即水合物颗粒临界沉积粒径进行比较,如图6所示。不同管径所对应的曲线均表明温度越高,水合物颗粒临界沉积粒径越小,即沉积过程越缓慢;反之,临界沉积粒径越大,沉积过程越剧烈。

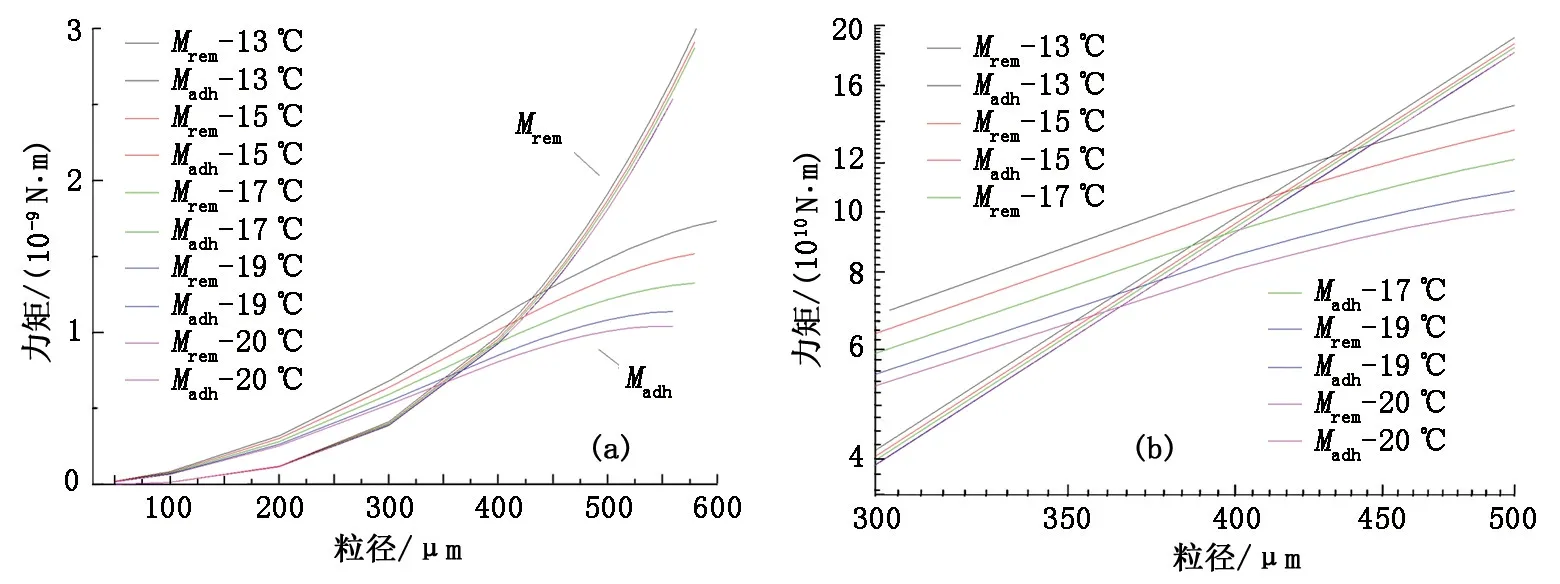
图5 不同温度条件下水合物颗粒所受力矩随粒径变化Fig.5 Hydrate particle moment changes with its size under different temperature

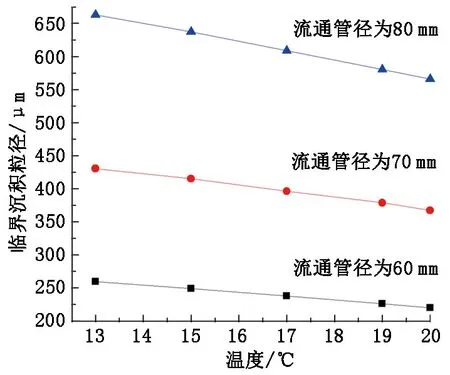
图6 流通管径内温度对临界沉积粒径影响Fig.6 Influence of temperature on critical deposition size

3.2 压力对水合物颗粒临界沉积粒径的影响

模拟产气量300 000 m3/d、产水量15 m3/d、温度15 ℃、管径70 mm时,不同压力条件下水合物颗粒所受的移除力矩与黏附力矩见图7。可以看出,当温度和产量等其他因素保持不变时,压力升高水合物颗粒所受的移除力矩减小而黏附力矩增加，且水合物颗粒粒径越大,压力对力矩影响的幅度越明显。这与气体的可压缩性相关,随着压力的增大,气相被不断压缩,密度和黏度都会增大,导致气相体积流量减小,整体流速降低,对液膜的剪切作用也会变弱,移除力矩降低;同时,径向速度梯度降低,Saffman升力减小,黏附力矩增大。与温度相反,压力对水合物颗粒所受黏附力矩的影响要小于对移除力矩的影响。在颗粒粒径大于300 μm后,黏附力矩与移除力矩随压力变化的幅度均较为明显。

对不同管径工况下即水合物颗粒临界沉积粒径(即黏附力矩与移除力矩的交点)进行比较,结果见图8。可以看出,不同管径所对应的曲线均表明压力越高,水合物颗粒临界沉积粒径越大,即能够沉积的颗粒会越来越多,沉积速率变大,沉积堵塞风险升高。

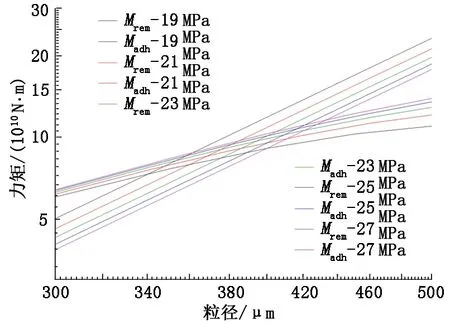
图7 不同压力条件下水合物颗粒所受力矩随粒径变化Fig.7 Moment changes with particle size under different pressure

图8 流通管径内压力对临界沉积粒径的影响Fig.8 Influence of pressure on critical deposition size

3.3 气相产量对水合物颗粒临界沉积粒径的影响

在水合物预测区域内,产气量为200 000～500 000 m3/d。模拟产水量15 m3/d、温度15 ℃、压力25 MPa、管径70 mm时,不同气相产量条件下水合物颗粒所受的移除力矩与黏附力矩,结果见图9。可以看出,其他因素保持不变时,气相流速增大,移除力矩有明显增加,黏附力矩有所减小。其主要原因为气相流量的增加会使液膜内流速增大,液膜厚度减小,液膜内速度梯度增大,Saffman升力增加,因此在一定程度上削弱了黏附力矩,计算条件下移除力矩与黏附力矩的交点主要发生在颗粒粒径为200～800 μm。

图9 不同气相产量下水合物颗粒所受力矩随粒径变化Fig.9 Moment changes with particle size under different gas flow rate

保持其他条件不变,分别对流通管径为60、70、80 mm的水合物颗粒临界沉积粒径进行分析,如图10所示。不同管径所对应的曲线均表明随着气相产量的增加,水合物颗粒临界沉积粒径逐渐减小,且随着流通管径减小而减小。另外,气相产量对水合物颗粒临界沉积粒径的影响较大,在流通管径为70 mm下,水合物颗粒临界沉积粒径变化范围约为700 μm,远高于温度(水合物颗粒临界沉积粒径变化范围约80 μm)和压力(水合物颗粒临界沉积粒径变化范围约100 μm)对水合物颗粒临界沉积粒径的作用程度。气相流速对颗粒沉积具有直接而关键的影响,适当提高流速可以降低水合物沉积速率,可以在一定程度上缓解水合物沉积堵塞。

图10 流通管径内气相产量对临界沉积粒径的影响Fig.10 Influence of gas production on critical deposition size

3.4 液相流量对水合物颗粒临界沉积粒径的影响

在水合物预测区域内,模拟产气量300 000 m3/d、温度15 ℃、压力25 MPa、管径70 mm时,不同液相流量条件下水合物颗粒所受的移除力矩与黏附力矩,结果见图11。可以看出,当其他因素保持不变时,随液相流量增加,移除力矩减小,而黏附力矩增加。液相流量的增加会使液膜变厚,液膜内速度梯度降低,同等条件下颗粒所受拖曳力和Saffman升力都会减小,故而移除力矩减小,黏附力矩增加。

图11 不同液相产量下水合物颗粒所受力矩随粒径变化Fig.11 Moment changes with particle size under different liquid flow rate

图11中移除力矩与黏附力矩的交点主要发生在颗粒粒径为320～460 μm的区间内。流通管径为60、70、80 mm时,所对应的曲线均表明液相流量增加,临界沉积粒径增大,如图12所示。可以看出,随着液相产量增加,液膜内平均流速增加,但液膜厚度的增大速度比流速更显著,故而液膜内速度梯度是降低的,液膜内剪切作用减弱。另外,在流通管径为70 mm下,水合物颗粒临界沉积粒径变化范围约为120 μm,说明液相流量的影响不如气相流量,对控制水合物沉积堵塞的作用效果有限。

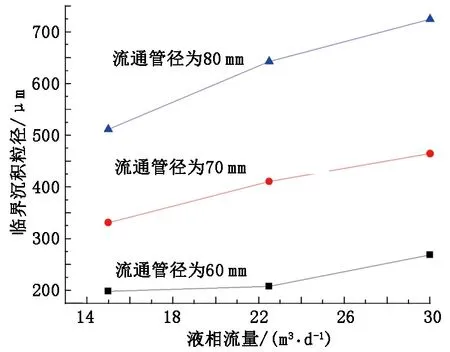
图12 液相流量对临界沉积粒径的影响Fig.12 Influence of liquid production on critical deposition size

3.5 流通管径对水合物颗粒临界沉积粒径的影响

随着管壁水合物沉积层厚度不断增长,井筒内流通管径越来越小,导致实际流速越来越大,反过来影响水合物颗粒的沉积过程。模拟产气量300 000 m3/d、产水量15 m3/d、温度15 ℃、压力25 MPa时,不同流通管径(40～114.3 mm)条件下水合物颗粒所受的移除力矩与黏附力矩,如图13所示。

图13 不同流通管径下水合物颗粒所受力矩随粒径变化Fig.13 Moment changes with particle size under different flow diameter

由图13可知,在模拟的粒径范围内,流通管径为100和114.3 mm的黏附力矩曲线始终高于移除力矩曲线,所有的水合物颗粒都会沉积。尽管黏附力矩曲线与移除力矩曲线逐渐靠拢,当颗粒粒径足够大时应该会相交,但也能够说明在实际作业的初始阶段,管道内水合物沉积堵塞现象是容易发生的。

随着水合物沉积层厚度的不断累积,流通管径进一步减小,移除力矩不断增大,而黏附力矩相对减小,直到两者相等,达到临界沉积粒径。在流通管径90 mm时,临界沉积粒径约为900 μm。将不同流通管径条件下黏附力矩与移除力矩的所有交点,即各流通管径所对应的水合物颗粒临界沉积粒径进行比较,如图14所示。根据曲线可知,随着流通管径不断变小,临界沉积粒径也会不断减小,水合物颗粒沉积趋于缓慢,直至完全堵塞井筒。

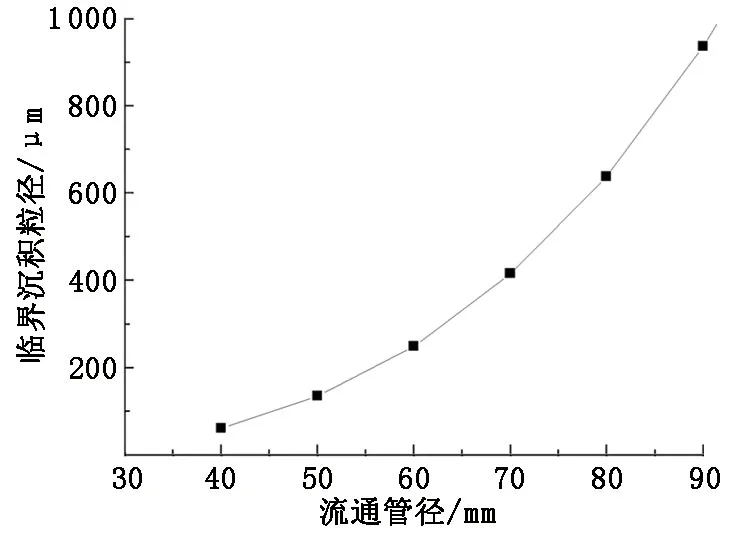
图14 流通管径对临界沉积粒径的影响Fig.14 Influence of flow diameter on critical deposition size

4 结 论

(1)管壁附近水合物颗粒主要受径向升力、固固黏附力和拖曳力作用,必须同时满足不升离、不滑动、不滚动才能沉积到管壁上。随着颗粒粒径的增大,水合物颗粒所受到的各作用力都会相应增大。但各作用力的增大幅度不同,使得水合物颗粒有可能从管壁脱离。

(2)径向升离的临界粒径约为600 μm,滑动脱离的临界粒径约为500 μm,而滚动脱离的临界粒径约为430 μm,滚动脱离最容易发生,颗粒临界沉积粒径主要是由黏附力矩和移除力矩的平衡来控制。

(3)温度、气相产量与水合物颗粒沉积粒径呈负相关,压力、液相流量、流通管径与水合物颗粒沉积粒径呈正相关。其中不同气相产量对应的水合物颗粒临界沉积粒径变化幅度最大,说明它的影响作用明显强于其他敏感性因素。

(4)在实际生产作业的初始阶段,井口附近水合物沉积的风险最高。随着沉积的不断发生,管道的有效流通内径越来越小,使水合物颗粒临界沉积粒径随之变小。合理调节井内温度、压力、气相产量、液相流量,可以在一定程度上改变水合物颗粒临界沉积粒径的大小,控制水合物沉积速率与沉积层厚度,从而实现预防管道堵塞、保障生产安全的目的。