主成分分析与因子分析在儿童心脏生长发育中的应用

孙玲玲

【摘 要】主成分分析法与因子分析法都是寻找各变量之间的共性因素的统计方法。本文通过案例研究，分别用主成分分析法与因子分析法对案例进行分析，得出两种方法之间具有密切的联系。

【关键词】主成分分析；因子分析；多元统计方法；公因子

中图分类号： G642.0 文献标识码： A 文章编号： 2095-2457（2018）21-0226-002

DOI：10.19694/j.cnki.issn2095-2457.2018.21.104

【Abstract】The principal component analysis and the factor analysis are statistical methods to find the common factors among the variables.In this paper，we study the case by the methods of principal component analysis method and the factor analysis method，and we obtain that there are close relationship between the two methods.

【Key words】Principal component analysis；Factor analysis；Multiple statistical methods；Common factor

0 前言

主成分分析法与因子分析法是医学研究中的常用统计分析方法，其中王文博[1]探讨了多指标综合评价中主成分分析与因子分析方法中的比较，龚燕冰[2]研究了因子分析法在临床中的应用，林海明[3]、熊志斌[4]研究了主成分分析法在综合评价中应注意的问题。本文主要应用两种分析方法得出儿童心脏生长发育的各项指标中起主要作用的指标。

1 主成分分析法与因子分析法的介绍

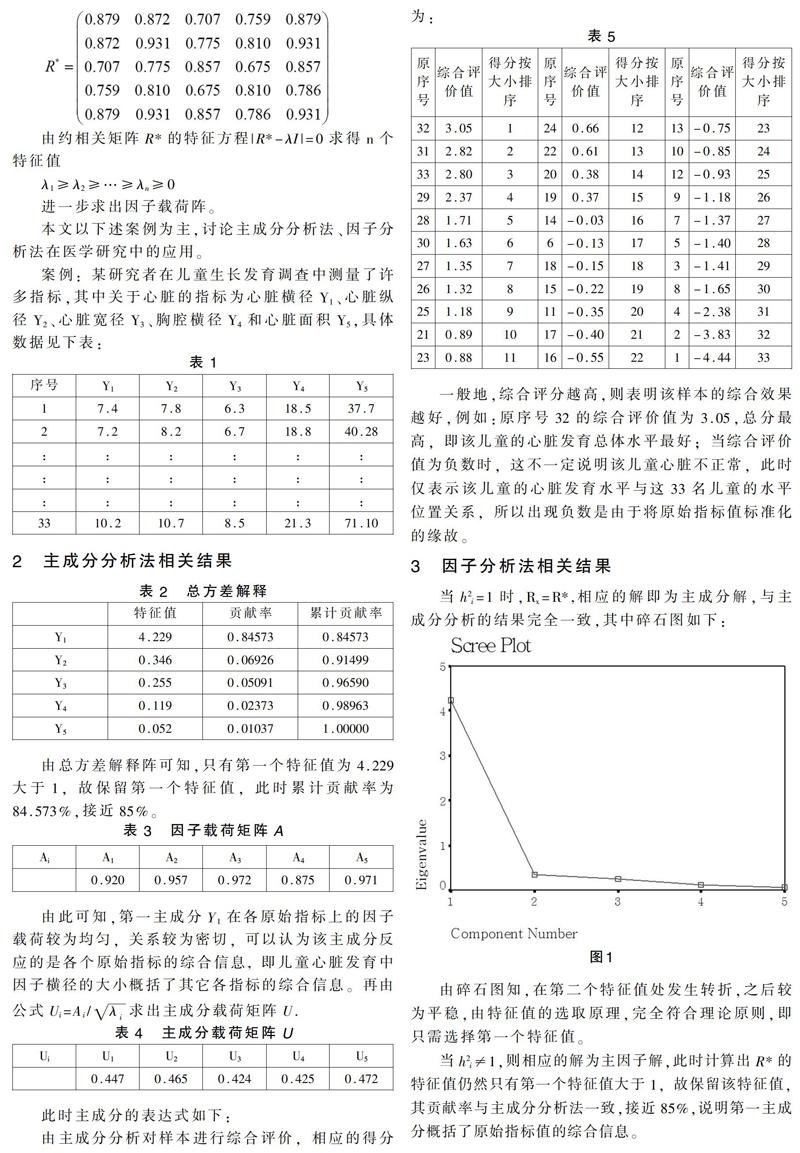
主成分分析是运用降低原始变量维度的方法，将n个变量指标化为p个互不相关的综合指标的统计方法，其中0

设有n个指标Y1，Y2，…，Yn欲寻找可以概括这几个指标的主要信息综合指标W1，W2，…，Wn即寻找一组常数ki1，ki2，…，kin，i=1，2，…，n使这n个指标的线性组合：

因子分析是在主成分分析的基础上进行推广，在（1）式中，找出起主要作用的综合因子，使得这些因子在每个原始指标上的公共度都达到较为满意的水。因子分析法仍需对各原始数据标准化，求出相关系数矩阵RX如下：

将相关矩阵的对角元换为公因子方差h2i即得约相关矩阵R*，此时当h2i=1，则Rx=R*，相应的解即为主成分解，与主成分分析的结果完全一致，此时的主成分即是公因子；若h2i≠1，则相应的解为主因子解，此时需要先估计的h2i值，一般地，h2i取RX第i行上各相关系数绝对值的最大值（主对角元除外），即得约相关矩阵

进一步求出因子载荷阵。

本文以下述案例为主，讨论主成分分析法、因子分析法在医学研究中的应用。

案例：某研究者在儿童生长发育调查中测量了许多指标，其中关于心脏的指标为心脏横径Y1、心脏纵径Y2、心脏宽径Y3、胸腔横径Y4和心脏面积Y5，具体数据见下表：

2 主成分分析法相关结果

由总方差解释阵可知，只有第一个特征值为4.229大于1，故保留第一個特征值，此时累计贡献率为84.573%，接近85%。

此时主成分的表达式如下：

由主成分分析对样本进行综合评价，相应的得分为：

一般地，综合评分越高，则表明该样本的综合效果越好，例如：原序号32的综合评价值为3.05，总分最高，即该儿童的心脏发育总体水平最好；当综合评价值为负数时，这不一定说明该儿童心脏不正常，此时仅表示该儿童的心脏发育水平与这33名儿童的水平位置关系，所以出现负数是由于将原始指标值标准化的缘故。

3 因子分析法相关结果

当h2i=1时，Rx=R*，相应的解即为主成分解，与主成分分析的结果完全一致，其中碎石图如下：

由碎石图知，在第二个特征值处发生转折，之后较为平稳，由特征值的选取原理，完全符合理论原则，即只需选择第一个特征值。

当h2i≠1，则相应的解为主因子解，此时计算出R*的特征值仍然只有第一个特征值大于1，故保留该特征值，其贡献率与主成分分析法一致，接近85%，说明第一主成分概括了原始指标值的综合信息。当用因子分析法求得的公因子的专业意义不清楚时，可以通过因子旋转的方法来解决，此案例中，因子分析的结果显示公因子第一主成分已经能够很好地反映个指标所包含的大部分信息，故无需做因子旋转。

4 结语

由以上分析可知，因子分析是在主成分分析的基础上进行推广，因子分析的解与约相关矩阵由关，当约相关矩阵取法不唯一时，因子分析的解也不唯；当约相关矩阵与相关矩阵相同时，因子分析法的解与主成分分析法的解完全一致。两种方法都能很好地反映各指标的综合信息，是医学研究的重要统计分析方法。

【参考文献】

[1]王文博，陈秀芝.多指标综合评价中主成分分析和因子分析方法的比较[J].统计与信息论坛，2006（05）：19-22.

[2]龚燕冰，罗增刚，高思华，倪青，易丹辉，谢雁鸣，王永炎.运用因子分析方法探索2型糖尿病证候要素及其靶位特征[J].中医杂志，2011，52（13）：1100-110

[3]林海明，杜子芳.主成分分析综合评价应该注意的问题[J].统计研究，2013，30（08）：25-31.

[4]熊志斌.基于非线性主成分分析的信用评估模型研究[J].数量经济技术经济研究，2013，30（10）：138-150.

[5]赵耐青.医学统计学.第2版.人民卫生出版社，2005：423-440.