中国南海张力腿平台的波浪水池模型试验与数值分析对比
2018-12-10杨小龙秦立成
王 飚, 杨小龙, 秦立成, 王 磊
(1. 海洋石油工程股份有限公司, 天津 300451; 2. 上海交通大学 高新船舶与深海开发装备协同创新中心(船海协创中心), 上海 200240)
0 引 言
我国南海蕴藏着丰富的深海油气资源,发展适合南海深水油气开发的平台结构成为近年来的研究热点。张力腿平台(Tension Leg Platform, TLP)由于其具备适用水深范围广,耐波性能优良,可干式采油等优点,在国外得到了广泛应用。近2年,国内对TLP的研究逐渐从科研走向生产,未来几年,极有可能采用TLP进行南海油气的开发。TLP的波浪响应本身具有强非线性,在浅水中则表现更加明显,这使得对其进行准确的数值预报更为困难,工程上通过水池模型试验对数值模拟的结果进行修正[1-13]。
飓风卡特里娜和丽塔袭击了墨西哥湾以后,API [API RP 2T]对工程设计推荐了新的环境准则和更为严格的设计标准[14],海洋工程的参与者也有机会可以回顾审查过去的设计原则并关注未来的项目[15]。受益于DeepStar JIP,对包括TLP在内的浮式结构物的分析和模型试验都进行了进一步的研究[16]。为准确预报TLP的高阶波浪响应,本文在上海交通大学海洋工程深水国家重点实验室进行了相关的水池模型试验研究,水池长50 m,宽40 m,最深处水深10 m,设有可移动的假底来模拟不同的水深。采用1∶60的缩尺模型。本文描述了TLP船体模型的建模,环境校准及试验准备的过程,对试验结果进行分析并与数值预报进行对比,最后提出了一套满足工程实际的响应数值预报方法。
1 模型试验准备
1.1 船体建模
TLP船体包括4个立柱,立柱底部通过4个旁通相连接。平台由8根张力腿筋腱系泊,每个立柱上各连接2根。在原型比尺下,筋腱连接在船体靠近立柱底部的位置,距离基线约4 m。
TLP的主尺度和质量分布见表1和表2。图1展示了制作完成的下浮体模型。

表1 TLP原型和模型的主尺度 m
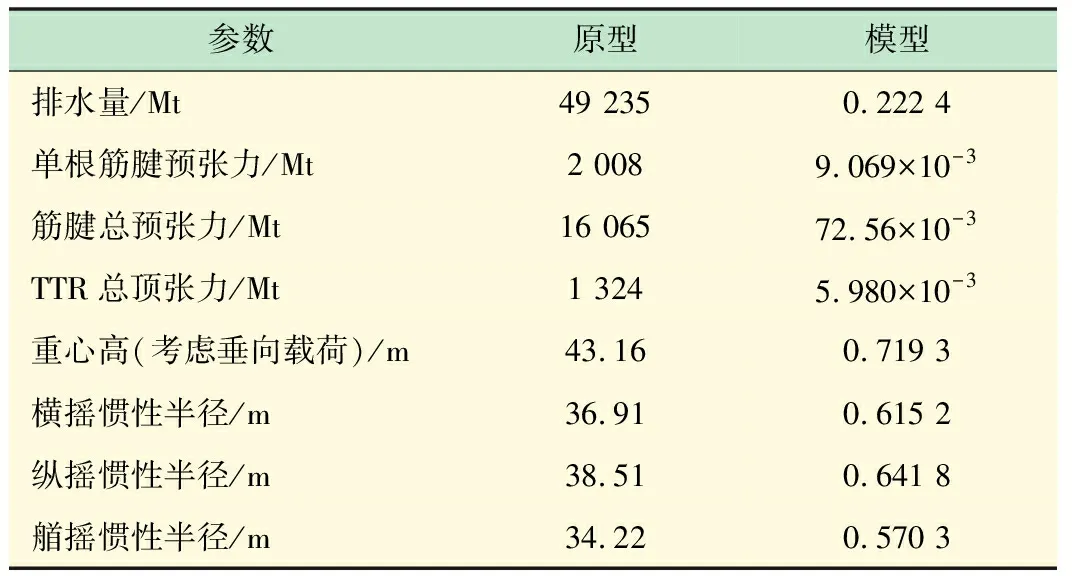
表2 TLP原型和模型的质量信息

图1 带附属结构物的试验模型
1.2 腿筋腱和TTR建模
每根筋腱的模型包括上下两部分的铝管和中间的弹簧。铝管的直径和壁厚需要计算保证模型相似,模型外径和原型外径需要保证几何相似,而中空铝管内部需要进行配载来保证质量相似。铝管内部使用了平均分布的钢丝进行配载来保证张力腿筋腱在水中的湿重相似。铝管的各个部分需要在模型试验期间保证水密性。
考虑到模型试验中相对较浅的水深,筋腱模型的模型精度会对张力腿张力响应产生显著影响,因此筋腱模型的相关特性需要在水池试验前仔细校准标定,如湿重、轴线刚度等,同时要对其进行水密性试验以避免试验过程中铝管发生渗水。

图2 铝管及中间的连接弹簧
波浪水池模型试验中,原型的12根立管简化模拟为4根,简化模型中考虑了立管张紧器的影响。和张力腿筋腱模型类似,等效的TTR模型进行了全尺度模拟,没有进行截断。同样使用合适直径及壁厚的铝管进行模拟。这些铝管进行了水密处理以保证在试验中浮力不发生变化。配载重量置于铝管内部以保证湿重相似。张力弹簧布置在两段铝管中间以模拟立管的轴向刚度(见图2)。立管模型的特征参数,包括湿重,轴向刚度等需要在试验前进行校准标定。
1.3 环境模拟和校准
TLP平台原型所处水深为404.69 m,折合模型水深为6.745 m, 试验中用到的海况见表3(Jonswap 谱 gamma值 = 2.4)。海况条件包括一年一遇,百年一遇,千年一遇,分别对应平台的操作工况,极限工况和生存工况。
模型试验所需的大量波浪都在试验前进行了无流状态下的标定。对于随机的波浪现象,校准的参数以下:有义波高Hs,谱峰周期Tp,波谱密度曲线,最大波高,最大波峰高度。

表3 试验中用到的环境条件
风的模拟是通过对平台施加风载荷时历曲线实现的,并没有采用风扇阵列造风,而是通过电脑控制的动态伺服绞车直接施加风载。风力的时间曲线和对应的风谱都在试验前进行了校准。流载荷是通过施加重块实现的。力的作用点等效考虑了流载荷对船体,张力腿筋腱以及TTR的作用。
1.4 气隙波高仪的设置
为了在波浪试验中得到准确的气隙结果,试验中设置了22个气隙波高仪。波高仪的布置位置经过了仔细考虑以能综合评估试验的气隙结果。图3显示了斜浪时波高仪的布置情况。

图3 斜浪气隙波高仪布置图(红点代表波高仪)
2 试验结果和对比
试验过程进行了大量的工况并对其进行了深入的研究,限于篇幅,本文只列出了千年一遇斜浪工况的部分关键参数结果。模型试验的结果和数值结果进行了对比。在耦合分析中,通过非线性的时域丰度进行了动力分析,求解了整个系统的完整方程,同时考虑了浮体的刚体运动以及柔性杆件(立管和张力腿筋腱)。每个时间步都满足了动态平衡,保证了浮体和柔性体的耦合效果。
2.1 自由衰减试验
图4~图6显示了典型的纵荡、升沉和横摇的衰减试验结果。每个自由度的衰减试验都进行2次,对升沉和横摇,2次试验的初始位移是一致的;但是对纵荡,两次的初始位移分别是5 m和10 m。表4列出了固有周期和系统阻尼占临界阻尼的百分比。可以看出,模型试验的周期结果和数值预报的结果吻合良好。对于系统阻尼,纵荡和横荡的阻尼出现了一些差别,试验中增加的阻尼来自于结构附属物的流体力学阻尼及张力腿筋腱立管等的结构阻尼。

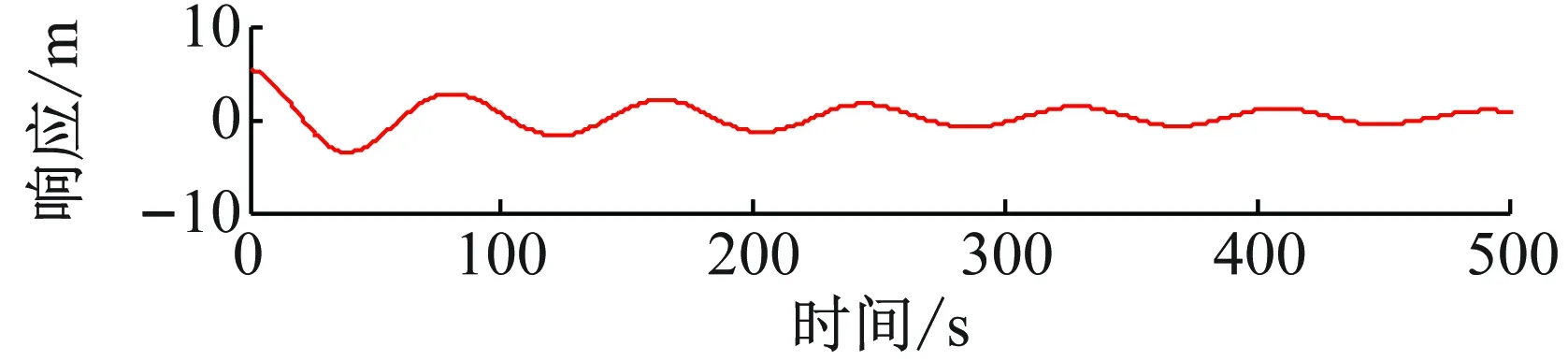

图4 纵荡自由衰减试验


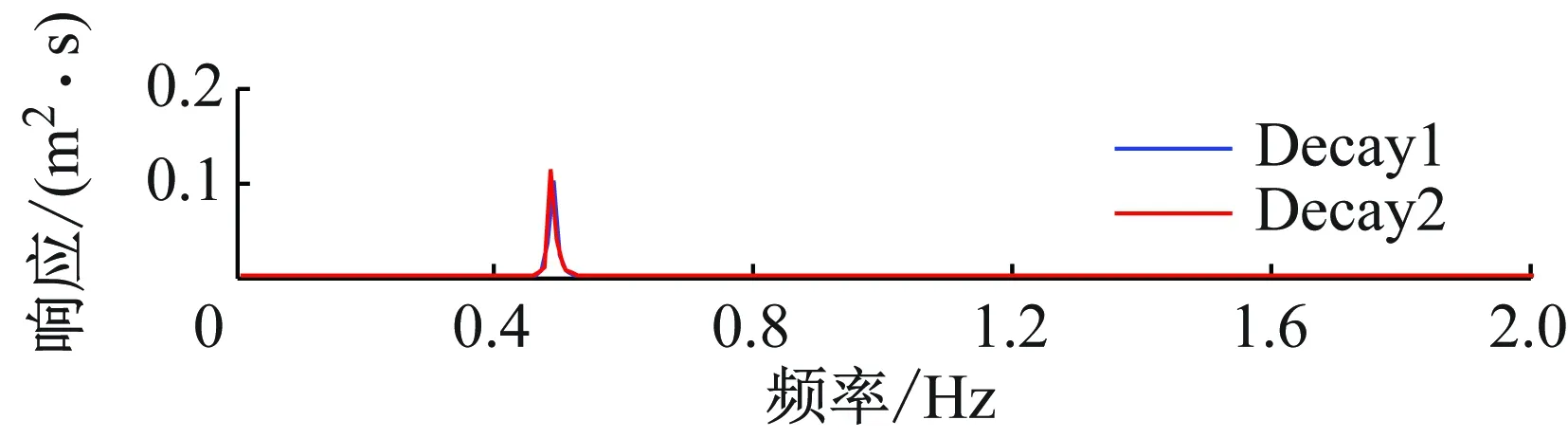
图5 升沉自由衰减试验
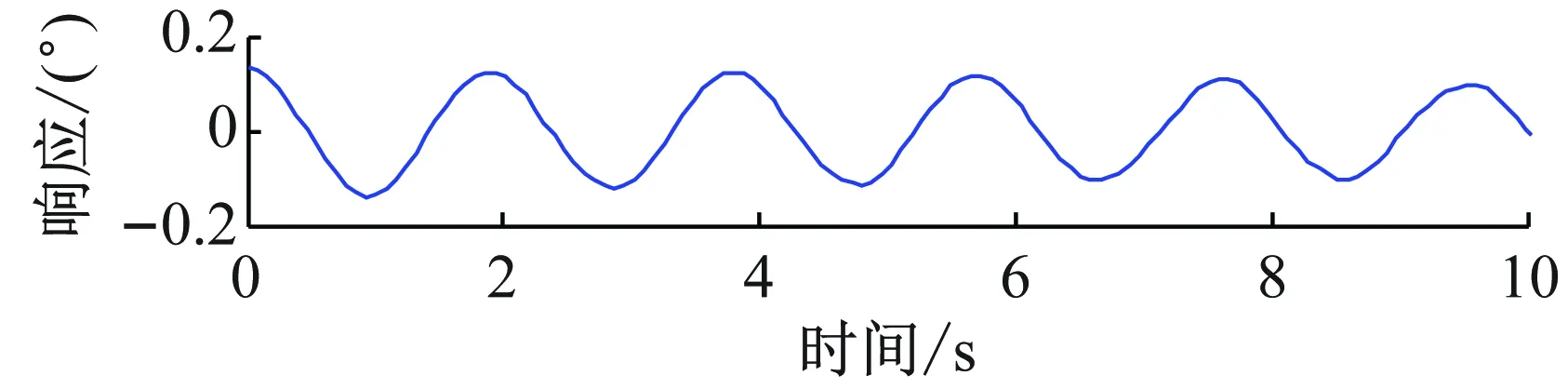


图6 横摇自由衰减试验
2.2 极限工况位移结果
图7显示了TLP平台的位移对比结果,A602-R1~R6代表千年一遇海况的6个种子的结果,包含数值分析得到的预报值和模型试验的导出值。可以看出,两者最大位移的结果相当接近,差别小于5%。

表4 固有周期和临界阻尼的百分比

图7 千年一遇海况最大位移
2.3 筋腱张力
图8和图9显示了千年一遇海况下迎浪处张力腿筋腱的张力。可以看出,平均值和极值都相当接近。数值分析的波频标准差(STD)有所高估,而高频标准差有所低估,这可能是由于张力腿筋腱在恶劣海况下的高阶响应造成的。

图8 千年一遇最大迎浪筋腱张力
2.4 气隙和上浪
研究多立柱式平台的上浪气隙响应是最近的研究热点之一,这对于油气开发的安全操作而言非常重要。气隙A(t)的定义如下:
A(t)=S-[η(t)-σ(t)]
R(t)=η(t)-σ(t)
σ(t)=ξ3(t)+yξ4(t)-xξ5(t)
其中:S代表甲板底部和平均海平面之间的初始静间隙;η(t)代表波面高度;σ(t)代表甲板指定参考点垂向运动;R(t)代表相对于甲板参考点的波面高度;ξ3(t),ξ4(t),ξ5(t)分别为甲板的升沉、横摇和纵摇运动。
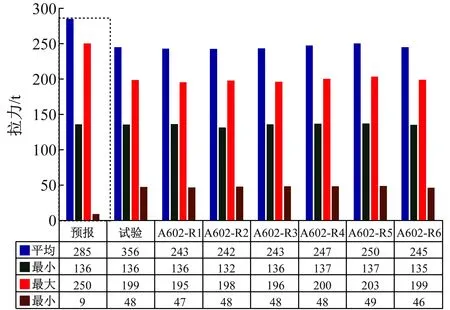
图9 千年一遇最大筋腱张力标准差
图10显示了一个极值气隙出现时的模型试验截图,最恶劣的情况发生在背浪处的立柱前沿。由图11可以看出,数值分析的气隙结果可能是低估的。这主要是由于立柱附近的波浪爬升是强非线性的,很难被数值模拟准确捕捉。同样可以看出,不同种子数下的模型试验气隙结果有明显差异(超过2 m)。因此建议,如果气隙是工程关心的参数,则应该进行足够多的种子数以便准确捕捉试验结果的差异。

图10 负气隙截图

图11 21号气隙波高仪处的相对波面高度(气隙)
2.5 张力腿筋腱弹振和鸣振
模型试验中,观察并记录了张力腿平台高频响应如弹振和鸣振现象。弹振是由于二阶和频激励在高频固有周期处产生的稳态响应,这种响应可以在商业软件中捕捉到,而鸣振是由于极限波浪的冲击载荷在高频固有周期附近产生的瞬间的自由振动。这种强非线性现象现有的计算流体力学应用尚存在理论难度,工程上多通过水池模型试验的方法解决。图12给出了千年一遇海况下迎浪筋腱的弹振和鸣振的响应幅度。
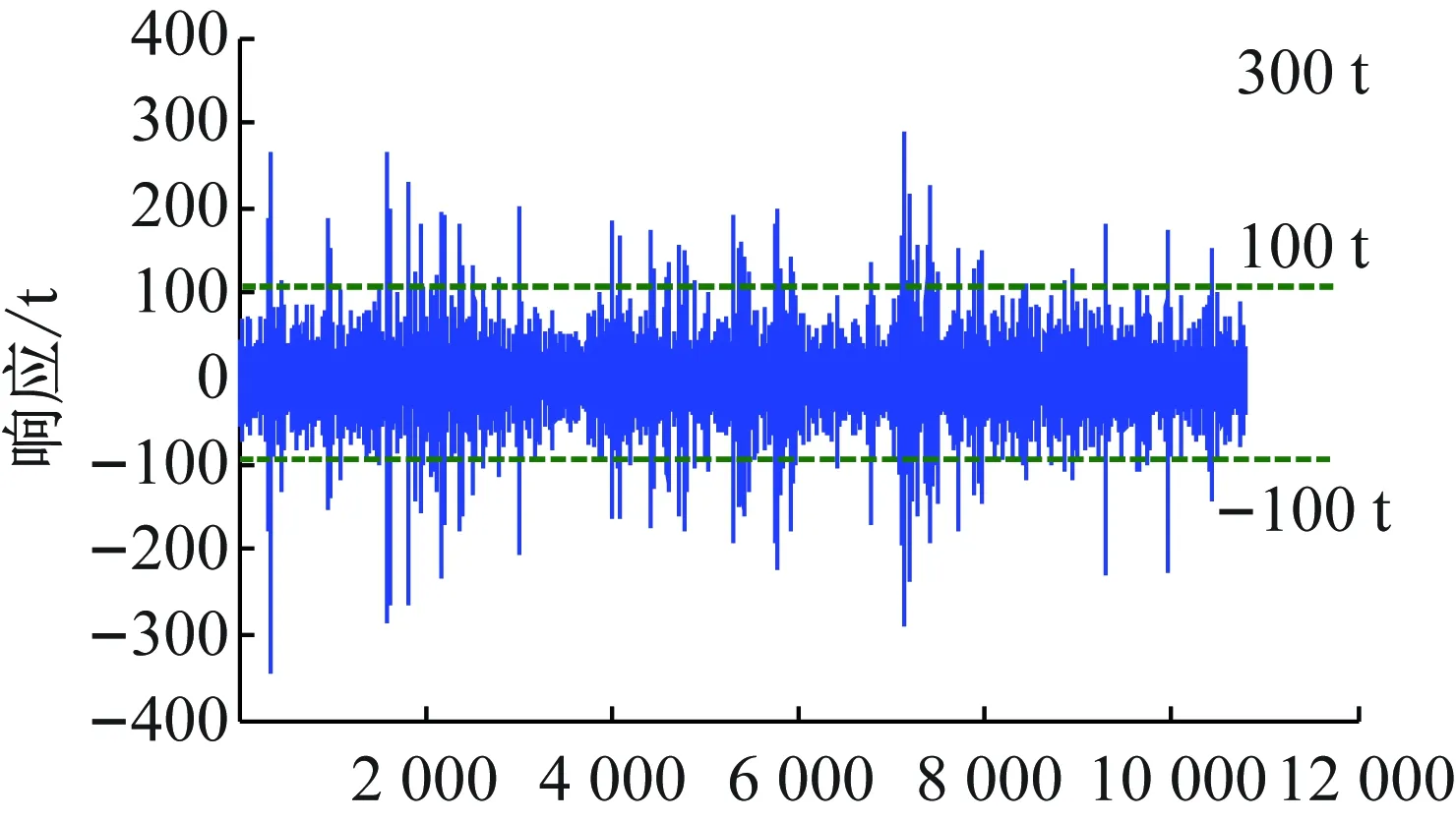
图12 千年一遇海况下筋腱弹振鸣振响应的幅度
3 试验数据修正
3.1 方 法
基于模型试验的测得结果,为了有效地指导工程实际,本文给出了工程上的修正方法。位移和张力的设计值通过下式进行校准:
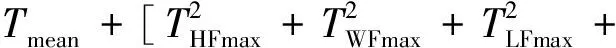
2α(THFmaxTWFmax+TWFmaxTLFmax+
THFmaxTLFmax)]1/2
(1)
(2)
(3)
(4)
式中:Tmax和Tmean代表设计参数的最大值和平均值;WFcorr,HFcorr,LFcorr分别代表模型试验和数值模拟模型试验结果间的波频,高频和低频标准差修正系数;α为波频,高频和低频最大值之间的耦合系数;脚标model和prediction分别表示数据来自于模型试验和数值模拟。
3.2 最大位移和筋腱张力
千年一遇工况的修正系数见表5,这些系数会应用到数值校准分析。
3.3 气 隙
同样应用上文提到的修正方法,气隙的千年一遇标准差修正系数和极值修正系数分别为1.059和5.067。这些系数会修正数值分析的结果,修正后的气隙等值线图见图13。最恶劣的气隙(-1.24 m)出现在背浪立柱的前沿,21号气隙波高仪位置处。这表示这个位置的局部结构可能需要加强。

表5 位移和筋腱张力的修正系数结果

图13 千年一遇斜浪下气隙等值线图
4 结 语
相对较浅的水深加之恶劣的环境对南海近海张力腿平台的设计应用提出了挑战。本文的模型试验结果可以为类似的工程提供很有意义的参考。
(1) 对于平台位移而言,主要由低频运动和波频响应构成,商业软件进行的耦合分析可以对此进行相当准确的预报;
(2) 在500 m水深以浅的TLP系统显示出了很强的非线性特质,特别是张力腿筋腱的高阶响应。试验中捕捉到明显弹振和鸣振现象;
(3) 气隙的测量也表明了响应的强非线性,恶劣海况下,可以清晰地观测到迎浪测立柱的波浪爬升现象;
(4) 本文对张力腿平台的强非线性响应数值预报提出了一种满足工程实际的修正方法,该方法综合考虑了高频、波频和低频修正,可供今后类似工程项目参考。
