基于改进PSO算法的嵌套环式微陀螺结构优化设计*
2018-12-10李青松侯占强吴学忠肖定邦
胡 倩,李青松,周 鑫,侯占强,许 一,吴学忠,肖定邦
(国防科技大学智能科学学院,长沙 410073)
嵌套环式MEMS振动陀螺近年来发展迅速,成为未来高性能微陀螺的一个重要方向。但目前关于嵌套环式MEMS振动陀螺的研究报道侧重于整体设计、精密修调[1]、信号处理等方面[2],针对嵌套环式结构本身的创新设计问题的研究鲜有报道。由于嵌套环式MEMS陀螺具备达到导航级精度的潜力,在工业产品和武器装备上具有非常重要的应用价值[3],而改变嵌套环陀螺的结构设计会引起陀螺性能发生很大的改变,因此研究并完善嵌套环陀螺结构的设计理论体系在提升陀螺性能方面具有很大的改进空间[4]。嵌套环陀螺由于结构复杂,参数众多,是典型的多参数模型,陀螺的结构设计对其性能的影响规律复杂,无法得到性能和参数的解析关系,因此需要采用优化算法对嵌套环式陀螺结构进行演化和优化[5-6],以提高嵌套环陀螺性能为目标,得到最优结构参数,并以此为依据合理地设计出一种新型的高性能嵌套环式陀螺结构。
近年来,粒子群优化算法(PSO)、蚁群算法、人工免疫系统、分布估计算法、协同进化算法、密母算法、文化进化算法等一些新的进化算法范例陆续被用于求解优化问题,而PSO算法由于流程简单易实现,算法参数简洁,无需复杂的调整,与其他算法易结合,从提出至今,已被迅速用于遗传算法原有的一些应用领域。PSO算法[7]是Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。本文将一种改进后的PSO算法引入到嵌套环结构参数优化设计中,通过目标函数与条件约束的设置,仿真计算其每一步的优化结果并得到最优结构设计,最终结果与未优化前进行对比并加以分析与验证。
1 嵌套环陀螺
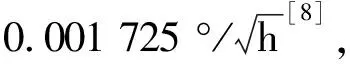
(1)
在对嵌套环陀螺进行结构参数变化时,单个变量可以直接进行仿真计算,但壁厚、间隙等多变量通过依次改变参数探索其变化规律对陀螺性能的影响操作复杂,仿真计算量过大,需要使用优化算法来进行嵌套环陀螺结构多参数的设计。本文主要以间隙分布优化作为研究目标,嵌套环陀螺的机械热噪声为优化目标,进行优化的嵌套环模型与波音设计的嵌套环模型具有相同的结构与环数,外径为8 mm[8],壁厚20 μm,厚度150 μm,锚点半径1.5 mm,具体结构如图1所示。
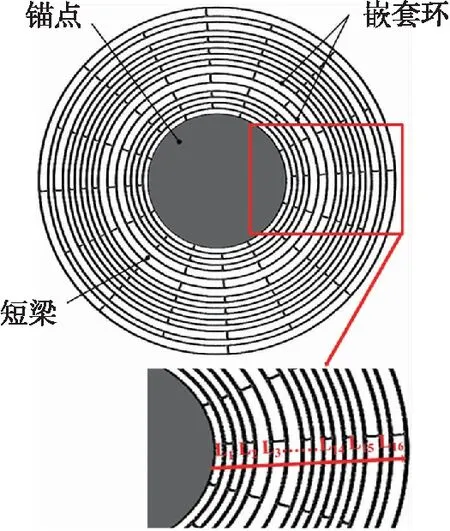
图1 嵌套环陀螺模型
2 优化算法流程
用来计算的PSO优化算法[9],可以在MATLAB中运行,也可以实现与Comsol等的对接[10]。将该PSO算法引入嵌套环的结构设计,优化算法主程序中的options结构体包含了所有需要修改和设定的选项,在主程序中可以设置嵌套环陀螺的外圆直径、环数、结构厚度、壁厚等结构参数,还可选择拓扑算法与领域范围,收敛精度等用于整个PSO的控制。
嵌套环结构优化时每个结构参数都可看作为一个独立的粒子,目标函数则为所期望提高进行优化的陀螺性能,例如特征频率、品质因子、机械灵敏度、机械热噪声等。程序中的state结构体用来存储在计算过程中的所有粒子的位置、速度、局部最优、全局最优等等所有值,并对其进行初始化。
建立的PSO优化算法[11]流程如下:
①state函数随机初始化粒子群体的位置和速度,本文的优化对象为嵌套环陀螺的间隙分布,因此每个粒子都是一种嵌套环陀螺间隙分布方式,间隙参数是在允许的范围内随机产生的。本文的粒子群体中设置了10个相互独立的粒子,将每个粒子的pbest坐标设置为其当前位置,优化的目标函数为嵌套环陀螺的机械热噪声,调用设置的目标函数计算出相应的个体极值(即该种间隙分布的最小机械热噪声),而全局极值(即全局最优值)是在比较粒子群体的个体极值中后(即粒子群体中的最小机械热噪声),记录最优值的粒子序号,即获得最小机械热噪声的间隙分布方式,并将gbest设置为该最优粒子的当前位置。
②更新粒子群的速度与位置:
(2)
(3)
种群数为m的粒子群落,其中第i个粒子的位置为xi,其飞行速度为vi,其中i=1,2,…,m。学习因子c1和c2为非负常数,用于控制粒子指向自身或邻域最佳位置的运动,通常取c1=c2=2。ω为惯性常数,控制粒子可能发生飞出问题空间,甚至趋向无穷大的现象。
③计算每个粒子的目标函数值,在本文中则是计算每种嵌套环间隙分布的机械热噪声,并与个体极值进行比较,如果较优,则更新当前的个体极值。
④对每个粒子将其目标函数值与全局极值进行比较,如果较优,则更新当前的全局极值。
⑤根据式(1)、式(2)再次更新每个粒子的位置和飞行速度,不断进行迭代。
⑥达到预先设定的停止准则(迭代收敛的精度或最大迭代次数),则停止计算,优化结束。粒子群优化算法流程图如图2所示。
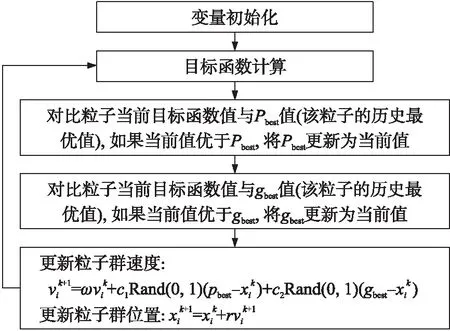
图2 PSO优化算法流程图
3 PSO优化算法改进
PSO算法在优化前期中收敛速度很快,但在优化后期中收敛速度变得缓慢,因而导致收敛精度低,这主要是粒子群难以摆脱局部极值的原因,会导致嵌套环陀螺在未达到最优解时便停止更新。对于嵌套环陀螺,其结构复杂,参数众多,由于间隙较多,不同的间隙变化会对陀螺整体尺寸产生较大的影响,且每个间隙都有一定的上下限,对于已经固定整体尺寸的嵌套环陀螺,需要对其间隙分布进行适当的条件约束,保证间隙总和是一个固定值,各个间隙在总和一定的情况下进行变化。针对这一系列问题,对PSO优化算法进行了算法改进。
3.1 引入极值扰动
优化过程中,粒子将聚集到由自身极值pbest和群体全局极值gbest决定的极值之上,如果所有粒子在向gbest靠近过程中没有找到优于gbest的位置,则进化过程将处于停滞状态,粒子逐渐聚集到gbest,粒子易陷入到局部极值中。调整自身极值和全局极值,使所有粒子飞向新的位置,这使所有粒子在迁移聚集新位置时会经历新的搜索路径和领域,因此发现更优解的概率较大[12]。基于此思想,本算法引入了极值扰动。采用进化停滞步数t作为触发条件,对个体极值pbest和全局极值gbest同时进行随机扰动。主程序设置达到T次优化无提升时就进行随机扰动。
(4)
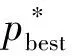
3.2 条件约束
在对嵌套环陀螺壁厚、间隙、环数等多变量参数进行优化时,为了保证嵌套环整体尺寸不变,变量总和往往为固定值,在总和一定的条件下,变量进行随机分布迭代优化,这样使得优化过程不仅复杂且变量不易控制。
本算法采用了随机固定求和函数randfixedsum来解决这一问题,该函数相当于求解n-1维单纯形(单纯形是最简单的拓扑凸集,例如1维单纯形是线段,2维是三角面,3维是四面体)内均匀取点的问题。通过狄利克雷分布将Rn上的n维均匀分布线性变换到n-1维单纯形上的均匀分布。使得程序产生一个n×m的随机矩阵,每一列是一个和为固定值s,各元素值满足条件限制a≤xi≤b的n×1列向量[x1;x2;…;xn]。
当主程序中设置好嵌套环陀螺的变量个数与每个变量的上下界,变量固定和,该函数就将产生一组随机变量,使得优化过程更加合理高效。针对嵌套环陀螺这种结构参数较复杂的对象控制程序也变得更加简洁易懂,方便操作。
4 实验验证与分析

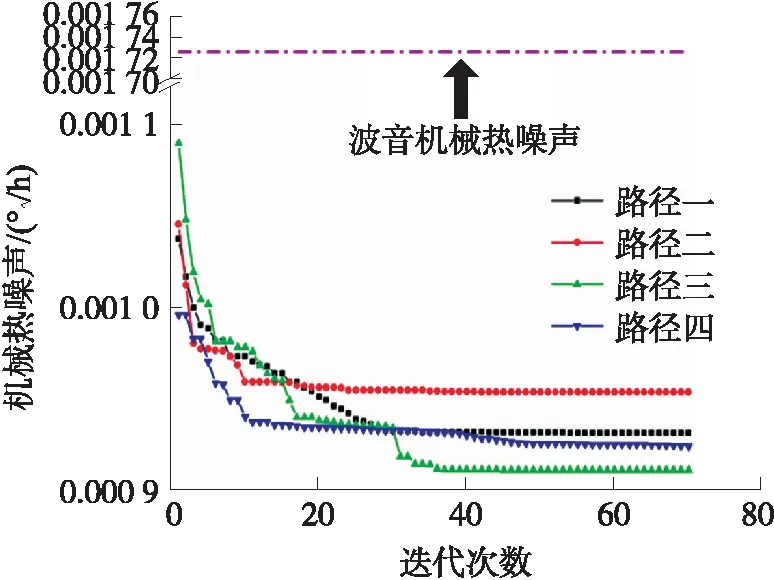
图3 嵌套环陀螺PSO间隙分布优化路径
同时由表1可以得出,经过算法进行间隙优化后的嵌套环陀螺频率与品质因子也有所提高。达到最优值的路径三相对于波音间隙非均匀分布嵌套环的频率增大了27%,品质因子提高了53%,优化后的陀螺在频率与品质因子两者之间有一个较好的均衡,整体性能有所提高,有效的提升陀螺的稳定性与灵敏度。

表1 优化前与优化后的嵌套环性能参数
由于4次不同的优化路径得到了4种不同的间隙分布,因此嵌套环陀螺的等效质量也随之发生改变,如式(5)所示,本文使用COMSOL with MATLAB得到嵌套环式谐振子的工作模态振型,提取模态1与模态2振型上所有节点的位移,通过节点平均的方法计算所有单元的位移。模态1、2所有单元在笛卡尔坐标系下的位移分量构成的矩阵[u1,v1,w1]、[u2,v2,w2]。其中q1和q2为模态1与模态2的波腹点位移最大值。保持外径,环数,锚点直径,壁厚,厚度一致,间隙进行优化后会导致嵌套环式谐振子的工作模态振型发生改变,从而等效质量也发生了改变。由式(1)可以看出,机械热噪声与陀螺的频率、品质因子、等效质量均成反比,通过间隙优化,嵌套环陀螺的频率、品质因子、等效质量相比于波音的陀螺均有所提高,在三者共同作用下陀螺的机械热噪声有了明显降低。
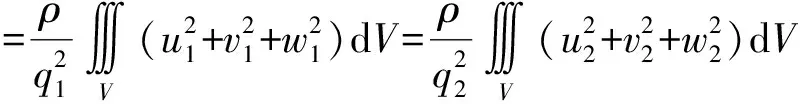
(5)
达到最优值的路径三的陀螺间隙优化过程如图4 所示,间隙编号从锚点处向外依次排序。优化过程最开始根据算法对16个间隙进行随机赋值,粒子开始进行迭代,慢慢根据目标函数朝最优值的间隙分布开始收敛,最终收敛到一个固定值。
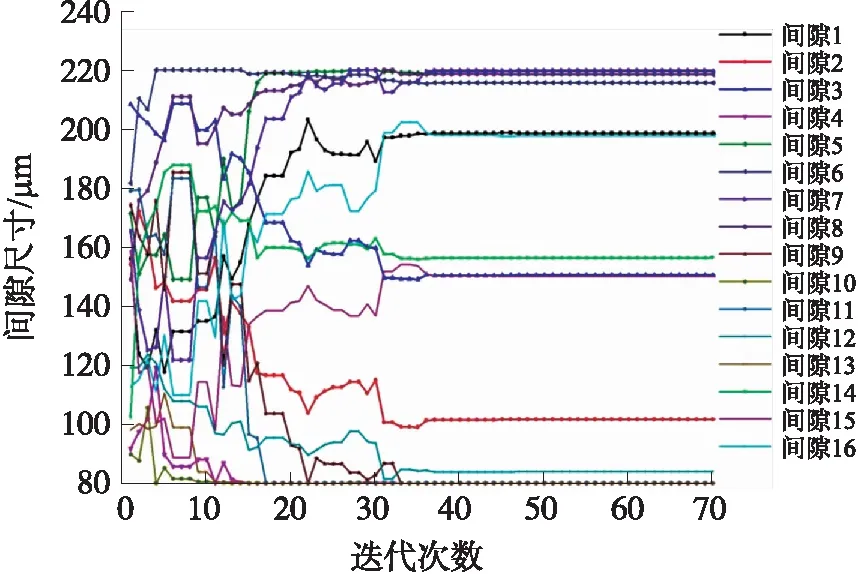
图4 路径三嵌套环陀螺间隙分布优化过程
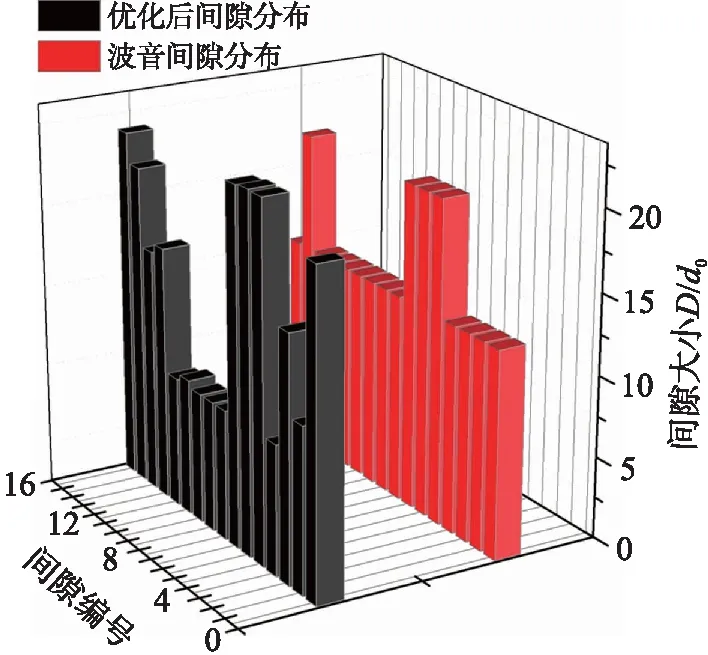
图5 嵌套环陀螺间隙分布图
从图4可以看到,间隙16、间隙5至间隙7的尺寸较大,达到了210 μm,间隙4、间隙8至间隙12尺寸较小,仅有80 μm左右,陀螺整体间隙分布如图5所示。由图5可以看出波音尺寸较大的间隙5至间隙7,间隙15在经过优化后同样具有较大的尺寸,而位于中间尺寸保持一致的间隙经过优化后尺寸仍大致保持一致,但较未优化前有所减小,同时在靠近陀螺锚点处与陀螺最外侧,间隙分布大致呈阶梯状变化。
5 结论
①本文提出的PSO优化算法有效的对嵌套环陀螺进行了间隙分布优化,成功提高了嵌套环陀螺的整体性能。
②加入极值扰动和条件约束的优化算法操作更加方便简洁,克服了PSO优化算法易陷入局部最优与嵌套环参数众多难以控制的问题,使结果快速收敛到全局最优值。
③利用PSO优化算法可以对嵌套环陀螺进行多变量参数的优化,研究陀螺结构设计对其性能的影响规律,对今后的嵌套环结构设计起一定的指导作用。
