汽轮发电机转子铁心电导率对失磁异步运行的影响

吴国栋，许国瑞，康锦萍，刘晓芳



汽轮发电机转子铁心电导率对失磁异步运行的影响

吴国栋，许国瑞，康锦萍，刘晓芳

（华北电力大学电气与电子工程学院，北京 102206）

由于汽轮发电机转子高速旋转，其转子通常采用整块实心钢构成。当发电机失磁异步运行时，转子铁心涡流产生的异步转矩对其动态运行具有重要影响，同时转子损耗及发热也会限制汽轮发电机的运行极限。为了研究转子铁心对汽轮发电机失磁异步运行的影响，本文采用时步有限元法计算了失磁异步运行过程中，不同转子铁心电导率下发电机转速的波动及损耗的大小，获得了不同转子铁心电导率下的损耗分布以及转子铁心典型位置的磁密变化。研究结果可为如何提高汽轮发电机异步运行能力提供理论依据。

汽轮发电机；实心钢；动态响应；损耗；激磁损耗；

0 前言

汽轮发电机失磁后能够工作在异步工况下并向电网供电[1,2]。短时异步运行能够有效避免供电中断、设备损害以及大面积停电，从而提高供电的可靠性。由于汽轮发电机转子高速旋转，转子材料通常采用整块实心钢制成。当发电机失磁异步运行时，转子铁心涡流产生的异步转矩对其动态运行具有重要影响，同时转子损耗及发热也会限制汽轮发电机的运行极限[4-6]。因此，研究转子铁心对汽轮发电机失磁异步运行十分有必要。

汽轮发电机失磁后需要从电网吸收无功功率来建立磁场[7-9]。转子铁心中产生的涡流可能会导致转子结构过热，将损坏转子绕组间的绝缘，继而引起转子绕组间的匝间短路。转子铁心中涡流的大小主要取决于铁心的电导率。对于汽轮发电机的失磁异步运行的研究通常基于发电机的电路模型[10,11]，但是电路模型参数难以反映转子铁心材料和集肤效应的影响[12,13]。

为了研究转子铁心电导率对汽轮发电机失磁异步运行的影响，本文选用了一台300MW、20kV、2极、50Hz的汽轮发电机作为研究对象，建立了汽轮发电机失磁异步运行的时步有限元分析模型。该模型可以考虑非线性因素，包括涡流的集肤效应、磁饱和以及交叉磁化对动态过程的影响[14-17]。为了分析转子不同铁心电导率对发电机失磁异步运行的影响，分别对铁心电导率在实际值附近变化±50%时的转速波动和转子损耗进行研究，揭示了发电机异步运行特性随转子铁心电导率的变化规律。

1 用于分析汽轮发电机失磁异步运行的场-路耦合时步有限元模型

1.1 时步有限元模型

根据麦克斯韦方程，汽轮发电机的电磁方程可以表示为：

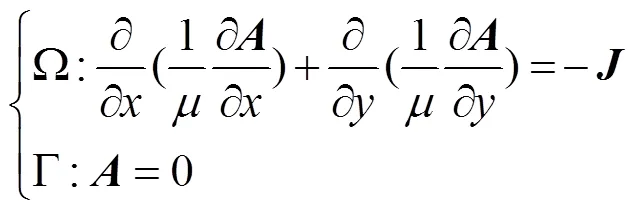
式中，是磁矢量；是磁导率；是电流密度。

定子绕组的电流密度st和励磁绕组的电流密度f可分别表示为：

式中，S，f分别为励磁绕组的匝数；S，f分别为定子和励磁线圈的截面积；s和f分别为定子电流和励磁电流；为定子的并联绕组数；“+”、“－”表示电流的方向。

转子铁心的涡流密度r表示为：

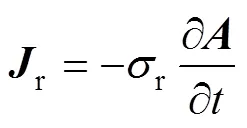
式中，r为转子铁心的电导率。

根据有限元离散和加权余量法，结合等式（1）~（3），可以得到：

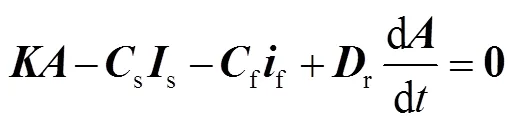
式中，为刚度矩阵；C，C为定子电流和励磁电流的关联矩阵；D为反映涡流的关联矩阵。

式（4）中的定子电流和励磁电流可通过式（5）得到：

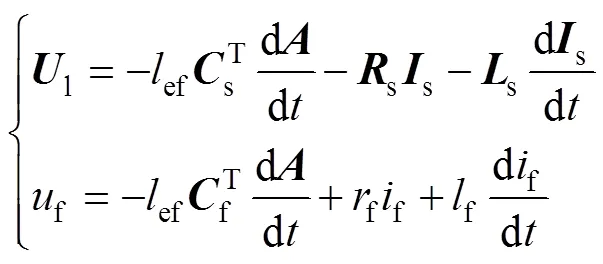
式中，=[A,B,C]T，s=[A,B,C]T，s=diag[s,s,s]，s=diag[s,s,s]，s和s为定子绕组的阻值和端部漏电感，f和f为励磁绕组的阻值和端部漏电感。

结合式（4）~（5）可以得到磁-路耦合的时步有限元模型如下：

1.2 反映转子涡流集肤效应的有限元离散策略

集肤效应会导致动态过程中转子铁心涡流分布不均匀。为了充分考虑集肤效应的影响，本文在计算过程中对转子表面进行了高密度有限元剖分，得到的转子铁心的剖分结果如图1所示，其中r和t分别为径向和切线方向的离散层数。图2为动态过程当中转子铁心的涡流密度。由图2可以看出，涡流密度随转子铁心的径向深度的增加而减小。同时，转子铁心的集肤效应也会导致转子损耗的不均匀分布。

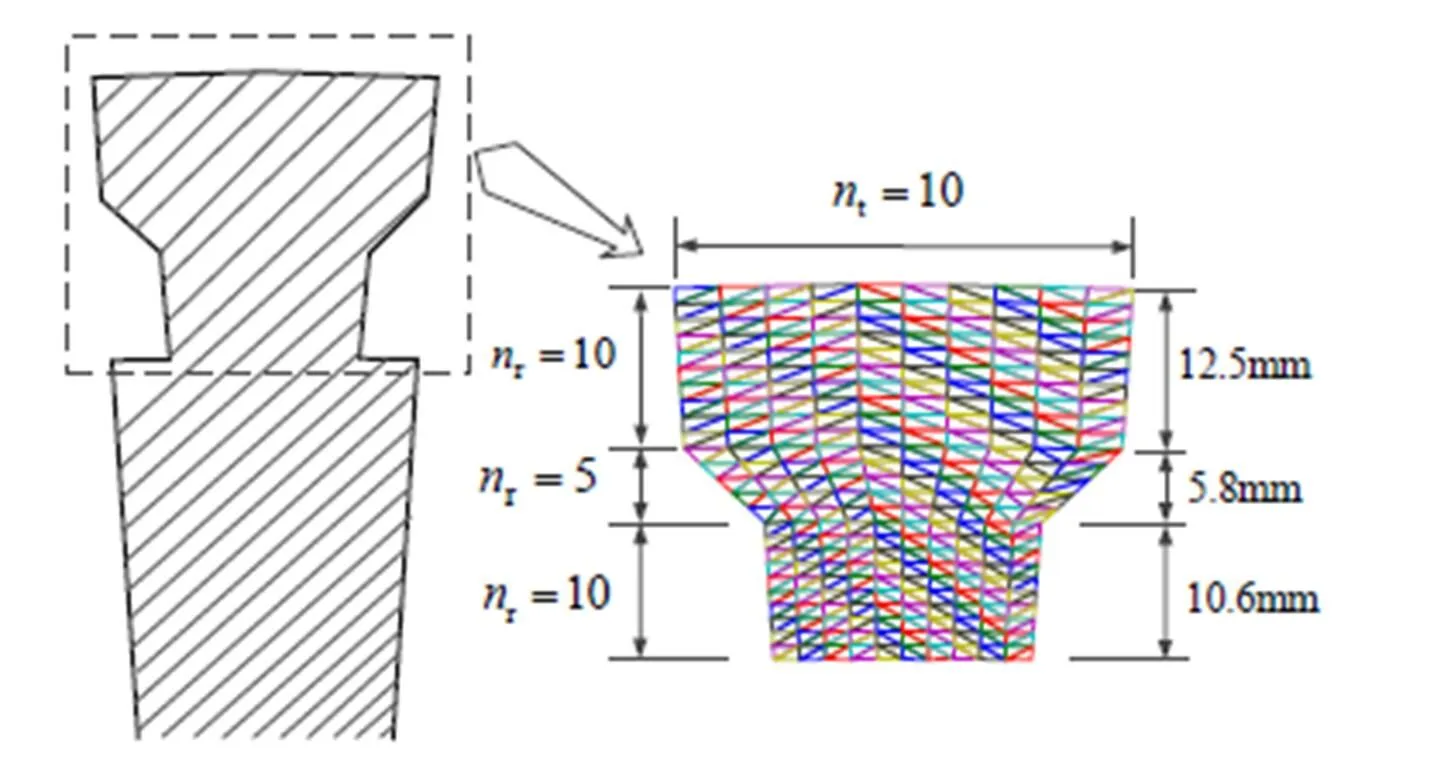
图1 转子铁心的有限元剖分网格

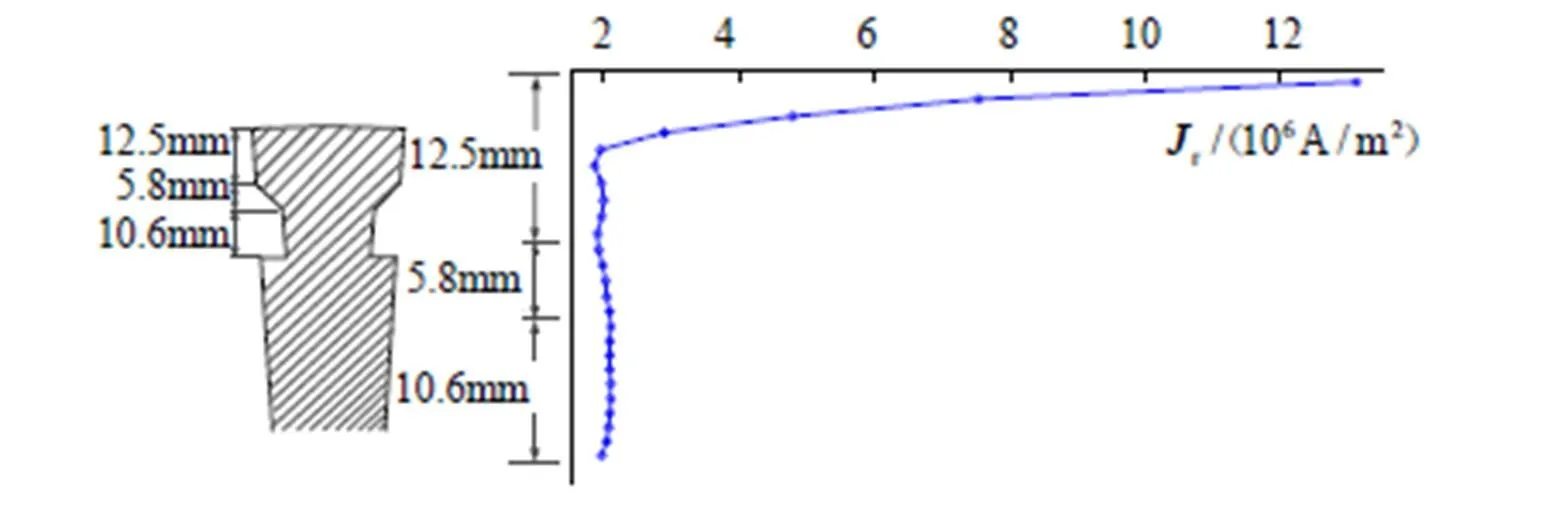
图2 动态过程中转子铁心的涡流密度

1.3 失磁异步过程中的转子铁耗的计算方法

汽轮发电机失磁后进入稳态异步运行阶段，转子转速会超过同步转速，并与同步转速之间存在一定的转差率。此时，汽轮发电机的转子损耗会明显增加，且主要为铁耗。转子铁耗的大小与铁心材料及转差率有关。基于时步有限元法，可以得到转子铁心中每个剖分单元的铁耗，如式（7）所示：

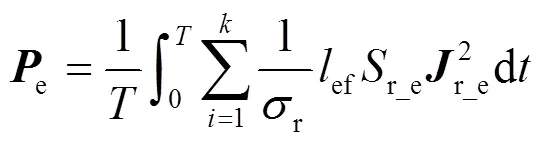
式中，P为转子铁耗；S_r为转子铁心的剖分单元面积；_e为转子铁心剖分单元的涡流密度；为周期。

1.4 模型机的实验验证

本文采用一台7.5kW模型机来验证所建立的时步有限元模型的准确性和有效性。7.5kW模型机的基本参数见表1，其二维截面图及模型机示意图如图3所示。

表1 7.5kW模型机参数

本文在7.5kW模型机上进行了空载三相突然短路实验，并将实验结果与时步有限元模型的计算结果进行了比较。图4所示为定子电流与励磁电流的对比结果，由图4可以看出，仿真结果与实验结果非常吻合。

图4 时步有限元仿真结果与7.5kW模型机实验结果对比

2 转子铁心电导率对汽轮发电机异步运行的影响

2.1 汽轮发电机失磁异步运行的分析方法

本文采用图5所示的系统仿真模型来研究转子铁心电导率对汽轮发电机的失磁异步运行的影响。发电机通过一台升压变压器和双回线路连接到无穷大电网。发电机的参数见表2。

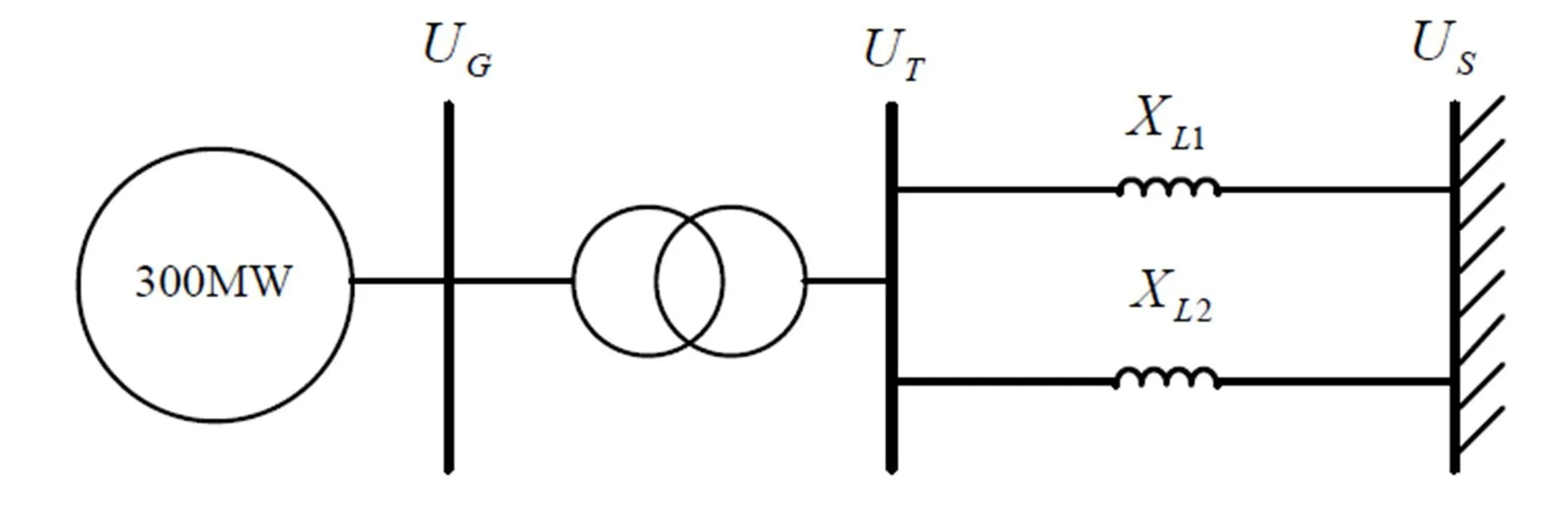
图5 仿真系统的示意图

系统扰动前的稳态运行工况通过给定的发电机励磁电压、系统功角以及电网电压来确定，其中励磁电压和无穷大电网的电压为定值，而系统功角可以在一定的范围内变化。汽轮发电机失磁后，励磁回路通过一个阻值为4.5倍励磁电阻的保护电阻形成闭合回路。

表2 汽轮发电机参数

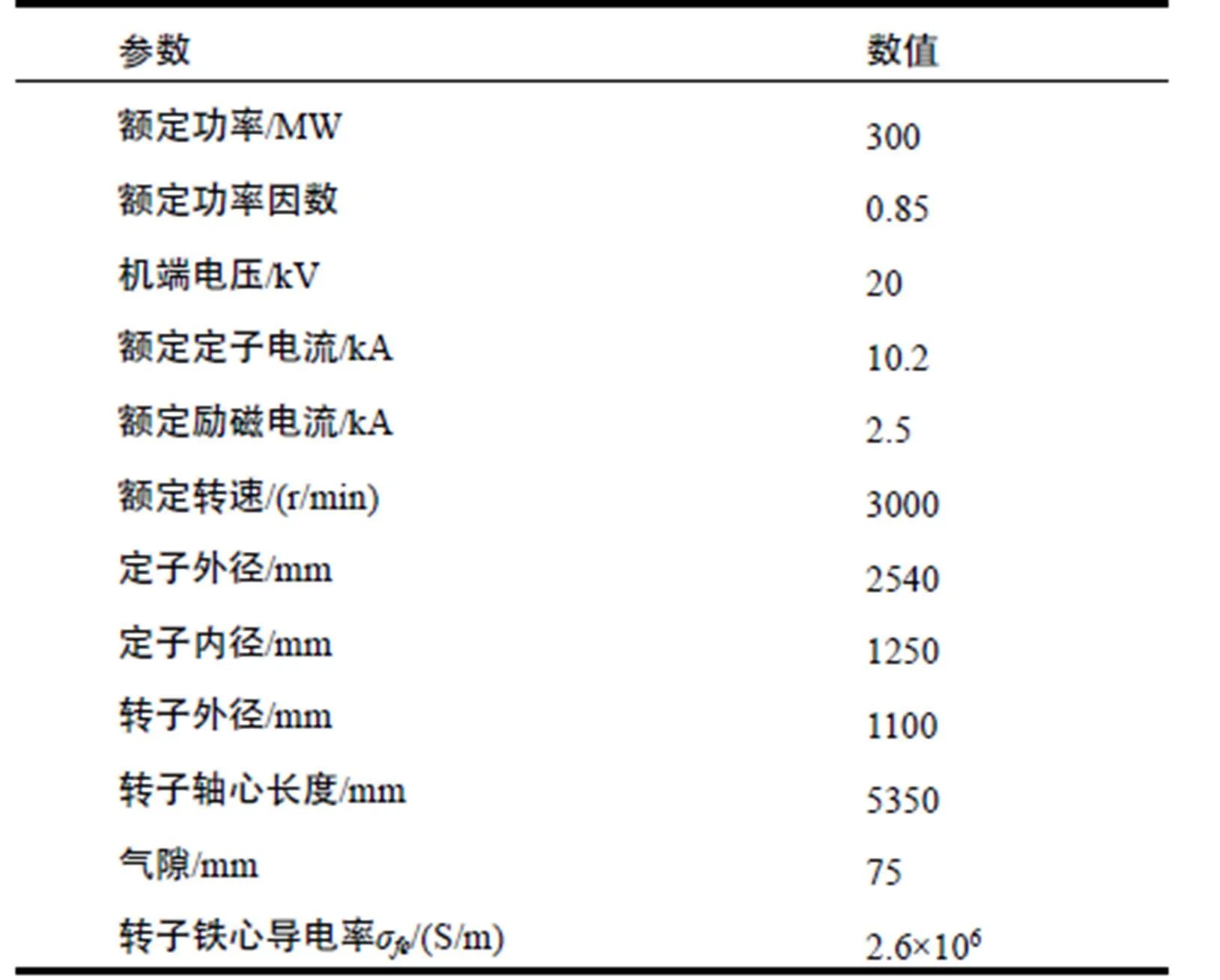
转子铁心不仅是发电机磁路的一部分，而且由于其导电性，转子铁心可在发电机失磁异步运行过程中提供阻尼转矩（异步转矩）。考虑到实心钢材料的多样性，本文对汽轮发电机铁心的电导率做如下三种情况的假设。

情况1：转子铁心电导率为σ的50%。

情况2：转子铁心电导率为σ。

情况3：转子铁心电导率为σ的150%。

2.2 转子铁心电导率对转矩波动的影响

汽轮发电机失磁之后通常要经历同步振荡、暂态异步运行以及稳态异步运行等3个阶段。由于其转子绕组不对称性，电磁转矩和转子转速在稳态异步运行过程中会出现明显波动。图6给出了三种情况下汽轮发电机失磁异步运行过程中的转子转速和电磁转矩变化曲线。从图中可以看出，三种情况下的转子转速和电磁转矩存在明显差别。

图6 三种情况下汽轮发电机失磁运行的动态响应

为了定量分析上述三种情况下的转速和转矩波动，本文设定了一些特性指标来对比分析汽轮发电机稳态异步运行过程中的特性，如最大电磁转矩max、电磁转矩波动flu、最大转速max以及转速波动flu，计算结果见表3。以情况2的计算结果作为参考，情况1中的电磁转矩波动flu是情况2的3.9倍；情况3的电磁转矩波动flu约为情况2的33%。情况1中转速波动flu是情况2的2.6倍；情况3中的转速波动flu约为情况2的50%。

表3 三种情况下的汽轮发电机特性指标

汽轮发电机稳态异步运行过程中的电磁转矩波动与转子绕组的不对称结构有关。发电机失磁后，励磁绕组经保护电阻短路，也会感应电流并产生异步转矩。励磁绕组的轴线与d轴重合，其产生的磁场主要作用在d轴，而转子铁心在d、q轴上的对称性明显优于励磁绕组，因此随着转子铁心电导率的增加，电磁转矩波动逐渐变小。

2.3 转子铁心电导率对铁耗的影响

通过改变转子铁心电导率，计算所得三种情况下的转子铁心平均损耗见表4。从表4可以看出，三种情况下转子铁心的铁耗相差较大，虽然转子铁心涡流的大小随着电导率越大逐渐增大，但是随着转子铁心电导率的增加，转子铁心损耗却逐渐减小。

表4 三种情况下的平均转子铁耗

为了获得发电机失磁异步运行过程中转子损耗和发热最严重的位置，计算并对比了三种情况下的汽轮发电机转子损耗的分布情况，结果如图7所示。从图7中可以看出，转子铁心损耗随着电导率的增加而减小，转子铁耗主要位于磁轭和磁极的表面。

2.4 失磁异步运行时转子铁心典型位置的磁密

发电机失磁将导致转子铁心的涡流增加，并且容易引起转子铁心部分过热和应力集中，因此对转子铁心中的磁场分布进行重点研究很有必要。通过计算上述三种情况下的汽轮发电机失磁异步运行过程，对比分析三种情况下转子铁心的磁场分布。为了便于分析，选取如图8所示的六个典型位置（A-F）来研究汽轮发电机失磁异步运行过程中不同铁心电导率对转子铁心磁密的影响。

图8 300MW汽轮发电机的二维纵切面

通过对比三种情况下转子大齿和小齿上六个点（A-F）处的磁通密度，得到如下结论：

（1）A点到C点的径向磁通密度的幅值小于切向磁通密度的幅值；A点的径向磁通密度接近正弦波；B点和C点的径向磁通密度畸变严重，谐波含量随着转子铁心电导率的增加而减小；

（2）D点到F点的径向通量密度幅值大于切向通量密度的幅值。随着转子铁心电导率的增加，D点到F点的切向磁通密度幅值逐渐减小。而径向磁通密度随转子铁心电导率的变化规律相同。D点到F点的磁场畸变程度减小；

（3）随着转子铁心电导率的增加，转子上六个点磁通密度的频率明显下降。

图9 发电机失磁运行不同转子位置的磁通密度

3 结论

当汽轮发电机失磁异步运行时，转子中的感应电流不仅会产生维持汽轮发电机正常运行的异步转矩，也会产生损耗及发热限制发电机的运行极限，因此选择合适的转子材料至关重要。本文以一台300MW的汽轮发电机为例，研究了转子铁心不同电导率对失磁运行过程中的转矩波动及损耗进行研究，得出如下结论：

（1）在失磁异步运行过程中，转子转速和转矩波动随着转子铁心电导率的增加而减小。分析得出电磁转矩波动与转子绕组结构的不对称性有关，转子铁心的对称程度明显优于磁场绕组，因此随着转子铁心电导率的增加，转子铁心作用增强，电磁转矩波动变小；

（2）随着转子铁心电导率的增加，转子铁心损耗逐渐减小。转子铁耗主要集中在转子的磁轭和磁极的表面；

（3）异步运行过程中，转子大齿处的径向磁通密度接近正弦波；而转子大齿中部和根部的磁密则会发生严重畸变。

[1] T. Amraee. Loss-of-field detection in synchronous generators using decision tree technique[J]. IET Gener. Trans. Distrib., 2013, 7(9): 943-954.

[2] Chien-Hsing Lee, Ling-Shen Ma, Ching-Hsiang Weng, Bin-Kwie Chen. Lessons Learned From the Generator Loss of Field at a Cogeneration Thermal Power Plant in Taiwan[J]. IEEE Trans. on Power Syst., 2011, 26(4): 2093-2100.

[3] D. Hiramatsu, T. Tokumasu, M. Fujita. A study on Rotor Surface Losses in Small to Medium Cylindrical Synchronous Machine[J]. IEEE Trans. on Energy Convers.,2012, 27(4): 813-821.

[4] D. Hiramatsu, T. Tokumasu, M. Fujita. A study on Rotor Surface Losses in Small to Medium Cylindrical Synchronous Machine[J]. IEEE Trans. on Energy Convers., 2012, 27(4): 813-821.

[5] Li Weili, Wang Purui, Li Yong, Xue Yi, Li Dong, Zhang Xiaochen, Zeng Jianjun. Influence of Rotor Structure on Field Current and Rotor Electromagnetic Field of Turbine Generator Under Out-of-Phase Synchronization[J]. IEEE Trans. on Mag., 2017, 53(6): 1-4.

[6] Feiyang Huo, Weili Li, Likun Wang, Yihuang Zhang, Chunwei Guan, and Yong Li. Numerical Calculation and Analysis of Three-Dimensional Transient Electromagnetic Field in the End Region of Large Water–Hydrogen–Hydrogen Cooled Turbo- generator[J]. IEEE Trans. on industrial electronics, 2014, 61(1): 13-16.

[7] M. Abedini, M. Sanaye-Pasand, M. Davarpanah, R. Iravani. A Loss-of-Field Detection Relay Based on Rotor Signals Estimation[J]. IEEE Trans. on Power Del., 2018, 33(2): 779-788.

[8] Hasani, Abbas, and F. Haghjoo. A Secure and Setting-Free Technique to Detect Loss of Field in Synchronous Generators[J]. IEEE Trans. on Energy Conver., 2017, 32(4): 1512-1521.

[9] E. Ajuelo, R. Gokaraju, and M. S. Sachdev. Identification of generator loss-of-excitation from power-swing conditions using a fast pattern classi-fication method[J]. IET Gener. Trans. Distrib., 2013, 7(1): 24-36.

[10] I M Canay. Determination of the model parameters of machines from the reactance operators xd(p), xq(p) (evaluation of standstill frequency response test)[J]. IEEE Trans. on Energy Convers., 1993, 8(2): 272-279.

[11] I. M. Canay. Advance Calculation of the Characteristic Quantities of Synchronous Machines and Comparison with measured values[J]. IEE Proc. Electric Power Appl., 1994, 141(1): 13-18.

[12] 郭可忠，赵军．汽轮发电机失磁异步运行数学模型的比较[J]．电网技术，1999，23(8)：13-16．

[13] Xu Guorui, Liu Xiaofang, Kang Jinping, Luo Yingli, Luo Wei. The influence of turbine generator rotor damping structure and material on first swing stability[J]. Electric Power Systems Research, 2015, 124(1): 181-189.

[14] Hamed Hamzehbahmani, Philip Anderson, Jeremy Hall, David Fox. Eddy Current Loss Estimation of Edge Burr-Affected Magnetic Laminations Based on Equivalent Electrical Network-Part I: Fundamental Concepts and FEM Modeling[J]. IEEE Trans. on Power Del., 2015, 29(2): 642-650.

[15] L Xiaodong, A. M. El-Serafi, S. O. Faried. Application of the Finite Element Method for the Determination of the parameters representing the cross magnetizing in saturated synchronous machines[J]. IEEE Trans. on Energy Convers., 2010, 25(1): 71-79.

[16] 李伟力，孙佳慧，孙宏丽．汽轮发电机稳态与负序工况下转子涡流损耗计算和温度场分析[J]．电工技术学报，2012，27(9)：174-185．

[17] 康锦萍，刘晓芳，罗应立，等．汽轮发电机磁路饱和与磁场畸变共同作用对运行的影响[J]．中国电机工程学报，2010, 30(36)：41-45．

Influence of rotor core conductivity on the asynchronous operation of turbogenerator during loss of excitation

WU Guodong, XU Guorui, KANG Jinping, LIU Xiaofang

(School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

The rotor of turbogenerator is made of solid steel, for its high speed rotation. When the generator is in asynchronous operation, the asynchronous torque generated by the rotor core eddy current has an important impact on its dynamic operation, while the rotor loss and heat will also restrict the operating limit of the generator. In order to study the influence of the rotor core on the asynchronous operation of the turbogenerator, the time-stepping finite element method is used to calculate the fluctuation of the generator rotation speed and the loss of the generator under different rotor core conductivities. The loss distribution under different rotor core conductivity and the magnetic density variation of the typical position of the rotor core were obtained. The results provide theoretical basis for improving the asynchronous operating ability of turbogenerator.

turbo generator; solid steel; dynamic response; losses; loss of excitation

TM311

A

1000-3983(2018)06-0047-06

国家自然科学基金（51507059和51477049）中央高校基本科研业务费专项资金资助项目2018MS010

2018-02-22

吴国栋 (1992-)，就读于华北电力大学电气工程专业，硕士研究生，研究方向为电机与电器。