一道中考压轴题的多变思考与教学建议
——以“2013年湖南长沙中考数学卷的压轴题”为例
2018-12-07陈惠增
陈惠增
(福清市高山育才中学,福建 福州 350300)
中考压轴题是难度较大的综合题,重在考查学生分析问题和解决问题的综合能力,历年各省市的中考压轴题不但体现命题专家的智慧,而且通过试题为载体更能体现命题者对课标与教材的理解,作为一线的教师应该对试题深入剖析与思考,提出解决此类题目的教学建议,提升学生解题能力,培养学生的“四能”(即分析问题、解决问题、发现问题、提出问题)。下面是笔者对“2013年湖南长沙中考数学卷的压轴题”的多变思考,并谈一些教学建议,供同仁们参考。
一、原题的多变思考
1.原题的分析思考
“2013年湖南长沙中考数学卷的压轴题”(以下简称“原题”)如图1,在平面直角坐标系中,直线y=-x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.
(1)求∠OAB的度数
(2)求证:△AOF∽△BEO
(3)(略)
【略解】(1)因为直线 y=-x+2,所以 A(2,0),B(0,2),则 OA=OB=2.因此∠OAB=45°;
(2)因为四边形OMPN是矩形,
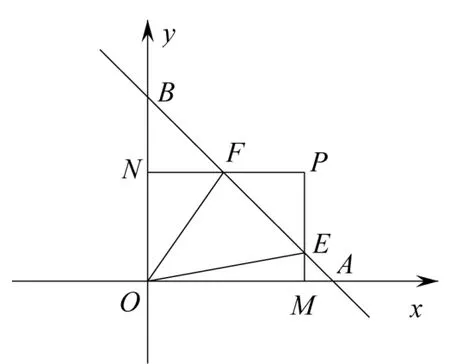
图1
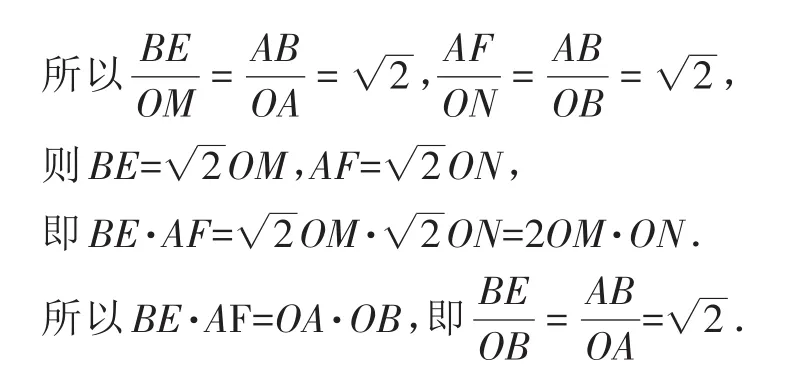
则△AOF∽△BEO;
【评析】(1)当x=0或y=0时分别可以求出y的值和x的值就可以求出OA与OB的值,从而就可以得出结论;对于直线y=kx+b与x轴、y轴的夹角问题与k的关系,特别指出当k=±1时,求直线y=kx+b与+x轴、y轴与夹角的度数。
2.原题的多问思考
多问1:求∠EOF的度数。
【略解】△AOF∽△BEO,则∠AOF=∠BEO,而∠AOF=∠EOF+∠AOE,∠BEO=∠OAB+∠AOE,所以 ∠EOF=∠OAB=45°。
【联想】北师版《义务教育教科书·数学》九年级上册P90的第4题(以下简称“联想题”):如图2,将两个全等的等腰直角三角形摆成如图所示的样子(图中的所有点、线都在同一平面内),请在图中找出两对相似而不全等的三角形,并说明它们相似的理由。
【评析】通过这两道题目的类比,可发现两题的图形结构特征相似,都能求证出△AOF∽△BEO,但证明三角形相似的方法不同,此道联想题是通过“两角分别相等”的方法证明三角形相似。
多问2:如图3,已经求得∠EOF=45°。求证:AE2+BF2=EF2。
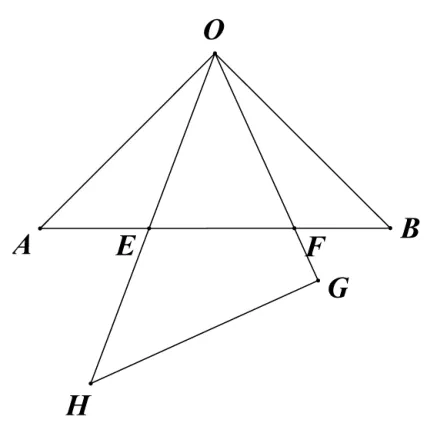
图2

图3
【略解】证法1:(旋转法)
如图4,把△OFB绕点O顺时针旋转90°,点F与F′对应,点B与点A重合,可证明△OF′E≌△OFE,在Rt△AEF′中,AE2+AF′2=EF′2,即 AE2+BF2=EF2成立。
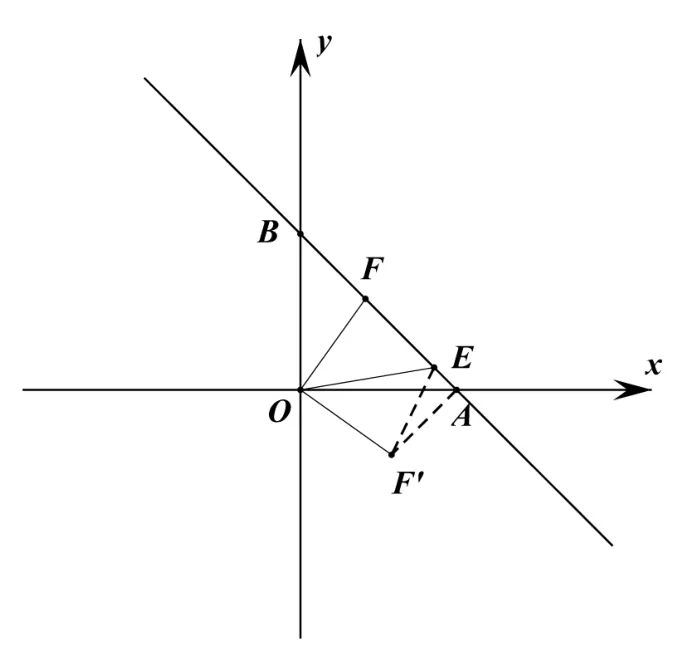
图4

图5
证法2:(折叠法)
如图5,把△OBF沿线段O F折叠,B点与B′对应,可证△OB′E≌△OAE,
在 Rt△EB′F 中,EB′2+FB′2=EF2,即 AE2+BF2=EF2成立。
证法3:(代数法)
由△AOF∽△BEO得OA·OB=AF·BE,
即OA2=AF·BE,所以AB2=2A F·BE,
因为 AB2=(AE+EF+BF)2=AE2+EF2+BF2+2AE·EF+2AF·BF+2EF·BF,2AF·BE=2(AE+EF)(BF+EF)=2AE·BF+2AE·EF+2EF·BF+2EF2。
即AE2+BF2=EF2成立。
证法4:(坐标法)
如图6,由P(a,b)及直线y=-x+2,可得A(2,0),E(a,2-a ),F(2-b,b),B(2,0),
由勾股定理可得:
EF2=PF2+PE2;即 EF2=2(a+b-2)2=2a2+2b2+4a b-4a-4b+8
BF2=BN2+NF2,即 BF2=2(2-b)2=2b2-8b+8
AE2=AM2+EM2,即AE2=2(2-a)2=2a2-8a+8
又ab=2,所以AE2+BF2=EF2成立。

图6
【评析】这三种证法中,前两种主要以几何思路为主,如何把在同一条线上的三条线段转化构造一个直角三角形而得证;第三种代数解法是从式子的左右两边出发,以代数计算为主证明等式两边相等;第四种以点坐标呈现,也转化成线段长,用勾股定理构造等式,通过计算得证,也应该是代数计算为主的证法。
3.原题与联想题的类比思考
对于“原题”多问得到:AE2+BF2=EF2;而对于“联想题”可继续进行变式。
追问1:如图7,分别过点E、F作PM⊥OA,PN⊥OB,垂足分别为点M、N,PM与PN相交于点P,设OA=OB=2,等腰直角三角形OHG摆动过程中(点E、F都在斜边AB上),矩形PMON的面积是否发生变化,若不变请求出矩形PMON的面积。
【略析】此题又回到“原题”,因此等腰直角三角形OHG摆动过程中(点E、F都在斜边AB上),矩形PMON的面积不会发生变化,S=ON·OM矩形PMON
追问2:如图7,分别过点E、F作PM⊥OA,PN⊥OB,垂足分别为点M、N,PM与PN相交于点P,等腰直角三角形OHG摆动过程中(点E、F都在斜边AB上),矩形PMON的面积不变,设OA=OB=2,矩形PMON的边长ON为y,边长OM为x,请求出y与x的函数关系式。
【评析】从上面原题与联想题的类比思考,可得到只要对题目进行适当的“张冠李戴”会有不一样的效果,因此解题教学要教会学生进行对比的“张冠李戴”。
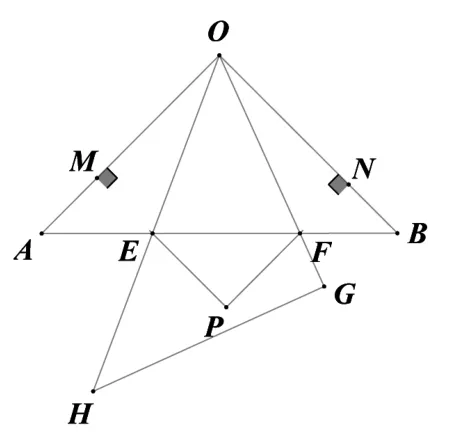
图7
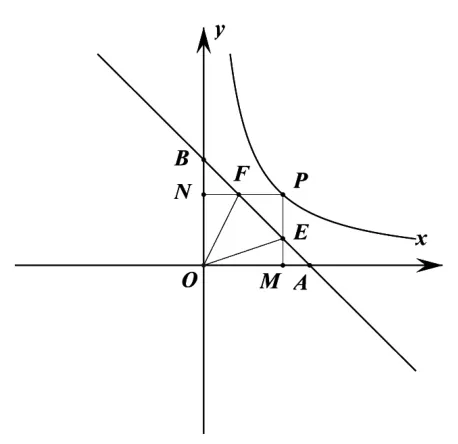
图8
4.原题的拓展思考
对原题适当的改变:如图8,在平面直角坐标系中,直线y=-x+2与x轴,y轴分别交于点A,点B,动点 P(a,b)在函数x>0)的图象上运动,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F。(1)求证:△AOF∽△BEO;(2)求∠EOF的度数。
拓展1:图形变化,如图8、如图9,其他条件都不变,(1)求证:△AOF∽△BEO;
(2)求∠EOF的度数。
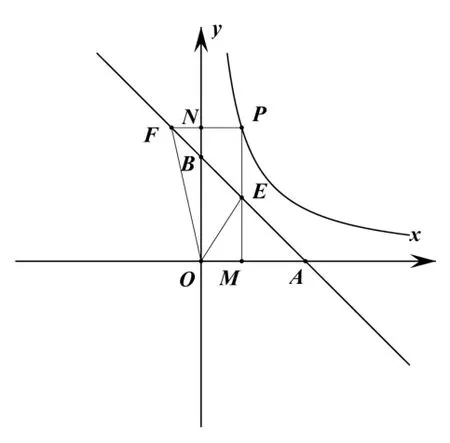
图9
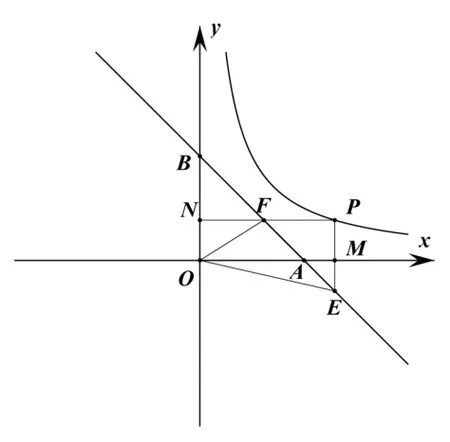
图10

图11
【评析】图9、图10都能用上面相同的方法求证△AOF∽△BEO,也能求得∠EOF=45°。虽然图1、与图2的证明方法与所求的结果都与原图的一样,但图形毕竟不同,教学中一定要让学生多见不同的图形,这样不但见多识广,而且能进一步固化解题方法。
拓展2:如图11,在平面直角坐标系中,直线y=-x+b与 x轴,y轴分别交于点A,点B,动点P(a,b)在函数0且k>0)的 图 象上运动,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F。若△AOF∽△BEO,求b与k的关系式。
【评析】△AOF∽△BEO,则 ,
即OA·OB=AF·BE。
从上述求的一般性的结论“b2=2k”,可回头进行特殊性的验证,如当“b=2,k=2”时,则回到原题,当然还可进行其他特殊性的推广,如当“b=3”时,要满足其他所有条件下,若要△AOF∽△BEO,则因此从原题到拓展2的是特殊到一般的思考,这种思考性的变化,在解题中进行尝试,会提升学生提出问题与发现问题的能力;而拓展2与原题的解题过程又是可逆的过程,常进行这方面的训练会培养学生的全面思维能力。
二、析题解题的教学建议
对于中考压轴题与其他课本大题解题析题的要求不一样,毕竟中考压轴题的综合性较强,因此对于中考压轴题的析题解题的教学到位,更会提升学生的“四能”。《义务教育数学课程标准(2011年版)》明确提出:数学教学应根据具体的教学内容,创设问题情境,引导学生通过实践、思考、探索、交流等,获得“四基”(即基础知识、基本技能、基本思想、基本活动经验),促使学生主动地、富有个性地学习,不断提高发现问题和提出问题、分析问题和解决问题的能力。
为了提高中考复习的效果,更为了提升学生的“四能”,对于中考压轴题的解题教学应该遵循“五步”的基本套路。
1.理解题目。理解题目可分为“熟悉题目”和“深入理解题目”两个阶段。首先,必须理解该题目的语言陈述,弄清这些题目的“未知量是什么?已知数据是什么?条件是什么?”之后再深入理解题目,理解这些未知量与已知量之间的关系,从各个方面来考虑题目的主要部分。
2.拟订方案。从理解题目到构思一个解题的方案也许是漫长而曲折的过程,解答一个题目的主要成就在于构思一个解题方案的思路,而这思路可能是逐渐形成的,教师能为学生所做的是引导学生获得一个好的思路,为此必须能够了解学生的状况,教师应该认真回顾自己在解答此题目时遇到的各种困难和取得的各种成功。好的思路还来源于过去的经验和以前获得的知识。如求证“原题”的第2问题△AOF∽△BEO时,结合图形联想到“联想题”的图形,通过这两道题目条件与图形的类比,多次尝试修改,从而拟定解决此题的方案。
3.执行方案。解题方案给出了一个总体框架,必须确认细节都符合这个框架,可以用“直觉的”或“形式的”证明确认每一步推理的正确性。如证明上述“原题”中△AOF∽△BEO时,从计算方法证BE·AF=OA·OB,再通过“两边成比例且夹角相等”证△AOF∽△BEO相似,这其中的每一步都得“言之有据”。
4.回顾思考。从执行方案得到解答,检查每一个步骤,尽管如此,错误总是有可能存在的,因此需要进行验证,而验证可以不同的方式进行。通过回顾思考让学生明白,数学题之间是相互联系的,并让学生意识到回顾思考是很有收获的。
5.反思总结。对于中考压轴题的解题教学,更应该让学生进行反思总结,应该从知识、方法、拓展三个方面进行总结。如以“原题”为例:(1)本题涉及知识。一次函数、矩形、平行线性质、勾股定理等;(2)本题涉及的方法。分析法与综合法、特殊与一般、数形结合;(3)本题拓展。从上述拓展可进行纵向的多问拓展,还可进行横向的类比拓展。
对“原题”的再分析与思考,不但培养学生“四能”,即分析问题、解决问题、发现问题、提出问题,还能对中考压轴题的解题教学提供一些教学建议。
