指向能力立意的高考数学复习策略

黄炳锋

（福州第三中学，福建 福州350003）

1999年2月，教育部在《关于进一步深化普通高等学校招生考试改革的意见》中指出：高考数学卷命题要“更加注重对考生能力和素质的考查”“在试题设计上增加应用型和能力型的题目”，“能力立意”的命题指导思想自此确立。近二十年过去了，这一指导思想在高考复习的实践中贯彻得如何呢？笔者观察发现，情况并不乐观。许多教师仍然采用“知识立意”命题指导思想的做法，缺乏“问题意识”和“能力目标”，花费大量时间用于知识点复习。为了提高复习效率，章建跃教授提出“能力立意，问题导向，基于测评，追本溯源，精准高效，大幅提分”的核心理念，并依托中国教师研修网、中国教研网开展“基于测评的高考数学复习改进研究”课题研究，多次举办“能力立意，基于测评”引领下的高考数学复习课例研究活动，探索“能力立意”的高考数学复习之法。

一、以梯度问题为线索规划内容

高考数学复习首先要解决“教什么和学什么”的问题。毫无疑问，教学内容的确定比“怎么教”更重要。而高考数学复习的现状是，教辅书承包了教学内容和逻辑顺序，有的教辅书甚至还提供了教学课件和相应的测试训练以及参考答案，教师在教学时不考虑教学内容选择的适当与否，缺乏对针对性、代表性问题的思考，也没有为能力提高而进行梯度设计，教学过程照本宣科，三轮复习的教学内容不断重复。

“能力立意，问题导向”的高考数学复习，首先要在研究近年高考试题的基础上，将高考数学考查的内容划分为若干板块，然后针对每一板块的高考试题以及相应的能力要求，采用“追本溯源”的方式，将它们按题型特征和考查特点分成若干个考查问题，并依据必备知识、关键能力、学科素养、核心价值等设计每个考查问题，最后根据考查问题规划数学复习教学内容，以通性通法为核心展开复习教学。数学复习时要抛弃“先学基础知识和基本技能，然后逐步组合，最后才能综合运用”的传统教学思维，不把板块知识内容拆解成零碎的知识点、公式和定理，而是要有问题意识，进行单元教学设计，通过具体的考查问题设计串联起必备知识，在问题解决中培养关键能力、渗透数学思想、提升核心素养。

每一板块的考查问题承载着三轮复习需要的具体能力要求，以及考查的数学思想方法和数学学科核心素养。为了达成这个目标，复习过程中需要分解考查问题的教学目标，将能力要求分层设计，以梯度问题为线索规划教学内容。先将高考数学考查问题划分为几个小问题，每个小问题突出解决考查问题的一个核心内容及综合运用的方法，成为第二轮复习重点攻克目标。每个小问题还可划分为若干个具体问题，每个具体问题就是第一轮复习要解决的主要知识点和关键能力。值得注意的是，三轮复习的轮次划分标准是能力的达成度，而不是时间节点或知识点多少，对于难度不大的板块，教师基于测评做出判断，可能出现直接带领学生进入第二轮或第三轮复习的情况，即跳过具体问题直接进入以小问题或考查问题作为复习对象进行教学。考查问题、小问题与具体问题的层次关系如下：（如下页图1）

例如三角板块，根据高考题型特征和考查特点，可以分成三个考查问题：1.利用正余弦定理、主要的三角公式、基本不等式等知识，通过转化与化归、函数与方程等思想，经过运算、推理，解三角形及有关问题。该考查问题在高考中主要以解答题形式出现。2：利用主要三角公式变形求值。该考查问题在高考中主要以小题形式出现。3：利用主要的三角公式变形，并根据三角函数的图象或性质分析有关三角函数的图象、性质或求值。该考查问题在高考中主要以小题形式出现。

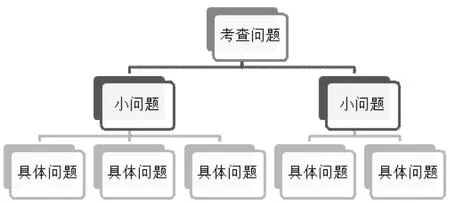
图1 考查问题、小问题与具体问题的层次关系

对于考查问题一，通过归纳发现此题主要考查解三角形和求与三角形有关量的问题。求解三角形有关量的问题的一般方法是把已知条件用三角形的边、角表示为等量关系，通过变形推理求得结果；求解三角形的一般方法是根据已知条件，利用正弦定理、余弦定理、主要三角公式等，将已知条件转化为关于三角形的边或角方程，求出边、角，进而求解。

依此可以设计三角板块考查问题一、小问题与具体问题的层次关系如下：（如图2）

图2 三角板块考查问题一、小问题与具体问题的层次关系

为了检测教学是否达成目标，还需对具体问题、小问题与考查问题三个层级目标进行具体划分（如表1）。达成目标层级一，即可进入第二轮复习，同样，达成目标层级二，即可进入第三轮复习，目标层级三是三轮复习最终要达成的能力目标。

针对不同目标层级要求，分别设计若干个用于教学的考查问题、小问题和具体问题，以及难度相当的能力测评与目标检测试题，示例如下。

考查问题：设△ABC内角A，B，C的对边分别为a，b，c，面积为S。已知2S=a2-abcosC。

（Ⅰ）求B；

（Ⅱ）若b=2，求S的最大值。

分析：这是一个求三角形有关量和面积最大值的考查问题。

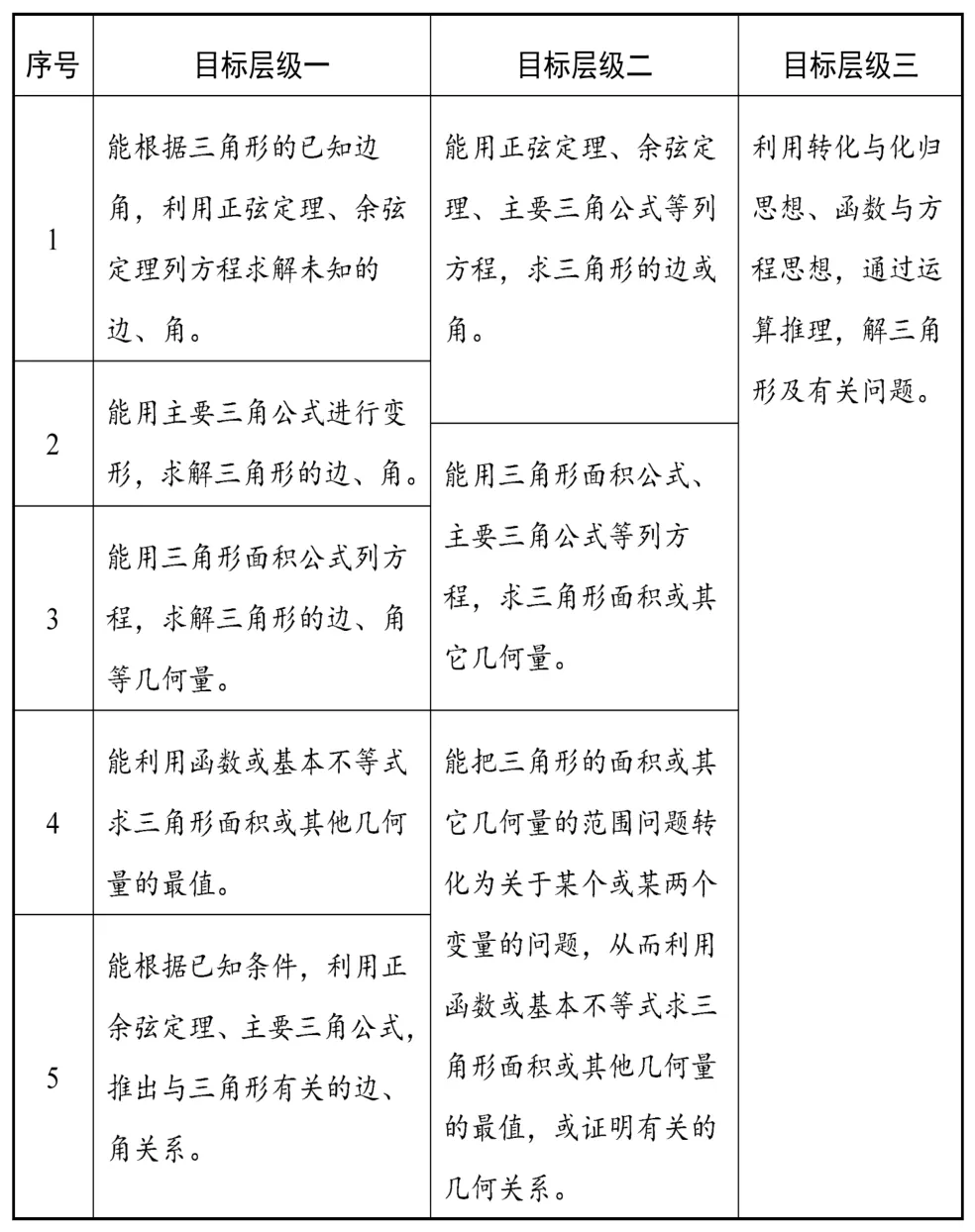
表1 三角板块具体问题、小问题与考查问题三个层级目标划分

题（Ⅰ）根据求解与三角形有关量的一般方法，应利用正弦定理将已知含有边与角的关系式“化同”为只含角的关系式，通过变形推理求B；

题（Ⅱ）根据三角形确定要素分析，在求出B的情况下，再给出b的值，并不能确定三角形，要求S的最大值，需要建立S关于某一几何量（边或角）的函数，用函数思想或基本不等式求解。

小问题：已知a，b，c分别是△ABC中角A，B，C的对边，且a2+c2-b2=ac。

（Ⅰ）求B；

（Ⅱ）若c=3a，求tan A的值。

分析：这是一个求三角形中的有关量的小问题。

根据此类问题的一般求解方法，题（Ⅰ）可直接运用余弦定理，通过变形求B；

题（Ⅱ）再加上一个关于两条边的关系式，不能确定一个三角形，要求tan A的值，可以从以下三个角度寻找解题思路：第一，从方程组的角度可以获得三条边的比例，借助余弦定理求cos A，进而得到tan A；第二，借助正弦定理，将边的关系式转化为角的关系，从而归结为只含sin A和cos A的等式，进而得到tan A；第三，先用方程的思想确定边的关系，达到化简目的，再转化为角的关系，先求sin A，进而得到tan A。以上三种思路的本质是利用正弦定理或余弦定理，通过方程的思想化归为只含“边”或“角”的关系式，这是求解“边、角”问题的基本思路。

具体问题：在△ABC中，角A，B，C所对的边分别是a，b，c。已知°，求b及A；

分析：这是一个利用正余弦定理解三角形的具体问题。

根据此类问题的一般解法，需要画出草图并根据条件判断是否能确定这个三角形，然后再正确选择公式列出方程变形推理，其中，公式的选择是关键。本题已知两边和一夹角，可根据余弦定理先求对边，再用余弦定理或正弦定理求角A。在确定的三角形中，已知两边和一对角常用正弦定理求解。因此，解题需对条件进行分析，并根据条件选择正弦或余弦定理。

二、用五环节模式设计课堂教学

高考数学复习还要回答“怎么教和怎么学”以及“教得怎样和学得怎样”的问题，这些问题最终归结为“学生在原有能力上有怎样的提升”。“能力立意，基于测评”的高考数学复习，最典型的教学特点就是“基于测评”，教学有五个环节，过程如下：（如图3）

图3 教学五环节模式

环节一：能力测评

（1）适当改编一个考查问题（体现高考能力要求），让学生阅读思考，并限时解答。

（2）出示正确答案，对学生的解答进行反馈评价。

环节二：诊断分析

根据学生群体的诊断结果，借助考查问题的三层次划分，引出考查问题所需要进一步研究的具体问题，出示课题。

环节三：典例精析

（1）选择一个能解决这个具体问题的典型例题，进行分析求解，注意问题的分析、条件的价值，如对解三角，主要考虑几何条件的理解，以及一般思维方法，注意核心知识的落实，方法的提炼，表达的规范。

典型例题教学时，应倡导“延时判断、适时概括”的教法，延时判断就是给学生充足的时间，给学生留下判断的时间，教师不急于用自己的结论代替学生的思考。适时概括强调在最佳的时间里给出方法的总结、推广和理论的提升，这对学生正确认识数学，夯实四基，发展数学核心素养，优化学习效果都有重要作用。适时概括的三个着力点分别是考查的知识、思想方法和主要能力，即通过分析条件、结论以及沟通它们的桥梁，得出考查的知识点；通过分析知识点之间的联系和转化，得出考查的思想方法和主要能力。

（2）选择该例题的一个变式训练，由学生独立解答，并进行分析讲解。

（3）对解决具体问题所需的知识和方法进行小结，关注核心思想的提炼。

环节四：课堂小结

用简短的语言对学生的学习过程进行小结，重点分析解决问题中形成的基本思维方法、蕴涵在解题过程中的思想方法。

环节五：目标检测

提供1道目标检测题，进行限时检测并反馈。

以上五个环节构成完整的一节复习课。教学从能力测评开始，借助智慧课堂收集学生的测评结果；接着，基于能力分析进行学习诊断，析出具体问题（或小问题、考查问题，下同）；再针对具体问题，选择典型例题进行精析；然后根据学习情况进行小结，完成复习教学的过程；最后，设计典型例题的变式题进行目标检测，检测学生课堂学习效果。每个环节都是为下一环节服务，最后一个环节用于检测教学目标是否完成，所以每个环节都不能缺少，也不能调整顺序。

以问题为导向，复习教学就有了能力标准，将问题分层，按能力划分层级设计教学，解决了“教什么和学什么”；五环节模式环环相扣，解决了“怎么教和怎么学”；复习教学始于“能力测评”，止于“目标检测”，两次检测的能力差异回答了“教的怎样和学的怎样”。

致谢：本文是集体智慧的结晶，特别感谢章建跃博士、白涛博士、郭慧清正高级教师及所有课题组成员。

（黄炳锋，福州第三中学高级教师，首批福建省中小学教学名师）