自动控制原理教学改革的探索与实践

史莹晶，李 瑞，赵慧洁

(电子科技大学 自动化工程学院,四川 成都 611731)

自动控制原理是电气自动化专业的主干课程之一,它面向控制对象,注重理论和实践相结合,主要研究自动控制系统中的基本理论及分析和设计方法[1-3]。该课程涉及知识面广且内容抽象、理论性强,课本中含有大量的数学公式推导及图表曲线,具有一定的学习难度和教学难度[4-5]。从这门课的教学现状来看,学生普遍感到难学和乏味[6-7]。因此寻求有效的教学方法帮助学生理解与掌握课程要求的基础概念、基本原理和常用分析与设计方法,是目前要解决的关键问题。此外,还应增强学生的工程实践意识,培养学生应用所学知识解决实际问题的能力。

大多数工科院校在开设自动控制原理课之后,会开设自动控制原理实验课,目的是借助于强大的MATLAB工具,实现对控制系统进行建模,并利用时域分析、根轨迹法、频域响应等方法对系统进行分析与设计。通过实际操作,巩固课堂知识,加深对所学内容的理解。

虽然自动控制原理实验课可以加深学生对于理论课程中所学知识的理解。然而,目前绝大多数的实验课往往首先介绍经典控制系统分析中常用的命令和SIMULINK仿真软件,在此基础上开展自动控制理论基础实验。大多实验课是以验证性实验为主,而且实验内容相对单一、陈旧,无法实现从实际系统中了解系统的结构特征、工作原理,也无法真正做到将书本上的分析方法应用到实际系统中,融汇课堂知识和实际经验,达到“学以致用”的目的。

针对当前教学中存在的问题,结合自动控制原理课程的特点,本文尝试对自动控制原理实验课进行改革。在教学中,引入工程实例,贯穿课程始终。借助于强大的MATLAB工具,将抽象的课本概念和分析方法真真切切的应用到案例中,调动学生的积极性,降低学习难度,增加学习乐趣,使教学成效得到改善,同时也增强了学生的实际动手能力和创新能力。

1 课堂教学改革和实践

目前一些自动控制原理教程已经提出了一个大例子贯穿整个教学过程[2],这种方式既有利于学生对整个课程知识框架的形成,也能随着课程的步步深入而引导学生动手实验、亲自验证,循序渐进地掌握各个知识点；还可以弥补实验课课时不足的缺陷,让学生时时刻刻都在“实际系统”中学习和思考。如在自动控制原理的实际授课过程中,可以使用磁盘驱动读取系统、锅炉液位控制系统、电阻炉温度微型计算机控制系统等作为一个大例子,贯穿整门课程的内容。

然而,上述系统仍然为抽象出来的数学模型,使学生无法真正理解所学知识点在工程中的实际应用。在本课程中,选择以四旋翼飞行器作为教学平台,将自动控制原理中的建模、分析及设计方法应用于该平台,使学生对于课程中知识点的理解更透彻,巩固了课堂知识,并达到了“学以致用”的目的。选取“四旋翼自动控制系统”作为一个大例子,一方面是由于该例子涵盖了自动控制原理中的许多关键知识点,如数学模型的建立、系统的时域响应、系统的根轨迹设计、PID控制器设计等,能够较好的、全面的串起该课程的知识点；另外,这个例子的分析也具有实用价值,尤其是进入21世纪后,四旋翼飞行器因为其体积小、造价低、使用方便等优点在军事、民用等各个领域中得到了越来越广泛的应用[8-11]；此外,作者所在团队目前正在开展四旋翼飞行器的研究,实验室拥有多架四旋翼飞行控制平台,可以使学生最终实现学以致用的目的。

1.1 案例实施方案

首先根据选课人数将学生分组。本课程有50人选课,将学生分为5组,每组10人。每组学生合作完成实验,最终提交一份实验报告。在实验过程中,鼓励学生首先独立完成实验,之后组内同学就实验结果一起分析、比较和讨论。此外,对于参与实验课的学生,每组选拔一名同学,再组成一个5人小组,进入教研室,一方面学习四旋翼飞行器的实物平台搭建,另一方面,将实验课的仿真结果应用于我们的实物平台。使学生通过实验课加深对自控原理课程及其应用前景的了解。

1.2 案例实施过程(应用举例)

本文重点介绍如何在实验课中开展对四旋翼自主飞行控制系统的建模、分析和设计等。课程中贯穿大例子,是指当课程介绍到某一知识点或方法时,可以在大例子上进行演练,形象具体的将操作步骤和结果展现出来；目的是指导学生跟随老师建立研究对象的控制模型,并在此过程中,实时的将所学到的新知识点或方法运用到模型上,进行方法演练和性能改进。

在讲授自控原理课程时,首先介绍控制系统的数学模型,即微分方程或是传递函数；在此基础上,建立时域分析方法,即通过复数域中系统输出的求取及拉式反变换求出时域响应。而根轨迹方法是一种直接由开环传递函数寻求闭环特征根移动轨迹的方法,可以通过其分析系统的三大性能。为了解决时域分析法中存在的数学模型问题、高频噪声问题等方面的不足,课程会进一步介绍频域分析法,给出重要的奈奎斯特稳定判据,分析和判断系统稳定性；对于不稳定的系统,课程中会进一步给出几种常用的校正方法,实现系统的稳定性和要求的性能指标。本课程中,将四旋翼飞控系统设计的例子贯穿于课程始末,参与到建模、分析和设计的每个环节,提升了授课效果。

下面将以实际操作的形式介绍改革后该课程的开展。这里要说明的是,在学生动手操作时,由于对模型的简化程度,参数设置的不同等因素,所得的结果是各异的。首先建立系统模型,接着对系统进行时域分析,再利用根轨迹法找到系统的稳定条件并对系统参数进行调整,然后借助波特图法和奈奎斯特法研究系统的稳定性,最后使系统稳定并达到设计要求。受篇幅所限,本文对于频域分析部分 (基于伯德图和奈奎斯特稳定性分析)以及系统校正部分不做介绍。

1)系统模型化。

大例子穿插的第一步是搭建研究对象的数学模型,主要是指根据给定的条件,搭建系统的模型。由于建立四旋翼飞行器的数学模型,需要相应的坐标系转换、动力学等知识,受篇幅所限,本文忽略了对四旋翼飞行器进行机理建模的过程,而是将四旋翼的数学模型作为已有知识。

在建立了四旋翼飞行器的数学模型后,采用通用的SIMULINK建模工具对系统进行数学符号化。这一部分主要是让学生掌握MATLAB和SIM-ULINK的使用方法。值得说明的是,熟练掌握SIMULINK建模工具是学生们未来开展系统分析与设计的基础[12]。

在本课程中,设置了高度控制和姿态控制两个主要方向,同时鼓励有余力的学生在系统模型中加入扰动等因素,实现系统的鲁棒控制。在本文中,侧重说明课程改革的具体方法,因而对“四旋翼自动控制系统”进行简化处理,只对四旋翼的高度通道进行控制,即四旋翼只做Z轴方向的运动而不考虑其他方向的运动。具体条件如下:设四旋翼的4个电机产生的合力在其纵向对称面内,额定转速下,产生的升力和四旋翼的重力相等,通过控制电机转速来控制四旋翼上升和下降。现欲使四旋翼在20 m的高度悬停,假定电机参与控制,且其初始推力线指向当地铅垂坐标系Z轴方向。建模所需参数如表1所示。

根据上述参数,在MATLAB下建立四旋翼的SIMULINK模型如图1所示。

表1 四旋翼参数表

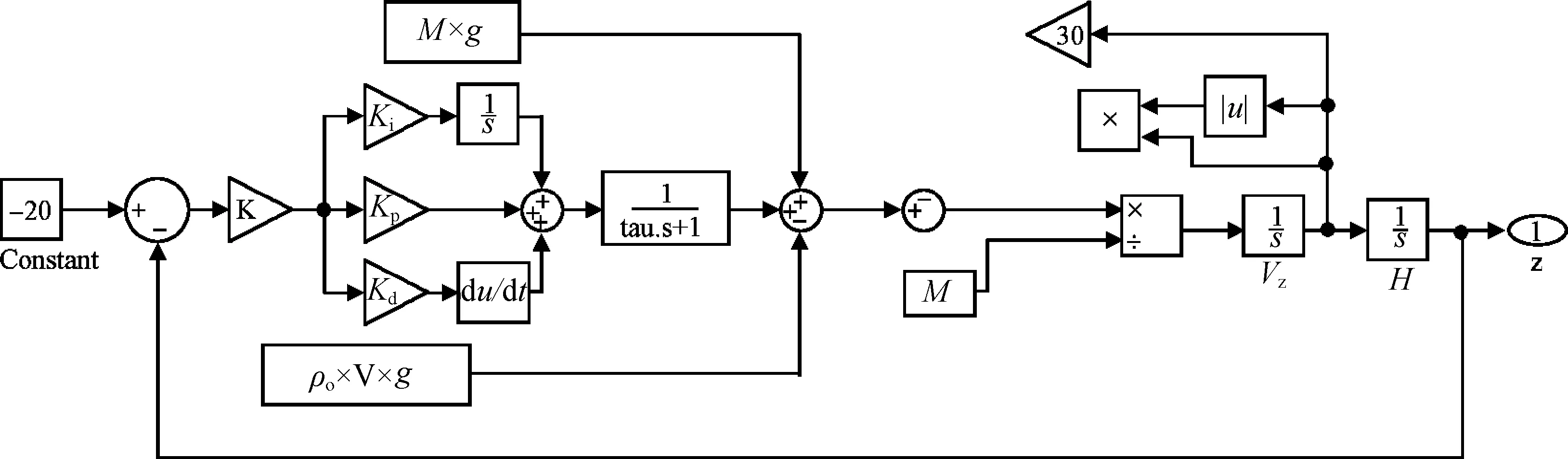
图1 四旋翼SIMULINK模型

先对模块进行初始化,代码如下:

StopTime＝100； StepSize＝0.05；

M ＝10； I＝eye(3)；

xyz＝ [0,0, -20]；

ptp＝ [0,0,0]； pqr＝ [0,0,0]；

g＝9.8； ρo＝1.18；

Kp＝1； Ki＝0； Kd＝0； K＝1；

初始化时,未对四旋翼进行控制,即模型中的PID控制律参数 K、Kp为1,而 Ki、Kd为0,此时系统的仿真结果如图2所示。

图2 无控制时飞四旋翼高度曲线

由上图可知,未加控制时,四旋翼在预设高度上下震荡,且随时间推移无法稳定。为了达到悬停的要求,需要对模型进行分析和改进。本文根据课程特点,首先对系统进行时域分析,再利用根轨迹法找到系统的稳定条件,对模型参数进行调整,使系统稳定并达到悬停的要求。

2)时域分析。

在确定系统的数学模型后,可以对控制系统的性能进行分析。本文主要利用时域分析法和根轨迹法来分析系统的性能,并根据实际系统的要求对模型进行改进。本节主要讨论时域分析法在此模型上的应用,根轨迹法将在下一小节中详细讨论。

时域分析法是在时间域中,直接对系统进行分析的方法。该方法可以提供系统时间响应的完整信息[2],且相对其他分析法来说更直观和准确,因此一直被广泛应用。下面将主要研究系统的时域响应,并根据实际系统对模型做出修改和完善。

如图1所示,本系统中,假定发动机传递函数Ga(s)近似为一阶惯性环节为了测定此系统的性能,现以单位阶跃信号驱动模型,当τ＝1时绘制系统的动态输出如图3(a)所示。

图3 传递函数修改前后系统响应曲线

由图3(a)可知,当τ＝1时,系统的单位阶跃信号的响应时间约为4 s。然而,实际系统中,要求四旋翼具有高实时性,响应时间一般在1 s内。因此需调整发动机参数,使之符合实际系统。

如图3(b)所示为调整后,τ＝0.1时的单位阶跃信号的响应曲线图,此时的响应时间约为0.5 s,符合实际系统要求。

由以上分析可知,使用时域分析法来对线性系统进行分析,可以直观、准确的体现系统的时间响应信息,也可依此来对系统进行改进。

3)根轨迹法分析及PID控制器设计。

根轨迹法是分析和设计控制系统的图解方法,应用十分方便,而且在进行具有回路的系统的分析时,应用根轨迹法比用其他方法更为灵活和方便[2]。本小节主要介绍根轨迹法在高度解算系统中的应用,再根据系统稳定条件调整PID控制器参数,使系统达到要求。

如图1所示,最终输出高度z是通过加速度两次积分得到的,即整个系统的传递函数为:

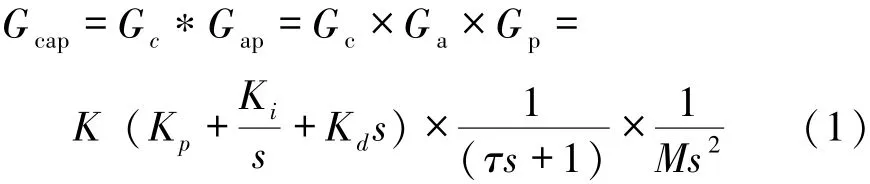
式中,Gcap为被控对象的传递函数,Gc为PID控制器表达式,Ga为电机传递函数,Gp为高度计算函数,K、Kp、Ki和Kd为PID控制器参数。

下面将利用根轨迹法调整系统参数,使系统稳定。当K、Kp为1,而Ki、Kd为0,即PID未参与控制时,此时的系统根轨迹如图4(a)所示。

由图4(a)可知,PID控制器在没有微、积分控制时,系统无法稳定。因此必须在系统中引入控制。K＝Kp＝Ki＝Kd＝1时的系统根轨迹图如图4(b)所示。

由图4(b)可知,PID控制器加入微、积分控制后,系统可以处于稳定状态。但是,不是在所有的增益下系统都是稳定的,因此要想使系统稳定,就需要选取合适的系统增益。从图中可以看出,要想使系统处于稳定状态,就需要调整系统增益在13左右,因此,取K＝15而Kp＝Ki＝Kd＝1,重新绘制系统根轨迹如图5所示。

图5 系统增益为15时的系统根轨迹

由图5可知,当K＝15时,系统处于稳定状态。因此,设定PID控制器参数为:K＝15、Kp＝Ki＝Kd＝1,进行系统仿真,结果如图6(a)所示。

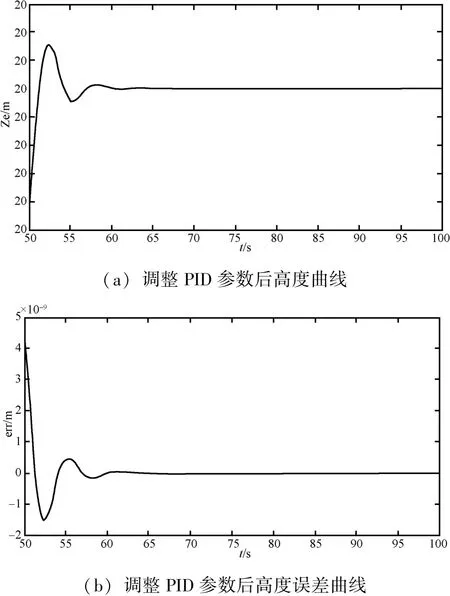
图6 调整PID参数后高度曲线及高度误差曲线

由图6(a)可看出,PID控制器参数调整后,系统可以稳定。在讲授此部分内容时,加强了对PID控制器的分析。在授课过程中,鼓励学生通过对多组实验结果进行分析,了解PID控制器中各参数对系统性能的影响及参数整定方法,为学生们后续参与实际工程项目打下基础。

高度误差曲线如图6(b)所示。从图中可以看出,误差在10-9数量级,相对于高度数据很小,可以认为符合系统要求。

根据根轨迹和系统稳定性之间的关系,可以很方便的找到系统稳定时的增益,再对PID参数进行调整,可以很快地使系统处于稳定状态。从高度仿真曲线和高度误差曲线可以看出,根据此方法设计的PID控制器可以使系统达到要求,且具有较高的精度。

对于基于奈奎斯特图和伯德图的稳定性判据等内容,受篇幅所限,这里不再介绍了。值得提及的是,本课程中开展了丰富的分析和设计内容,受篇幅所限,仅就有代表性的一些子问题给出了例证。

4)小结。

除了利用MATLAB针对四旋翼进行了建模、分析和设计,本课程中,还尝试选拔了5名同学参与实际平台的验证。在完成控制系统设计并通过仿真实验论证后,同学们在教研室学长们的帮助下将控制器加载到了实际飞行器中,进行了飞行实验验证。通过大量的实验和调试,最终实现了满意的飞行效果。

综上,这个大例子贯穿了自动控制原理的很多重要知识点,也能够很好地将课程要求掌握的各种分析、实验方法应用到实际系统中,不仅对学生掌握理论知识有很大帮助,还使学生的动手能力和分析解决问题的能力得到锻炼。

2 改革后教学成效

上述方法已经成功地运用在教学实践中,并有了一定的效果,主要体现在以下3点。

1)化抽象为具体。

引入MATLAB平台后,借助其强大的计算和绘图工具,使得公式推导、数值计算、结果展现都变得生动,将课本中抽象的概念和方法转化为具体的、可实施的、可操作的,有助于授课老师的讲解和学生的理解；另外,学生掌握了MATLAB这门数学工具,也有利于其他课程的学习和以后科研工作的开展。

2)形成系统化的思维模式。

以实际工程案例贯穿实验课程,使得学生形成系统的知识框架,从宏观出发,能够更好地把握整门课程的知识重点；且有利于练习新学到的方法和技巧,也可以巩固旧知识点。

3)提升学生科研及动手能力。

MATLAB工具结合实际工程案例,可以使学生掌握基本的数学建模、计算机辅助分析和设计方法；将仿真结果应用于实物平台,有利于提升学生的科研能力和实际操作能力,并激发学生的科研兴趣。

3 结束语

本文阐述了对于自动控制原理实验课的改革思路、实施方案及实施结果。通过在实验课中贯穿四旋翼飞行器的自主控制实例,使学生们一方面更加深入、系统的理解了自动控制原理课程的主要知识点,另一方面也使得学生了解了如何将理论知识应用于实际系统。本课程提升了学生的工程实践能力,激发了学生的科研兴趣,实施效果良好。