真在非标准算术模型中的不可定义性
2018-12-07高珂
高 珂
(北京大学 哲学系,北京 100871)
塔斯基的算术真不可定义定理(Tarski’s theorem on the undefinability of arithmetical truth)表明一阶算术真语句集在标准自然数模型上是不可定义的。通过分析证明,可以发现这一结果本质上依赖对角线引理(diagonalization lemma)的使用。根据哥德尔(Gödel)的工作,可以将元语言算术化,这样便可以定义更一般的真语句集。而利用紧致性定理(compactness theorem)很容易证明除标准自然数模型外,还存在许多非标准的一阶算术模型。本文将推广塔斯基的结果,证明通过塔斯基T-语句和语义定义构造的真语句集在可数的非标准算术模型上都是不可定义的。更进一步,这些证明将不依赖于对角线引理,这表明对于这些真语句集在模型上的不可定义性,对角线性质并不是本质的。在此基础上,最后本文还将讨论这些真语句集的相对不可定义性。
一、真语句集的定义
令一阶算术语言LA={+,·,0,1,<},PA表示皮亚诺算术(Peano arithmetic)。根据哥德尔的工作,一阶算术语言中的每个符号、公式、公式序列都有唯一的一个哥德尔编码,用符号┌┐表示,为了表述方便,一般不区分这些表达式与他们的哥德尔编码。又因为一阶算术语言下的项、句子和公式的编码构成的集合是原始递归的,所以这些集合在PA中可表示[1],分别用公式Term(x),Sent(x)和Form(x)表示。即M满足Term(n)当且仅当n是一个项的哥德尔编码。
根据塔斯基的T-语句,可以定义满足去引号性质的真语句集如下。
定义1 假设M是一个PA的模型。M的子集S是M上的T-集合,当且仅当对于所有的一阶算术公式φ(¯v),

如果模型(M,S)还满足所有LA∪{S}语言下的归纳法,那么称这样的S是一个归纳T-集合。
更一般地,通过对语言的算术化,还可以定义通过塔斯基语义定义的真语句(编码)集如下。
定义2 假设M是一个PA的模型。M的子集S是M上的一个全满足类(full satisfaction class),当且仅当对于任意满足MFrom(φ)的公式 φ以及 a∈M,(φ,a)∈S当且仅当下列某项在模型(M,S)中成立①更准确地说,这里应当是对子的编码属于S,为了表述方便一般不区分对子与它的编码,希望不会引发歧义。。
T1(φ,a):∃t∃s(Term(t) Term(s) φ=(t=s) val(s)=val(t));
T2(φ,a):∃t∃s(Term(t) Term(s) φ=(t<s) val(s)<val(t));
T3(φ,a):∃ψ(Form(ψ) φ= ψ (ψ,a)∉S);
T4(φ,a):∃ψ1,ψ2(Form(ψ1) Form(ψ2) φ=(ψ1ψ2)((ψ1,a)∈S (ψ2,a)∈S));
T5(φ,a):∃ψ1,ψ2(Form(ψ1) Form(ψ2) φ=(ψ1ψ2)((ψ1,a)∈S (ψ2,a)∈S));
T6(φ,a):∃i,ψ(From(ψ) φ=∃viψ ∃b((ψ,a[b/i])∈S));
T7(φ,a):∃i,ψ(From(ψ) φ=∀viψ ∀b((ψ,a[b/i])∈S)),
其中,val是PA下可定义的赋值函数,a是φ中参数的编码,a[b/i]表示用b替换a解码得到的参数序列中的第i个元素后得到序列的编码。
定义3 M的子集S是M上的一个部分满足类(partial satisfaction class),当且仅当对于任意满足MFrom(φ)的公式 φ以及 a∈M,(φ,a)∈S当且仅当存在 M中的非标准元 c,使得任意 φ<c,(M,S)
类似地,如果一个M上的部分(全)满足类S使得模型(M,S)还满足所有LA∪{S}语言下的归纳法,那么我们称这样的S是一个归纳部分(全)满足类(inductive partial(full)satisfaction class)。
定义4 一个M的子集X在模型M上是可定义的,当且仅当存在一个公式φ(x,¯a)和一组给定的有穷参数¯a∈M使得

二、算术模型的递归饱和性
拉克兰(Lachlan)、科特拉尔斯基(Kotlarski)和克拉热夫斯基(Krajewski)在20世纪80年代的工作表明,当M是一个可数的非标准一阶算术模型时,模型上的全满足类与模型的递归饱和性之间存在着密切联系。
定理1 (拉克兰,1981)假设M是一个可数的非标准一阶算术模型。如果M上存在一个全满足类,那么M是递归饱和的[2]。
定理2 (拉克兰、科特拉尔斯基和克拉热夫斯基,1981)如果M是一个可数的一阶算术模型并且M是递归饱和的,那么M上一定存在一个全满足类[3]。
推广拉克兰等人的结果到归纳部分满足类与归纳T-集合上,可以证明定理1和定理2结论依然成立。在证明上述命题之前,本小节将先给出一些模型递归饱和性相关的概念和性质。
定义5 假设L是可数的一阶语言,M是任意L-模型,b¯∈M是一组给定的有穷参数。
1.L-公式集p(v,¯b)={φi(v,b¯)∶i∈N}是M上的型,当且仅当p(v,b¯)在M中有穷满足,即对于任意自然数构成的有穷集I,都存在M中的元素a使得对于任意I中的元素i都有Mφi(a,b¯)。
2.一个型p(v,b¯)是递归的,当且仅当集合
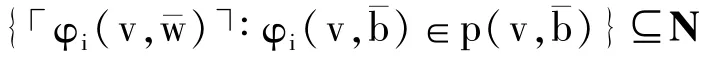
是递归的,这里¯w是一串有穷长的变元。
3.M是递归饱和的,当且仅当所有M上的递归型都在M中被实现。
通过下列性质,很容易得知,并非所有的可数算术模型都是递归饱和的。
性质1 有穷生成的模型不是递归饱和的。
证明:假设K是有穷集合{a0,…,an}的斯克伦闭包,那么K中的元素都应该形如t(a0,…,an),其中t是斯克伦项,考虑如下递归集
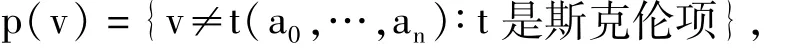
显然,p(v)的有穷子集都在K中被实现,所以p(v)在K中有穷满足,依定义p(v)是M上的递归型,但同时p(v)在K中无法实现,所以K不是递归饱和的。
定义6 假设L是一个一阶语言。
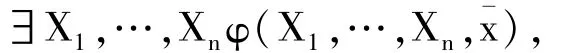
其中,X1,…,Xn是新的关系或运算符号,φ(X1,…,Xn,¯x)是扩充后的语言L∪{X1,…,Xn}下的公式。如果φ(X1,…,Xn,¯x)中没有自由的一阶变元,那么∃X1,…,Xnφ(X1,…,Xn)是一个∑11句子。一个L-模型满足句子 Φ=∃X1,…,Xnφ(X1,…,Xn)当且仅当存在一个 M的膨胀(M,X1,…,Xn)使得
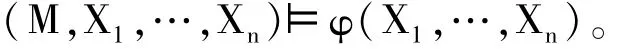
2.如果T是一个一阶理论,那么T+Φ是一致的当且仅当存在一个满足T的一阶模型的膨胀满足T+φ(X1,…,Xn)。
3.一个L-模型M是华丽的当且仅当对于所有有穷长的参数¯a∈M以及LU{¯a}语言下的句子Φ(¯a),都有:

根据克林尼(Kleene)、巴维斯(Barwise)和施利普夫(Schlipf)给出的结果,对于可数的算术模型而言,模型的华丽性与递归饱和性是等价的,这一性质在以后的工作中将起到重要作用。
命题1 (巴维斯和施利普夫,1975)假设L是一个递归语言,M是L语言下的可数递归饱和模型,¯a∈M是一组有穷的参数,语言L′是语言L∪{¯a}的一个递归扩张,T是一个L′语言下递归可公理化的理论。如果Th(M+¯a)+T是一致的,那么存在一个(M,¯a)在L′语言下的膨胀满足T[4]。
命题2 (克林尼,1952)假设L是一个只包含有穷多的关系、函数和常元符号的一阶语言。令{θi(¯x)∶i∈N}是一个由L-公式构成的递归集,其中对任意标准自然数i,θi(¯x)上都只有有穷的自由变元。存在一个L语言下的公式Φ(¯x)使得,对任意无穷L-模型M,有

定理3 任给可数的一阶算术模型M。M是递归饱和的当且仅当M是华丽的。
证明:因为一阶算术语言包含的关系、函数和常元符号都是有穷的,由命题2可得,如果一个可数的一阶算术模型是华丽的,那么它一定是递归饱和的。上述结果结合命题1即所求。
三、真语句集与模型的递归饱和性
本小节将主要证明对定理1和定理2的推广。
定理4
a.假设M是一个可数的非标准一阶算术模型,M上存在一个归纳部分满足类当且仅当M是递归饱和的。
b.假设M是一个可数的非标准一阶算术模型,M上存在一个归纳T-集合当且仅当M是递归饱和的。
先给出一些必要的技术性结果。
性质2 (溢出原则)假设M是一个非标准的一阶算术模型,a¯∈M是一组给定的有穷参数,φ(v,a¯)是一个标准一阶算术公式。如果对于任意自然数n,都有Mφ(n,a¯),那么一定存在一个M中的非标准元 b,使得

证明:假设不存在这样的非标准元,即对于所有M中的非标准元b,都没有M∀i≤bφ(i,a¯)。
验证,对于任意M中的元素c,有∀y≤cφ(y,a¯)→∀y≤c+1φ(y,a¯)。当c是标准自然数时,上述命题显然成立。又根据假设,如果有∀y≤cφ(y,a¯),那么c一定是标准的,那么由标准自然数的性质可知c+1也一定是标准的。
根据上述论述,就会有
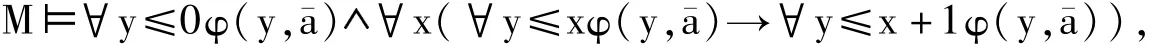
性质3 假设M是一个非标准一阶算术模型,S是一个M上的部分(全)满足类,φ(v0,…,vn)是只带有自由变元v0,…,vn的标准一阶算术公式,那么对所有的M中的元素a,

证明:对标准一阶算术公式φ的复杂度施归纳,由满足类的定义与赋值函数的性质易得。
首先证明定理4a。
命题3 假设模型M是一个可数的非标准一阶算术模型。如果M上存在一个归纳部分满足类,那么M是递归饱和的。
证明:假设S是M上的一个归纳部分满足类,p(v)是M上的递归型,不失一般性地,可以假设p(v)中只带有一个自由变元且p(v)中不带参数。因为p(v)是递归的,所以存在M中的元素b,使得p(v)被b编码。那么对于任意标准自然数n,我们都有

因为S是可归纳的,根据溢出原则,M中一定存在非标准元c,使得

根据性质3,任意M中的元素d,只要d满足上述公式,那么d就实现p(v)。
接下来证明定理4a的另一个方向。
引理1 如果模型M是一个可数的非标准算术模型,那么存在可数模型N使得N是M的初等扩张并且N上有一个归纳部分满足类。
证明:令¯M=M∪{ca∶a∈M},其中ca是新的常元符号。再令T是如下理论:

其中,φ是标准的一阶算术公式。
首先验证T是一致的。
取T的有穷子理论T′,使得T′中包含的任意公式θ的哥德尔编码都小于某个自然数n,定义M的子集 S′如下

其中,令iθ表示出现在θ中的自由变元的最大指标。显然,S′在M中可以被一个标准一阶算术公式定义,所以(M,S′)满足扩张后语言下公式的归纳法,又因为所有哥德尔编码小于给定n的公式构成的集合对子公式封闭,所以(M,S′)满足T′,再根据紧致性定理,就得到了T是一致的。
令(N,S″)是T的模型,N是可数的。根据T的定义,N是M的初等扩张。接下来只需证明存在N中非标准元b,使得S″限制在<b上是一个归纳部分满足类。
根据定义,对于任意标准自然数n,都有

又因为这是一个扩张后语言下的公式,而(N,S″)满足所有扩张后语言下公式的归纳法,所以溢出原则对这个公式有效。所以,存在N中的非标准元b使得

令 S={(φ,a)∶φ<a (φ,a)∈S″}。显然,S在(N,S″)中是可定义的,所以(N,S)满足归纳公理。这样,S就是N上的一个归纳部分满足类。
命题4 如果M是一个可数的一阶算术模型并且M是递归饱和的,那么M上一定存在一个归纳部分满足类。
证明:根据定理3,模型M是华丽的。而“存在一个归纳部分满足类”可以表示为
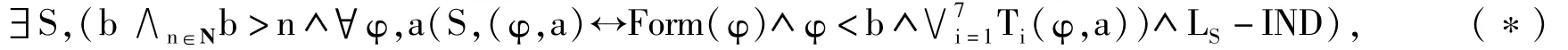
其中,LS-IND表示扩张后语言LA∪{S}下的归纳公理。(*)中的无穷合取都是递归的,所以这些无穷合取等价于一个公式,所以(*)等价于一个公式,根据引理1可得Th(M)+(*)是一致的,又根据华丽性的定义,M满足(*),也就是M上存在一个归纳部分满足类。
类似地,可以证明定理4b如下。
命题5 假设M是一个可数的非标准一阶算术模型。如果M上存在一个归纳T-集合,那么M是递归饱和的。
证明:假设S是M上的一个归纳T-集合,p(v)是M上的递归型。类似命题3可以得到存在M中的非标准元c,使得

又根据定义,T-集合中的都是标准的一阶算术语句,所以对于任意的自然数n都有Mφn(c,a¯)。这样我们就找到了一个c使得递归型p(v)在M中被实现。
引理2 如果M是一个可数的非标准一阶算术模型,那么存在可数模型N使得N是M的初等扩张并且N上有一个归纳T-集合。
证明:令T=Th(¯M)+LS语言下公式的归纳法+∀y(S(φ,y)↔φ(y)),其中φ是标准的一阶算术公式。类似引理1可得。
命题6 如果M是一个可数的算术模型并且M是递归饱和的,那么M上一定存在一个归纳T-集合。
证明:“存在一个归纳T-集合”可以表示为
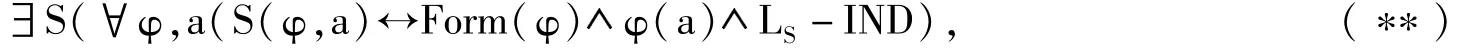
其中,LS-IND表示扩张后语言LA∪{S}下的归纳公理。与命题4类似,(**)是一个公式。再根据引理2,可知(**)与Th(M)是一致的。最后,由华丽性的定义可得,M上存在一个归纳T-集合。
四、真语句集的不可定义性和相对可定义性
利用上一小节的结果,本节将证明全满足类、部分满足类与归纳-集合在非标准算术模型上的不可定义性,特别地,这些证明将不依赖于对角线引理。此外,本小节还将讨论上述集合的相对可定义性。
如果有对角线引理,根据塔斯基真不可定义定理和性质3,很容易得到部分满足类在算术模型上的不可定义性结果。
定理5 假设M是一个可数的非标准一阶算术模型,S是一个M上的部分满足类,那么S在M中不能被标准算术公式定义。
证明:假设S可以被标准一阶算术公式φ(x,y,¯a)定义,¯a∈M是一组给定的有穷参数。根据性质3,对于所有的标准算术公式ψ,都会有

其中,[¯a]是¯a的编码。这与塔斯基算术真不可定义定理矛盾。
因为塔斯基的算术真不可定义定理本质上依赖于对角线引理,所以在定理5的证明中,对角线引理是本质的,如此,定理5可以被视作对角线引理的一个直接推论。
下面以归纳-集合为例,给出一个不依赖于对角线引理的不可定义性的证明。
定理6 假设M是一个可数的非标准一阶算术模型,S是一个M上的归纳T-集合,那么S在M中不能被标准算术公式定义。
证明:假设S可以被一个带有有穷参数a0,…,an的标准一阶算术公式定义。令K是上述有穷参数的斯克伦闭包,那么K是M的初等子模型,所以S限制在K上是一个K上的归纳T-集合,根据定理4b,K是递归饱和的,但是由性质1,K不可能是递归饱和模型,这就导致了矛盾。
归纳部分满足类和全满足类在算术模型上的不可定义性可以用同样的证明思路获得。
定理7 假设M是一个可数的非标准一阶算术模型,S是一个M上的归纳部分满足类或全满足,那么S在M中不能被标准算术公式定义。
接下来的定理表明,尽管全满足类、部分满足类和T-集合都是在可数的非标准一阶算术模型上不可定义的,但他们之间存在着某种相对可定义性。先给出一些必要的预备知识。
定义7 假设M和N是两个一阶算术模型,称M是N的尾节扩张当且仅当N是M的子模型并且N对于M的序关系向下封闭。如果N是M的真子集,则称N是M的真尾节扩张。
定理8 (麦克道威尔-施佩克尔定理(MacDowell-Specker Theorem))任意一阶算术模型都有一个真的初等尾节扩张。
更多算术模型尾节的细节,可以参看凯伊(Kaye)的专著[6]。
定理9 假设M是一个可数的非标准一阶算术模型。如果M上存在一个归纳部分满足类S,那么M上一定存在另一个归纳部分满足类S′使得S′在模型(M,S)中可定义。
证明:根据扩张后语言下的麦克道威尔-施佩克尔定理,存在(N,S″)使得(N,S″)是模型(M,S)的初等尾节扩张。根据定义很容易验证,S″是 N上的归纳部分满足类。令S′等于S″限制在M上。因为(N,S″)是(M,S)的初等尾节扩张,所以 S′在(M,S)中可定义并且是归纳的。
接下来只需证明S′是一个部分满足类。依定义验证,其他的条件都是平凡(trivial)成立的,唯一的困难在于带有量词的情况。这里,只处理存在量词,全称量词可以类似得到。考虑公式Φ(n,X)定义如下

显然,标准的一阶算术语句φ使得Φ(φ,S′)成立,而φ被标准自然数编码。这样我们就有

分析上述定理的证明,很容易发现将定理的条件改成“M上存在一个全满足类”或者“M上存在一个T-集合”,结果依然成立。这样,可以将定理8推广到更一般的结果上。
定理10 假设M是一个可数的非标准一阶算术模型。如果X是M上的一个不可定义集并且M上存在X可以推导出M是递归饱和的,那么M上一定存在一个归纳部分满足类S使得S在模型(M,X)中是可定义的。
证明:由定理4a和定理9可以直接得到。
一个自然的问题是,除了可以推导出模型递归饱和性的不可定义集,是否存在别的不可定义集,使得存在一个在扩充模型上可定义的归纳部分满足类。
接下来我们给出一个否定的结果,证明在用科恩力迫(Cohen forcing)构造的不可定义集扩充得到的模型上不存在可定义的归纳部分满足类。通过这个结果,我们似乎有理由相信能够推出模型的递归饱和性是使得某个归纳可满足类在扩充后模型上可满足的必要条件。
定义8 给定一个模型M,令2<M是由可定义函数p∶{0,…,a}→{o,1}构成的集合,其中a是M的元素。
(1)一个集合D⊆2M是稠密的当且仅当对于任意p∈2<M存在一个q∈D使得p⊆q。
(2)一个集合G⊆<M是脱殊的(generic)当且仅当
a.对于所有的G的元素p,q,p和q都可比;
b.对于所有的G的元素p和所有的M的元素a,p限制在a上属于G;
c.对于所有的可定义稠密集D,G和D的交非空。
(3)给定一个G是脱殊的,令XG={x∈M∶∃p∈G(p(x)=1)}。称XG是M的一个脱殊子集。
下列性质可以在奥德弗雷德(Odifreddi)的专著[7]中找到,这里省略具体证明。
性质4 假设M是一个一阶算术模型,则有:
(1)如果M是可数的,那么M上有一个脱殊集。
(2)脱殊集在模型M中是不可定义的。
(3)脱殊集在模型M中是归纳的。
(4)如果X是M的一个脱殊子集,那么存在一个M的不可定义子集Y,使得Y在模型(M,X)中可定义,但同时X在模型(M,Y)中不可定义。
从性质1和定理4a我们可以得到并非所有的可数非标准算术模型上存在一个归纳部分满足类,又由性质4中的(1)得所有可数的算术模型上都存在一个脱殊集。这样我们就可以得到以下的结果。
性质5 如果M是一个可数的非标准一阶算术模型,那么M上的所有归纳部分满足类都不是脱殊的。
证明:假设S是M上的一个归纳部分满足类,并且S是脱殊的。根据扩张语言下的麦克道威尔-施佩克尔定理,存在(N,S′)使得(N,S′)是(M,S)的一个初等尾节扩张。给定一个 N中的非标准元 a,令 S″等于S′限制在<a上,根据尾节扩张的性质,S″在 N中是可以被编码的,令 b是 S″的编码。令 K是M∪{b}的斯克伦闭包。很容易验证S″可以被拓展成一个集合G,使得G在K中是脱殊的。又根据力迫的一般性质,我们可以得到模型(K,G)是模型(M,S)的一个初等扩张,所以G是K上的一个归纳部分满足类。另一方面,根据构造可知,K是一个有穷生成模型的共尾扩张,类似性质1可以证明这样的模型不是递归饱和的,又由定理4a可知,K上不存在归纳的部分满足类,这就导出了矛盾。
下列的结果表明,在可数的算术模型看来,归纳部分满足类的不可定义性要“强于”脱殊集的不可定义性,这也在某种程度上说明了“真”的定义需要极高的要求。
定理11 假设M是一个可数的非标准一阶算术模型。如果G是M上的一个脱殊子集,那么不存在M上的归纳部分满足类S使得S在模型(M,G)中可定义。
证明:假设存在这样的归纳部分满足类,可以利用性质5一样的思路来构造矛盾。
定理12 假设M是一个可数的非标准一阶算术模型。如果M上存在一个归纳部分满足类S,那么M上一定存在一个脱殊子集G使得G在模型(M,S)中可定义。
证明:只需要验证“存在脱殊集”可以被形式化到模型(M,S)中。
结合性质4中的(4)和定理12,我们还能进一步得到某种归纳部分满足类上的切分性质。
推论1 假设模型M是一个可数的非标准一阶算术模型。如果M上存在一个归纳部分满足类,那么一定存在一个M上的不可定义子集X使得在模型(M,S)中可定义,但是S在(M,X)中不可定义。
而根据定理11,我们还可以得到推论1的加强版。
推论2 假设M是一个可数的非标准一阶算术模型。如果M上存在一个归纳部分满足类S,那么一定存在一个M上的不可定义子集X使得X在模型(M,S)中可定义,但是不存在M上在模型(M,X)中可定义的归纳部分满足类。
五、总结
通过继续克兰、科特拉尔斯基和克拉热夫斯基的工作,得到了如下结果。
定理13 如果M是一个可数的非标准一阶算术模型,那么下列命题两两等价:
(1)M是一个递归饱和模型;
(2)M上存在一个全满足类;
(3)M上存在一个归纳部分满足类;
(4)M上存在一个归纳T-集合。
在此基础上,本文推广塔斯基的结果,证明了全满足类、部分满足类、部分归纳满足类以及归纳-集合在可数的非标准算术模型上都是不可定义的。需要注意的是,本文只证明这些集合在可数算术模型上的不可定义性,这并不能直接推导出塔斯基算术真不可定义定理。而通过对上述集合的相对不可定义性的分析,发现对于可数非标准算术模型而言,集合在模型上的存在性可以推出模型的递归饱和性这一性质,是使得某个归纳部分满足类在以这个集合做扩张的模型上可定义的充分条件。进一步地,证明了归纳部分满足类在用科恩脱殊集做扩张得到的模型上是不可定义的,所以我们有理由猜测集合的存在性可以推导模型的递归饱和性也是保证归纳部分满足类可定义的必要条件。
最后,本文将以一些开问题作为结束。
问题1 给定一个可数的非标准一阶算术模型,在上面是否存在别的归纳不可定义集使得某个归纳部分满足类在用上述不可定义集扩张得到的模型上是可定义的?
斯莫林斯基(Smorynski)证明了存在满足上述要求的不可定义集[8],但斯莫林斯基的结果不是归纳的,是否存在这样的归纳不可定义集仍是个开问题。
问题2 将定理9结论中的归纳部分满足类换成全满足类或者-集合,定理9是否依然成立?
