微元观点在电磁感应中的应用

广东 周 璐 李 周

高中物理阶段，尽管微积分的应用并不广泛，但“微元”“累加”“无限细分”等思想却有着相当程度的应用。在电磁感应的应用中，一些模型下的求解诸如：运动的速度、回路电荷量、回路的焦耳热等问题必须考虑使用“微元观点”。本文介绍微元观点在电磁感应中的典型应用，并总结各种方法的适用范围。

2018年高考数学《考试大纲》中明确指出：导数及其应用(微积分的应用)作为高考必考的二十一个章节之一，考纲中将其列为第十七章，系人教版教材选修2-2的第一章。2018年的《考试说明》强调考查导数的概念、几何意义、运算及应用，重点考查利用，导数的方法研究函数的单调性、极值，研究方程和不等式，不要求学生具备灵活运用的能力。因此，在高中物理的命题过程中，是不会涉及必须用微积分来解决的问题。然而，在高中物理课程中，有相当一部分的物理概念的定义和公式的完整推导，比如加速度、瞬时速度、匀变速直线运动的位移、电磁感应中感应电动势等，其实是依赖于微积分的。

而在实际的问题讲授或解释中，比如变力做功，人船模型中的位移问题，动量定理求解流体问题，电磁感应中求解电荷量问题等，教师们会尽量利用“微元”“累加”等思想去呈现问题的逻辑。在近几年的高考试题中，对此类思想的考查也有加强的趋势。本文试图从电磁感应中几道典型例题出发，展示微元的观点在电磁感应中几种比较具有代表性的应用，简略总结相关方法的优点及局限性。

一、微元观点求解回路电荷量

【例1】如图1所示，水平放置的间距为L的光滑金属轨道间存在竖直向下的匀强磁场B，其左侧连接一阻值为R的电阻，一质量为m，电阻为r的导体棒垂直平放于轨道上，某时刻获得一向右的初速度v0,轨道电阻忽略。求初始时刻到最终停下，经过导体棒的电荷量q。

图1

【分析】在电磁感应中，求某过程经过回路中电荷量q是一类常见的问题，一般求变化电流背景下电荷量q的主要方法是

此方法的关键是求解过程中回路磁通量的变化ΔΦ，显然此题的运动既非匀速运动，也非匀变速运动，因此无法从运动学求解其位移，故此方法无法求解上述问题。

【解析】取向右运动为正方向，应用“微元”理论，对运动过程无限细分，取其中一段时间为Δt运动微元，对导体棒用动量定理可得：

-BILΔt=mΔv，其中Δq=IΔt①

对所有运动微元作同样计算，然后累加

-BL∑Δq=m∑Δv②

可得-BLq=m(0-v0) ③

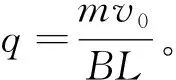
【总结】在电磁感应所涉及的运动过程中，安培力的冲量可以和经过回路的电荷量联系起来-BILΔt=-BLΔq,若已知物体运动始末的动量变化，即可以利用动量定理求解电荷量q。

【变型】如图2所示，水平放置的间距为L的光滑金属轨道间存在竖直向下的匀强磁场B，其左侧连接一电容为C的电容器，一质量为m，电阻为r的导体棒垂直平放于轨道上，某时刻获得一向右的初速度v0,轨道电阻忽略。求初始时刻到运动稳定的过程中，经过导体棒的电荷量q。

图2

【分析】从导体棒向右运动过程中，左侧电容器电量增加，极板间电压不断升高，右侧导体棒会受到向左的安培力而减速，所产生的感应电动势不断减小，当左右两侧“电动势”相等时，充电停止，安培力消失，导体棒以此时匀速向右运动下去。

【解析】设运动稳定时导体棒的速度为v，电容器上的带电荷量为q,则

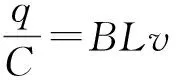
取向右为正方向，对运动过程无限细分，选其中一个运动微元，由动量定理可得

-BILΔt=mΔv，其中Δq=IΔt②

对所有运动微元作同样计算，然后累加

-BL∑Δq=m∑Δv③

可得-BLq=m(v-v0) ④

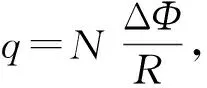
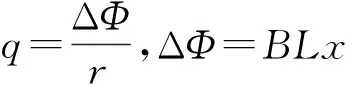
二、微元观点求解变加速运动的速度

【例2】如图3所示，光滑绝缘桌面上，一边长为L，总电阻为R，质量为m的单匝正方形线框以初速度v0向右运动，虚线右侧有竖直向下的匀强磁场B，若线框能完全进入磁场，则线框完全进入磁场的速度v为多少？

图3

【解析】取向右运动为正方向，对运动过程无限细分，取其中一运动微元，由动量定理可得

-BILΔt=mΔv①

对所有运动微元作同样计算，然后累加

【总结】在电磁感应所涉及的运动中，关于安培力的冲量微元的变型，不仅有例1中提到的，可以关联到回路中电荷量q，而且可以和运动的位移x有关联。

三、微元观点求解回路焦耳热

(1)整个运动过程中，经过回路的电荷量q。

(2)整个运动过程中，回路的焦耳热Q。

图4

【解析】(1)运动过程中，初始时刻E>BLv0，则导体棒应向右加速运动，直到

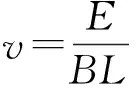
此时回路中的电流消失，导体棒速度达到最大。

对运动过程无限细分，取其中一运动微元，由动量定理可得

BILΔt=mΔv，其中Δq=IΔt②

对所有运动微元作同样计算，然后累加

BL∑Δq=m∑Δv③

可得BLq=m(v-v0) ④

(2)回路的能量来源于电源，在时间微元Δt内，电源消耗的总能量为

ΔE电=EIΔt=EΔq⑥

联合④式，累加上式可得

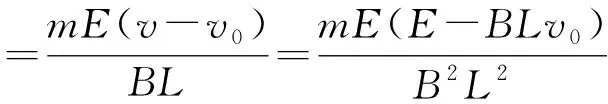
电源消耗的能量，一部分转化为回路的焦耳热Q，另一部分转化为导体棒的动能，即

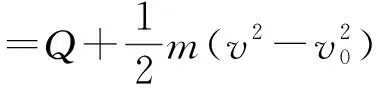
联合①⑥⑦可解得

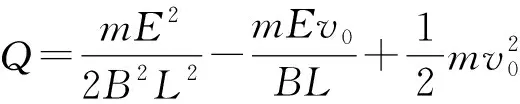
【问题延伸】在高中电磁感应的学习中，许多资料书中或者教师在教学过程中都会提到一个结论：|WF安|=Q,即电磁感应中，安培力做功的大小等于回路中的焦耳热。于是在上述问题的课堂讲解后，就有相当多的同学提出，能否利用上述结论来解决上题中的第二问

【问题解释】对于这个问题，需加以强调，因为在电磁感应章节的实际教学中，尽管教科书中没有给出此结论，但在实际的解题过程中却有大量用到，实际上此结论也有一定的实用范围。我们先来看一下上述结论的证明过程

安培力做功微元ΔWF安=BILΔx，而Δx=vΔt

则ΔWF安=BLvΔq

总电阻为R的回路中，焦耳热微元ΔQ=I2RΔt，而 Δq=IΔt

则ΔQ=IRΔq

四、方法的总结及局限性说明

在高中物理的课程设置中，尽管对于微积分的全面应用能力不作要求，然而关于“微元”“无限细分”“累加”等思想仍有一定要求，特别是在高三总复习阶段，有些电磁感应中的题目，“微元”观点的应用几乎是解决问题的唯一途径。本文中，首先列举电磁感应中安培力冲量微元的两种变式，以展示冲量微元与回路电荷量q和运动速度之间的关联

-BILΔt=-BLΔq

1.本文对求解回路中电荷量q存在两种常见方法做了简单总结：

(1)利用上述变型再结合动量定理

此种方法要求，知晓运动过程中物体的动量的变化，而且，若物体除安培力外，还受到其他力作用，则此种方法可能会因缺少条件而难以达到目的。

(2)利用结论

此种方法要求回路中电动势必须为感应电动势，若含有电容器或直流电源，此结论并不适用。

2.在电磁感应用运动中，很多运动都是变加速度运动，因此位移、时间、速度等运动学信息难以求解，上述的变型为我们提供了一种简单电磁感应运动中位移与速度之间的关联，但值得注意的是此种变型要求回路电动势E=BLv。

BILΔx=I2RΔt

3.在电磁感应过程中，关于安培力做功大小和回路所产生热量的关系，有资料书中给出了WF安=Q的结论，但从上述推导过程中可以见到，此结论成立的前提仍是回路电动势E=BLv。特别注意若回路中含有电容器，直流电源等，结论不可直接使用。