杆—容模型构建与分析策略
2018-12-07福建郑行军
福建 郑行军
在含有电容器的电磁感应电路中,由于导体杆做变速运动产生变化的电流,使得电容器会发生充电或放电现象,呈现与纯电阻电路不同的题类特征,分析过程较为复杂,其中对于电容器充放电过程的电流计算,学生更是无从下手。因此探究杆—容模型的习题编制,寻找其中的规律,对了解动生类问题在不同电路环境下的动力学、功能关系特点有一定的帮助。
题型一、充电式电容器+无外力推动式切割问题
【例1】如图1甲所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为l,电阻均可忽略不计。在M和P之间接有阻值为R的定值电阻,导体杆ab质量为m、有效电阻为r,并与导轨接触良好。整个装置处于方向竖直向上磁感应强度为B的匀强磁场中,现给ab杆一个初速度v0,使杆向右运动。则
( )

B.通过电阻R的电流I随时间t的变化率的绝对值逐渐增大
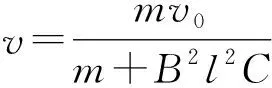
D.在C选项中,杆稳定后a端电势低于b端电势

图1

【答案】AC
【点评】将导轨之间的电阻改为电容器时,ab杆稳定产生的电动势等于电容器两端的电压,结合电容器的定义式,运用牛顿运动定律或动量定理,采用微元的思想即可求出ab杆稳定后的速度。对于一般的电磁感应问题研究思路有两条:一是从力的角度,重点是分析安培力作用下物体的平衡问题;二是能量角度,重点是分析现象中的能量转化,这是解题的关键。
题型二、充电式电容器+外力推动式切割问题
【例2】如图2所示,处于匀强磁场中的两根足够长且电阻不计的平行金属导轨相距L,导轨平面与水平面重合,左端用导线连接电容为C的电容器(能承受的电压足够大)。已知匀强磁场的磁感应强度大小为B、方向竖直向上。一质量为m、电阻不计的直金属棒垂直放在两导轨上,一根绝缘的、足够长的轻绳一端与棒的中点连接,另一端跨过定滑轮挂一质量为m的重物。现从静止释放重物并通过轻绳水平拖动金属棒运动(金属棒始终与导轨垂直并保持良好接触,不计滑轮质量和所有摩擦)。求:
(1)若某时刻金属棒速度为v,则电容器两端的电压多大;
(2)求证:金属棒的运动是匀加速直线运动;
(3)当重物从静止开始下落一定高度时,电容器带电荷量为Q,则这个高度h多大?

图2
【解析】(1)电容器两端的电压等于导体棒切割产生的感应电动势,得U=E=BLv。
(2)设经过很短的时间Δt时,金属棒速度变化设为Δv,金属棒切割磁感线产生电动势变化ΔE=BLΔv
电容器两端电压的变化ΔU=ΔE=BLΔv
电容器所带电荷量变化为Δq=C·ΔU=CBLΔv

对物体m:mg-F拉=ma
对棒:F拉-BIL=ma

式中各量都是恒量,加速度保持不变,故金属棒的运动是匀加速直线运动。

【点评】本题为杆—容充电式问题,综合电磁感应与力学的相关知识,解题关键在于运用电流的定义式确定电容器充电电流,根据法拉第电磁感应定律求感应电动势;根据牛顿第二定律或动量定理推导证明;结合电荷量的公式进行求解。
题型三、放电式电容器+动杆切割问题
【例3】某同学设计的“电磁弹射”装置如图3所示,足够长的光滑金属导轨(电阻不计)水平固定放置,间距为l,磁感应强度大小为B的磁场垂直于轨道平面向下。在导轨左端跨接电容为C的电容器,另一质量为m、电阻为R的导体棒垂直于导轨摆放。先断开开关S,对电容器充电,使其带电荷量为Q,再闭合开关S,关于该装置及导体棒的运动情况下列说法正确的是
( )

图3
A.要使导体棒向右运动,电容器的b极板应带正电
C.导体棒运动过程中,流过导体棒横截面的电荷量为Q
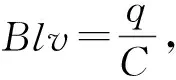
【答案】B
【点评】开关闭合后在安培力作用下运动,由导体棒的运动方向可判定电流方向,进而可知电容器两极板电性;导体棒运动时将形成与原电流相反的感应电动势,同时电容器两端电压降低,导体棒两端电压升高,当二者相等时,导体棒匀速运动运动速度最大。该题的关键是判定最大速度,要明确其条件是感应电动势等于电容器两端的电压,结合牛顿运动定律或动量定理求解。
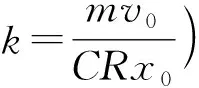
(1)从杆开始运动至到达P点F所做的功和电阻R上放出的热量;
(2)磁感应强度B的大小;
(3)越过P点后杆粘上物体(物体离开水平面)成为一体,并让ab杆维持速度v0匀速运动一段足够长的时间后撤去外力,那么撤去外力后杆运动多长时间才能停止运动?撤去外力后杆运动了多长的距离?
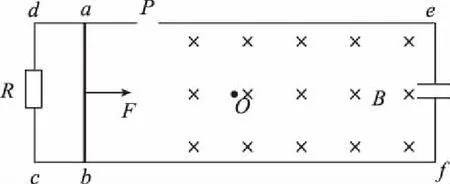
图4
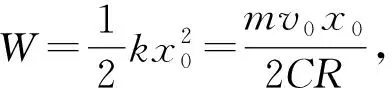
(2)因为杆无质量,故拉力必然时刻等于安培力,有
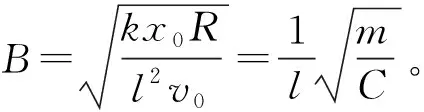

μmgΔt-BlΔq=m|Δv|
Δq=CΔU=CBl|Δv|
其中|Δv|=v0-v
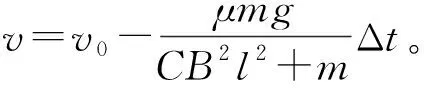
得CB2l2=m