从一道题来看运动过程模型在处理复杂问题中的重要作用
2018-12-07北京张祖志高祥旭
北京 张祖志 高祥旭
理想化的物理模型既是物理学建立的基本思想方法,也是物理学在解决实际问题的重要途径和方法,这种方法的思维过程要求学生在分析实际问题中针对研究对象的条件、物理过程的特征,建立与之相适应的物理模型,通过模型思维进行推理。在解决一些比较复杂的运动过程问题中我们常希望把运动过程构建成匀速直线运动和匀变速直线运动等运动过程模型,但却忽略了一个复杂的运动过程有时候也可以构建成一个直线运动与一个圆周运动的过程模型。
【问题】根据牛顿力学经典理论,只要物体的初始条件和受力情况确定,就可以预知物体此后的运动情况。
(1)如图1 所示,空间存在水平方向的匀强磁场(垂直纸面向里),磁感应强度大小为B,一质量为m、电荷量为+q的带电粒子在磁场中做匀速圆周运动,经过M点时速度的大小为v,方向水平向左。不计粒子所受重力。求粒子做匀速圆周运动的半径r和周期T。
(2)如图2 所示,空间存在竖直向下的匀强电场和水平的匀强磁场(垂直纸面向里),电场强度大小为E,磁感应强度大小为B。一质量为m、电荷量为+q的带电粒子在电磁场中运动,不计粒子所受重力。
a.若该带电粒子在电磁场中做水平向右的匀速直线运动,求该粒子速度v′的大小;
b.若该粒子在M点由静止释放,其运动将比较复杂。为了研究该粒子的运动,可以应用运动的合成与分解的方法,将它为0 的初速度分解为大小相等的水平向左和水平向右的速度。求粒子沿电场方向运动的最大距离ym和运动过程中的最大速率vm。

图1 图2
【品析】这是一道带电粒子在复合场中运动的综合问题,从力和运动关系入手,运用牛顿第二定律、平衡条件和构建理想化模型等综合考查学生分析问题、解决问题、构建模型和知识迁移的能力。整体来说因为有问题(1)和问题(2)中的a的铺垫,对于学生来说没有太大难度,但如果没有前面的铺垫,那么对于问题(2)中的b,学生往往会因为运动过程中的轨迹是曲线,受到的洛伦兹力大小和方向时刻变化的受力特点,对题目无从下手。现根据题目中的提示给出该题的分析过程,如图3所示。
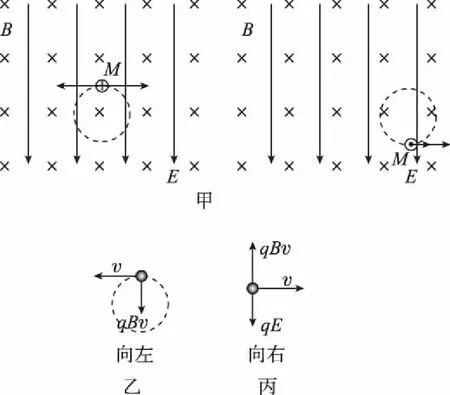
图3

如果这道题问题(2)中的b没有提示,那么这道题就是一个很好的竞赛题,对学生构建情境模型能力提出了更高的要求。
【解析】(1)根据牛顿第二定律洛伦兹力用来提供圆周运动的向心力有
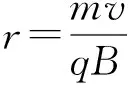
根据圆周运动周期公式


【策略】①在学习运动的合成与分解时,千万不要让学生以为一个复杂的运动只能分解成两个简单的直线运动;②要把数学中的“添加辅助线”的思想应用到物理问题的解决过程中;③分析研究对象的受力情况和运动过程,对比熟悉的运动过程模型的受力特点和运动特点,构建新的运动过程模型;④根据新的运动过程模型列出方程求解。
【应用】
1.一个质量为m的带正电小球,带电荷量为q,在匀强电场中运动,电场方向水平向右,场强大小为E。如图4所示,某时刻粒子经过a点,速度方向与电场线成60°角,经过时间t,它恰好经过b点,速度方向与电场线成30°角,试求:带电小球经过a点处的速度和从a到b的位移。
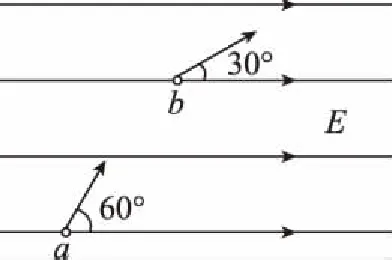
图4
【解析】如图5所示带电小球受竖直向下的重力mg和水平向右的电场力qE,根据受力特点,可以把带电小球的运动分解为水平方向的匀加速直线运动,竖直方向的匀减速直线运动。设带电小球经过a点处的速度大小为v0,则

图5


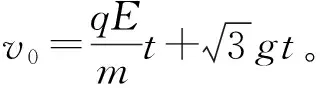
【点评】带电小球在重力和电场力的作用下,做匀变速曲线运动,当建立坐标轴后,把带电小球的运动分解为x轴方向的匀加速直线运动和y轴方向的匀减速直线运动。学生对于匀变速运动过程模型的问题求解还是非常熟悉的,所以处理起来并不困难。
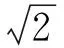

图6
(1)粒子在而后的运动过程中,速度方向与电场线方向垂直时的速度大小;
(2)粒子在而后的运动过程中,速度方向与电场线方向平行时的速度大小;
(3)a、b之间的距离。
【解析】粒子在电场力和洛伦兹力的作用下做的是摆线运动,利用平行四边形定则把速度分解为匀速直线运动和匀速圆周运动的运动模型进行处理。
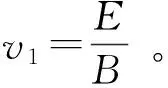
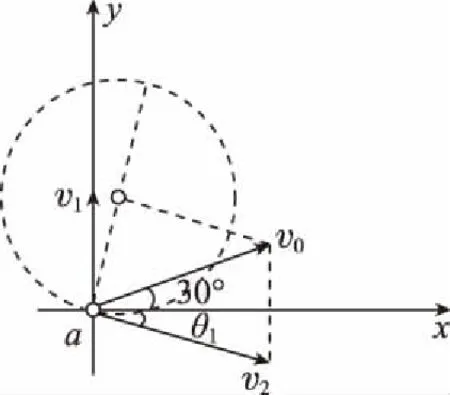
图7

图8
(1)粒子运动过程中只要v2方向与电场方向垂直,那么粒子的合速度一定与电场垂直,由此可知v1与v2同向或者反向。

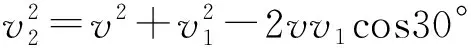

带电粒子速度与电场线垂直时满足如图9 所示情境
当v1和v2同向时(图9甲)得
当v1和v2反向时(图9乙)得

图9
(2)当带电粒子的速度与电场平行时,v1和v2满足关系如图10所示,由此可知两种情况下,速度大小相等,方向相反

图10
(3)如图11甲所示,粒子从a运动到b时
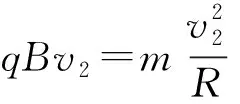
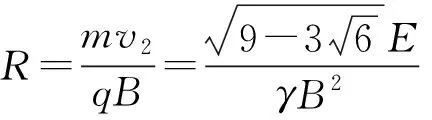
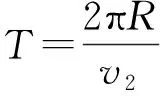

粒子由a运动到b时速度v2的偏转角为
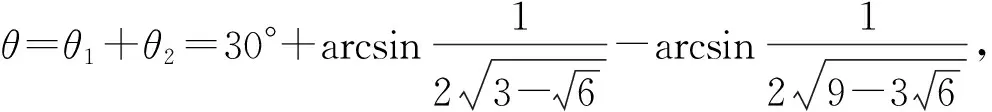
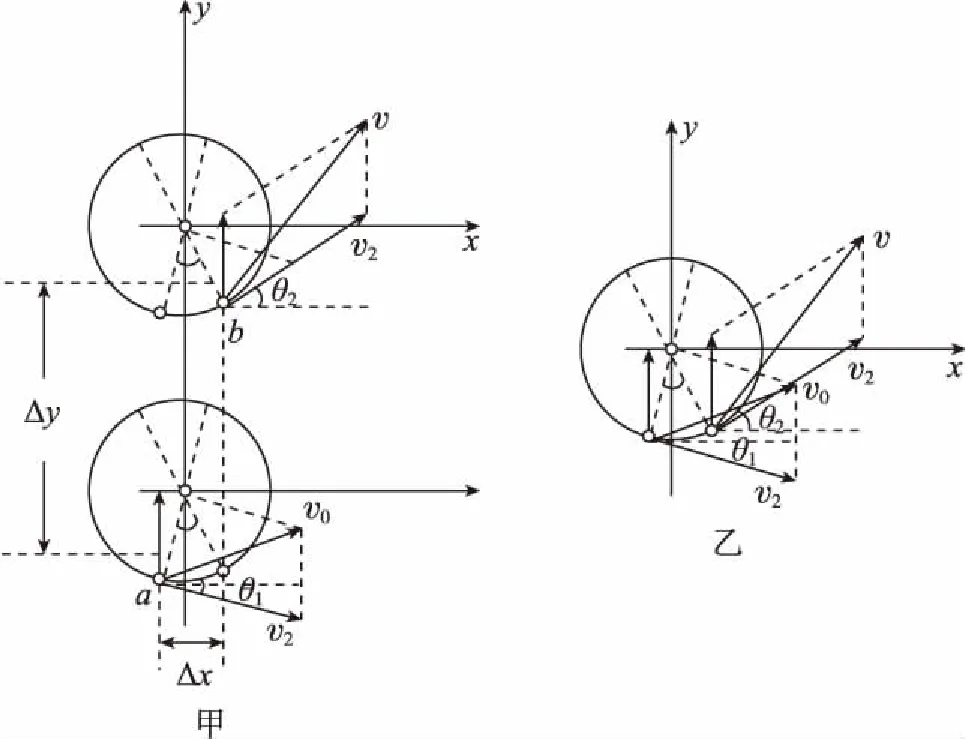
图11
竖直方向以v1做匀速直线运动位移的变化量y1满足
y1=v1t

以v2做匀速圆周运动引起的位移变化量y2满足
y2=Rcosθ1-Rcosθ2
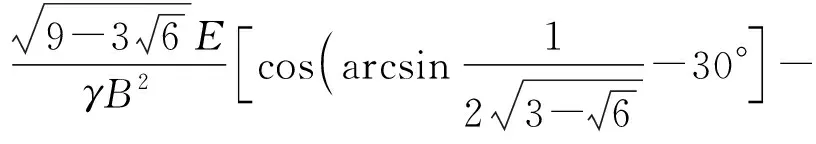
竖直方向总位移Δy=y1+y2
计算水平方向的位移时可以暂时忽略竖直方向的运动,因此带电粒子的圆周运动如图11乙所示
Δx=Rsinθ1+Rsinθ2



