分类例析天体运动中的追及与几何条件问题
2018-12-07河北牛红标
河北 牛红标
天体的运动问题一直是历年高考的热点问题,随着我国航天事业的快速发展,有关卫星的实际应用问题也逐渐成为高考命题的立足点,切合新课标下考查学生学以致用的实践能力,考查学生的核心素养,而这类相关问题分析较为复杂,尤其需要一定的形象思维能力,并能够画出相对应条件下的物理情景才能顺利解决。笔者对这些问题做了相关的整理,并给出相关的解题方法及技巧,希望能对学生有帮助。
一、追及相遇问题
【例1】被人们称之为“笔尖下的行星”的海王星的发现过程,给万有引力定律确立了正确坚实的地位。如图1所示,在长期观察过程中发现天王星A的行为总有些“古怪”,根据万有引力定律计算的结果总有一些偏差,天王星A周期性地每隔t0时间发生一次最大的轨道偏离,天文学家认为形成这种现象的原因可能在天王星外面还有一颗未发现的行星B,它的吸引使天王星的轨道发生了偏离。假设其运行轨道与A在同一平面内,且与A的绕行方向相同,它对A的万有引力引起A轨道的偏离。已知天王星的运动周期为T0,其轨道半径为R0,根据上述现象及假设,行星的运行轨道看作是圆形轨道,你能对未知行星B的运动得到哪些定量的预测?

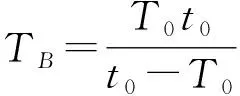
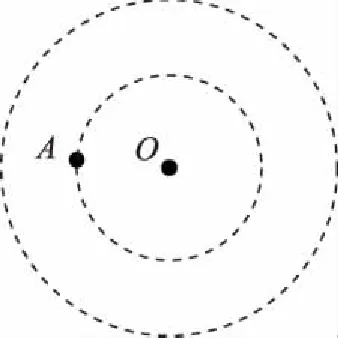
图1
可见加速度为定值,导体棒做匀加速直线运动。
可解得未知天体B的轨道半径
【例2】太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动,当地球恰好运行到某个行星和太阳之间,且三者几乎成一条直线的现象,天文学称为“行星冲日”。据报道,2014年各行星冲日时间分别是1月6日木星冲日;4月9日火星冲日;6月11日土星冲日;8月29日海王星冲日;10月8日天王星冲日,已知地球轨道以外的行星绕太阳运动的轨道半径如表所示,则下列判断正确的是

( )
A.地外行星每年都会出现冲日现象
B.在2015年内一定会出现木星冲日
C.天王星相邻两次的冲日的时间是土星的一半
D.地外行星中,海王星相邻两次冲日间隔时间最短
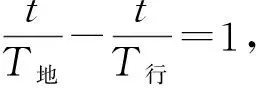
【点评】圆周运动不同轨道上卫星的追及问题中,距离最近,距离最远通常是要求理解的两个重要问题,注意转过的角度与圈数的关系,结合实际情境是解决问题的关键。
二、在赤道上观测卫星问题

( )
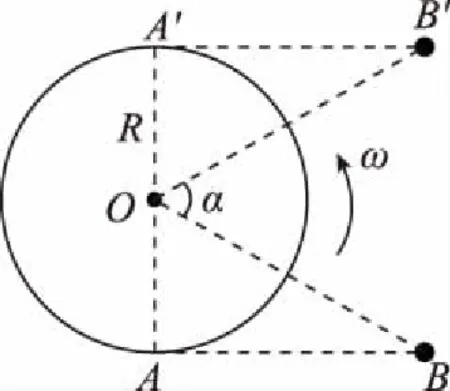
图2

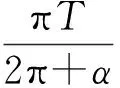


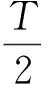
【例4】地面卫星监测技术在军事、工业、农业、生产、生活等方面发挥着巨大作用,对地面上的重要目标需要卫星不间断的进行跟踪监测是一项重要任务。假设在赤道上有一个需跟踪监测的目标,其中一颗监测卫星,位于赤道平面内,离地面的飞行高度为R,飞行方向与地球自转方向相同,设地球的自转周期为T,地球半径为R,地球表面的重力加速度为g,忽略大气层对光线传播的影响,则此卫星在一个运动周期中对目标连续监测的最长时间为
( )
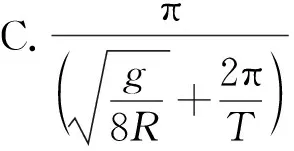
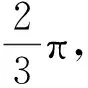

图3
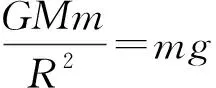
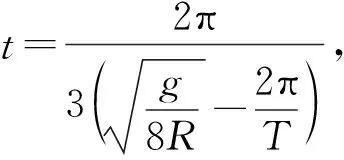
故本题的正确选项为A。
【点评】这两个例题涉及不同转速的两个物体的追及问题和光的直线传播问题,相对难度较大,恰好不能观测到时对应位置与地球对应点相切,作出并理解两个关键位置的示意图,并根据示意图找出对应的几何关系,再根据转动追及相关知识求解。
三、卫星与地面通信问题
【例5】有一颗同步卫星,其定点位置与东经98°的经线在同一平面内,在甘肃省嘉峪关处设有微波接收站,用来接收卫星发送的微波信号,嘉峪关处的经度和纬度近似取为东经98°和北纬α=40°,已知地球半径R、地球自转周期T、地球表面重力加速度g(视为常量)和光速c,微波信号看作沿直线传播,则有关同步卫星以下说法正确的是
( )
A.同步卫星可以定点在嘉峪关的正上方
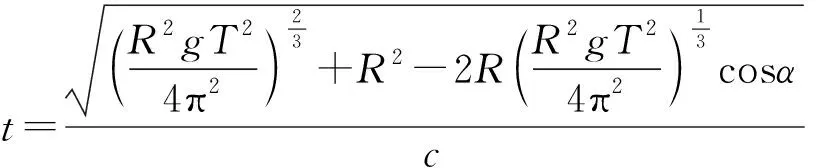
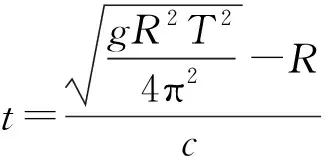
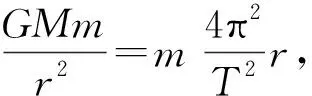
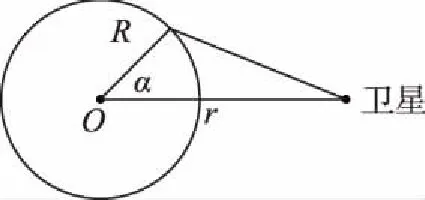
图4
对上面几式联立可解得
所以C正确,D错误。本题的正确选项为C。
【例6】“嫦娥一号”探月卫星是在绕月极地轨道上运动的,加上月球的自转,因而“嫦娥一号”卫星能探测到整个月球的表面。12月11日“嫦娥一号”卫星CCD相机已对月球背面进行成像探测,并获取了月球背面部分区域的影像图。卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地球运动的公转半径为R0,月球绕地公转的周期为TE,地球半径为RE,月球半径为RM。当“嫦娥一号”卫星绕月极地轨道的平面与月球绕地公转的轨道平面垂直,也与地心到月心的连线垂直时(如图5所示)探月卫星向地球发送所拍摄的照片,(已知光速为c)以下说法正确的是
( )

图5
A.在地球上一半的范围内能收到发送的照片信息
C.地球上赤道上的某个位置最先收到照片信息
【解析】由于卫星发送的信号是由一个点发出的,所以地球上接收到信息的区域小于一半;设卫星质量是m,月球和地球的质量分别为M月和M地。卫星绕月球做圆周运动,由月球的万有引力提供卫星的向心力,由牛顿第二定律可得

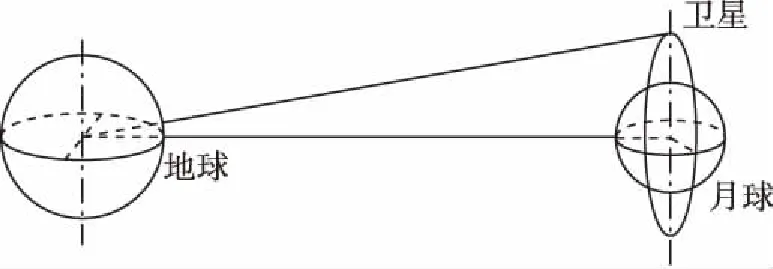
图6
设探月极地轨道上卫星到地心的距离为L0
则卫星到地面最短距离为L0-RE
将照片发回地面的时间
D正确,C错误,故本题正确选项为D。
【点评】本题解题关键是照片由卫星传送到地球上的哪一点时间最短,即卫星到地面上的最小距离,由几何关系可以证明,当沿着卫星与地心连线方向传送时距离最小,历时最短。
四、天体遮挡问题
【例7】某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,试问,春分那天(太阳光直射赤道)在日落12小时内有多长时间该观察者看不见此卫星?已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对光的折射。
【解析】由题意作出卫星环绕地球运动的情景图,当卫星进入地球的阴影区的S点时,太阳光被遮挡,无法看到此卫星,当运动到离开阴影区域时重新被观察到,由图7可知卫星在转动角度为2θ的时间内看不到此卫星,设卫星的轨道半径为r
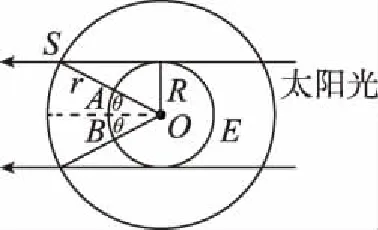
图7
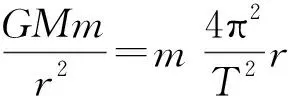
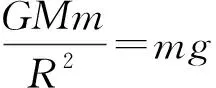
【例8】我国发射的“嫦娥一号”探月卫星沿近似于圆形的轨道绕月飞行。为了获得月球表面全貌的信息,让卫星轨道平面缓慢变化。卫星将获得的信息持续用微波信号发回地球。设地球和月球的质量分别为M和m,地球和月球的半径分别为R和R1,月球绕地球的轨道半径和卫星绕月球的轨道半径分别为r和r1,月球绕地球转动的周期为T。假定在卫星绕月运行的一个周期内卫星轨道平面与地月连心线共面,求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(用M、m、R、R1、r、r1和T表示,忽略月球绕地球转动对遮挡时间的影响)。
【解析】如图8所示,O和O′分别表示地球和月球的中心。在卫星轨道平面上,A是地月连心线OO′与地月球面的公切线ACD的交点,D、C和B分别是该公切线与地球表面、月球表面和卫星圆轨道的交点,根据对称性,过A点在另一侧作地月球面的公切线,交卫星轨道于E点。卫星在圆弧BE上运动时发出的信号被遮挡。
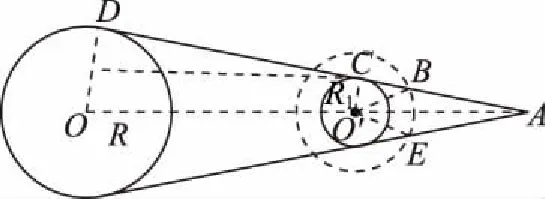
图8
设探月卫星的质量为m0,万有引力常量为G,根据万有引力定律有
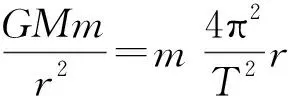

式中T1是探月卫星绕月球转动的周期

设卫星的微波信号被遮挡的时间为t,则由于卫星绕月球做匀速圆周运动,有
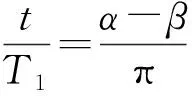
式中,α=∠CO′A,β=∠CO′B。
由几何关系得
rcosα=R-R1⑤
r1cosβ=R1⑥
由③④⑤⑥式得
【例9】A、B是两颗人造地球卫星,绕地球做匀速圆周运动,轨道在同一平面内,绕行方向相同,其运动周期分别为T1和T2,并且A的轨道半径小于B,A距地面高度为h1,B距地面高度为h2;当两颗卫星位置的连线与地面相切时,如图9所示,O为地心,两颗卫星与地心的连线与两卫星连线间的夹角分别为α、β,地球半径为R,若A、B两卫星的信息通讯的微波以直线传播,且忽略大气层的影响,由于地球的遮挡,一段时间t内两卫星不能直接进行联系,关于两颗卫星的以下说法正确的是
( )
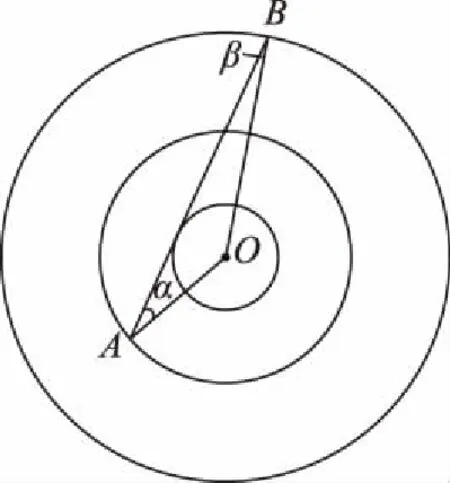
图9


图10
【点评】本题难度较大,两个卫星在以不同的角速度运动,相对位置不断发生变化,尤其是CD选项的分析,选B卫星作为参考系,画出相应的遮挡位置,运用转动追及的相关知识解决问题。
五、观测范围问题
【例10】侦察卫星在通过地球两极上空的圆形轨道上运动,它的运动轨道距离地面的高度为h,要使卫星在一天时间内将地面上赤道各处在日照条件下的情况全部都拍摄下来,卫星在通过赤道上空时,卫星的摄像机至少能拍摄地面上赤道圆弧的弧长是多少?设地球的半径为R,地面处的重力加速度为g,地球自转周期为T。
【解析】情景如图11所示,

图11
由题意知卫星需要在日照条件下每次经过赤道上方时进行拍照,设卫星运动周期为T1,则

则在卫星运动一个周期内地球转过的弧长s=θR=ωRT1

【点评】注意本题中的条件,要求卫星在日照条件下拍摄,所以卫星每运动一个周期只能拍下一张,相对应地球转过的弧长。

