并网逆变器小信号建模方法对比及其适用性分析

2018-12-06张昌华陈树恒刘群英

电力系统自动化 2018年23期

刘倪, 张昌华, 段雪, 陈昕, 陈树恒, 刘群英

(1. 电子科技大学机械与电气工程学院, 四川省成都市 611731; 2. 重庆邮电大学自动化学院, 重庆市 400065)

0 引言

微电网作为一种将新能源、负荷、储能整合在一起以“良好公民”的形式并网的能源利用方式,受到了国内外专家学者的关注[1]。作为微电网中微电源并网发电的重要接口,逆变器凭借控制灵活、适应面广、成本相对低廉和使用方便等优点,得到了广泛应用[1-20]。由此带来了多逆变器互联运行[2-3]、控制器设计[4-7]、微电网稳定性分析[8-19]等一系列问题。其中,小信号模型在逆变器控制器参数选取、微电网阻尼分析中得到了广泛应用,本文对此予以研究。

目前,微电网小信号稳定性分析的建模方法大体上分为两类。一类为考虑逆变器中LC/LCL滤波器、所连线路与负载的动态特性的小信号模型。本文将其称为高阶模型[8-13]。文献[8]对采用虚拟同步发电机(virtual synchronous generator,VSG)控制策略的微电源,建立了高达20阶单VSG小信号模型,通过参数灵敏度的计算,分析了控制参数、线路参数对特征根的影响规律。文献[9]对包含3个发电节点、2个负荷节点的微电网,建立了高达47阶的小信号模型,并将该模型获取的特征根分为低频特征根、中频特征根和高频特征根,分析了下垂系数和电路参数对微电网稳定性的影响。文献[10-11]利用类似方法,对包含不同逆变器控制策略的微电网小信号稳定性分析展开讨论。文献[12-13]分别利用高阶模型研究了同步频率谐振和谐波谐振问题,提出了引入虚拟阻抗来抑制谐振的方法。虽然这些高阶模型较为准确地描述了系统的动态特性,但在阻尼分析、控制器参数设计上,高阶模型提供的高频且快速衰减的振荡模态往往影响甚微,同时还增加了分析与设计的复杂程度。

而另一类小信号模型忽略了滤波器与线路的动态特性,因此所获得的小信号模型阶数显著低于高阶模型。本文将这类模型称为降阶模型[4,15-20]。文献[4]将采用VSG控制策略的单逆变器系统降阶为二阶典型系统,分析了低频振荡发生机理,指出逆变器惯性参数和阻尼系数分别决定振荡模式频率与衰减速度。文献[15-16]将逆变器等效为电压源,建立考虑控制器动态特性的双机系统小信号模型,在此基础上分析了虚拟转动惯量、下垂参数和电路参数与微电网稳定性的关系。文献[17]提出基于极坐标的小信号建模方法。文献[18]建立了VSG工频小信号模型,并用频域分析的方法研究有功环和无功环的参数设计问题。上述文献都没有对降阶模型中的降阶方法对所获系统特征根精度、模型意义及应用场合的影响进行分析。同时也没有文献对近年来出现的鲁棒下垂控制策略的小信号建模开展研究。

基于此,本文以具有鲁棒下垂控制的VSG为例,对小信号模型建模方法及其特征根的精度、小信号模型意义及应用场合进行对比研究。针对单逆变器并网系统,先建立其高阶小信号模型,然后将其化简为降阶模型,并获得特征根的误差表达式。通过搭建MATLAB/Simulink仿真模型,验证了两种小信号模型的准确性。随后,对两种模型所捕获低频特征根的精度进行分析。最后,利用参数灵敏度与根轨迹分析了两种模型在不同场景的应用效果,结合功率响应波形验证了这些结论的正确性。

1 单逆变器控制策略及小信号模型

1.1 逆变器系统及接口电路模型

微电网常有并网和孤岛两种工作模式[1]。当其工作在并网模式时,并网点可以视作一个无穷大母线,此时系统可以等效为一个单机无穷大模型。当其工作在孤岛模式时,微电网通常由多个微电源、负载、储能装置组成,此时可以将除所研究微电源及其线路之外的电路等效为一个可调电压源。这两种情况下,当研究微电源自身的控制策略时,均可用图1所示的单逆变器并网系统来表示。该系统主要包括微电源及储能装置、三相桥式逆变电路、LC滤波器、输电线路和控制器。

图1 单逆变器并网系统Fig.1 Single-inverter grid-connected system

图1中Lf与Ra为逆变器的滤波器滤波电感及电阻;Cf为滤波电容;RE与LE为逆变器连接到公共耦合点(point of common coupling,PCC)的线路阻抗;et和i分别为逆变器输出电压与输出电流;U与φ分别为逆变器的脉宽调制(pulse width modulation,PWM)驱动信号的幅值与相位;Et与θ分别为端电压的幅值与相位;Vpcc与α分别为网侧PCC处的电压幅值与相位。

1.2 LC滤波器与线路阻抗模型及其线性化

根据图1可得描述LC滤波器及线路阻抗的动态特性的方程如下[10]:

(1)

式中:ω为逆变器角频率,udq,edq,vpcc,dq分别为逆变器的调制波u、端电压et和PCC处电压vpcc分解到以逆变器控制器ω-φ为参考频率和相位的旋转坐标系下的dq轴分量;il,dq和idq分别为流过LC滤波器电感的电流il与流过线路电流i的dq轴分量;udq=[ud,uq],eqd=[eq,ed],并且后文下标为dq的均为此类含义。

将式(1)线性化,得到小信号模型见式(2)[9]。

BLCL2Δvpcc,dq+BLCL3Δω

(2)

Δx1=[Δil,dqΔedqΔidq]T

(3)

式中:矩阵ALCL,BLCL1,BLCL2,BLCL3见附录A式(A1)。

1.3 鲁棒下垂控制的VSG及其线性化

本文将虚拟转动惯量引入鲁棒下垂控制中,得到具有鲁棒下垂控制的VSG,如图2所示[3,6]。该控制策略可以更好地做到多逆变器之间有功和无功功率的均匀分配。同目前大部分VSG研究一样,控制器的参数选取及其对系统稳定性的影响是其研究重点。值得说明的是,包括本文讨论的鲁棒下垂控制的VSG在内,大多数VSG都可通过Phillips-Heffron模型与同步发电机(synchronous generator,SG)等效[16,21-23],故本文讨论的方法与结论对包含其他形式VSG逆变器的微电网小信号稳定性建模与分析也有借鉴意义。

图2 鲁棒下垂控制的VSGFig.2 VSG with robust droop control

图2中:系数m和n为感性输出阻抗的逆变器下垂控制系数;系数Ke和J分别为端电压反馈系数与虚拟转动惯量;P*,Q*,E*,ω*分别为给定有功功率、无功功率、端电压幅值和额定频率;ωc为低通滤波器截止频率。

通过瞬时功率理论计算得到低通滤波环节的输入p和q及幅值Et,则经低通滤波器后可表示为:

(4)

为简化分析,本文将微电源及储能装置等效为理想电压源,并且忽略三相桥式逆变电路的动态过程[8]。根据图2中的控制策略,得到逆变器有功功率—频率调节、无功功率—电压调节方程如下:

(5)

式中:ωn为额定角频率。

将式(4)和式(5)线性化,得到式(6)所示的小信号模型。

(6)

Δx2=[ΔδΔωΔPΔQΔuqΔEt]T

(7)

式中:矩阵Ap,Bp,Ccw,Ccv见附录A式(A2)。

1.4 PCC的母线模型及其线性化

单逆变器并网模型中选择逆变器本身ω-φ旋转坐标系为公共的DQ坐标系。故设PCC的电压相位与公共DQ坐标系的Q轴存在δB的相位差,则PCC处电压以及功角表示为:

(8)

式中:ωg为公共耦合点电压的角频率。

将式(8)线性化,得到小信号模型为:

(9)

式中:矩阵Bg,Bbus,Bpcc,Cpcc见附录A式(A3)。

1.5 单逆变器并网小信号模型

将单逆变器并网模型中公共DQ坐标系作为逆变器本身的旋转坐标系,合并式(2)、式(7)、式(9)可得鲁棒下垂控制VSG并网的13阶小信号模型如式(10)所示。

(10)

(11)

Δxsys=[Δx1Δx2ΔδB]

(12)

式中:矩阵Bg,h和Bpcc,h的具体表达式见附录A式(A4)。

2 单逆变器并网模型的降阶

通过对高阶小信号模型进行分析可以发现,影响单逆变器并网系统动态特性的状态变量有3种:分别为与线路相关的状态变量Δx1、与控制策略相关的状态变量Δx2、与公共耦合点母线相关的状态变量Δx3。文献[24]指出上述3个状态在动态过程中的衰减速度不同,其中Δx1衰减较快,而Δx2及Δx3衰减速度较慢。故可通过分离Δx1与Δx2和Δx3,实现对高阶模型的降阶。

根据式(10)可知,高阶模型中状态变量Δx1可表示为:

Δx1=(sI-ALCL)-1(BLCL1Ccv+BLCL3Ccw)Δx2+

(sI-ALCL)-1BLCL2BpccΔδB

(13)

式中：I为单位矩阵。

若忽略快速衰减的变量Δx1的动态过程,即将其动态模型替换为稳态模型,可令s=0。同时考虑到稳态模型中电抗ωL取为ωnL,则BLCL3为零矩阵。故可将式(13)重写为:

Δx1=(-ALCL)-1(BLCL1CcvΔx2+BLCL2BpccΔδB)

(14)

利用式(14)消去式(10)中与状态变量Δx1的相关状态,则可获得鲁棒下垂控制VSG并网的7阶小信号模型如式(15)所示。

(15)

(16)

式中:矩阵Bg,l和Bpcc,l的具体表达式见附录A式(A5)。

3 两种模型低频特征根误差分析

3.1 高阶模型中低频特征根计算

微电网稳定性研究普遍关注小信号模型的特征根。降阶模型的特征根与其在高阶模型对应特征根的误差之和值得分析。但因高阶中的Asys,h和降阶中的Asys,l阶数不同,需先将Asys,h变换为7阶矩阵。为此,将式(13)代入式(10)中消去状态变量Δx1,可得:

(17)

其中:

(18)

由文献[25]可知,式(17)的特征根必定是式(10)的特征根。故可以将式(15)与式(17)之间的误差视为高阶模型和降阶模型之间的误差。但值得注意的是,在消去Δx1的同时,上述变换也消去了原高阶模型中的6个中高频特征根。由于仅对降阶模型中存在的特征根进行分析,故此处变换不影响分析结果。

3.2 误差表达式

将高阶模型中矩阵Asys,he分解为两部分:一部分为降阶模型Asys,l,一部分代表对矩阵Asys,l的摄动,即高阶模型与降阶模型的误差,则有

Asys,he(s)=Adelta(s)+Asys,l

(19)

其中Adelta(s)的表达式如式(20)所示。

(20)

由矩阵摄动理论可知,系统特征根的近似解为:

(21)

式中:Ψi和Φi分别为高阶模型中特征根λi相关联左、右特征向量。

若忽略摄动矩阵变化对特征向量的影响,则对于特征根λi,高阶模型与降阶模型之间的误差可以定义为:

(22)

根据上式可知,Adelta可以反映降阶模型与高阶模型之间每一个特征根的误差评估,并从Adelta的表达式看出这种误差主要与系统初始状态、线路与滤波器参数有关。

两种模型之间所有特征根误差可用误差向量Δλ表示。在欧氏空间中,常使用向量的2-范数对向量进行量度,反映向量的长度。故可将两个模型低频特征根的误差定义为:低频特征根误差之和等于‖Δλ‖2。

4 降阶小信号模型的精度分析

4.1 小信号模型准确性的验证

为了验证本文推导的小信号模型的正确性,在MATLAB/Simulink中搭建单逆变器并网系统的仿真模型和式(10)、式(22)所示的小信号模型,分别表示系统非线性模型、高阶线性模型和降阶线性模型。系统拓扑见图1。参数选择为微电网常规参数[26-27],见附录A表A1。

在系统运行到2 s时,给网侧电压增加-0.02(标幺值)的阶跃扰动。系统非线性模型、高阶线性模型、降阶线性模型在该扰动下的动态响应曲线如图3所示。

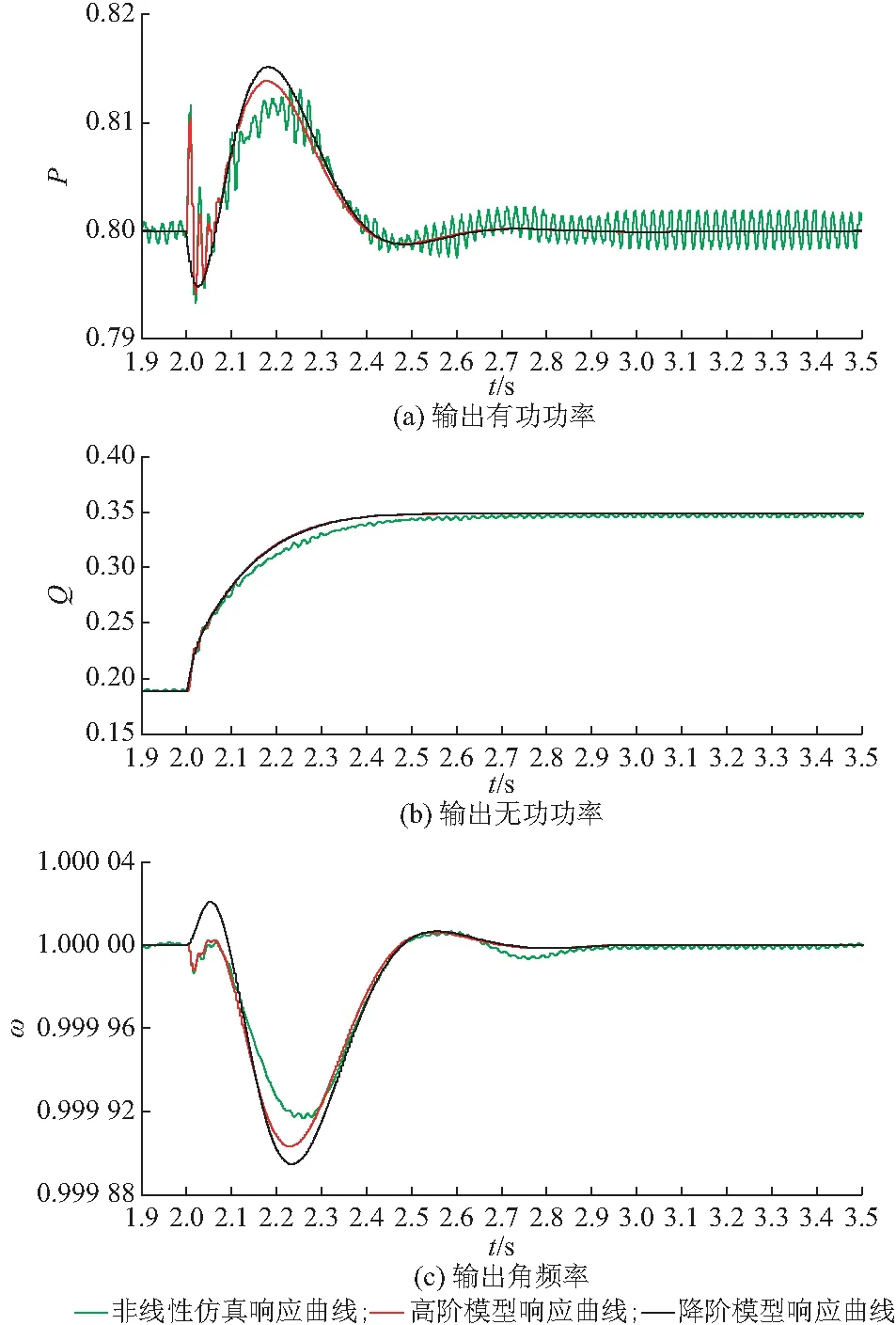
图3 两种小信号模型与非线性模型仿真结果对比Fig.3 Comparison of simulation results between two small-signal models and nonlinear model

图3中(a)至(c)分别表示系统输出有功功率、无功功率与角频率。通过观察可以发现,针对同一状态变量,3种模型输出的响应曲线基本重合,且高阶模型与降阶模型皆可捕获系统的低频分量,但降阶模型中无高频分量。这表明,对于单逆变器并网系统,无论是高阶模型还是降阶模型,均能较好地描述系统扰动后动态过程的低频部分。

4.2 两种模型的特征根及误差分析

针对图1的单逆变器并网系统,通过求解非线性方程或者MATLAB/Simulink仿真得到系统的初始状态。将相同的初始状态及系统参数代入小信号模型中,通过式(10)的Asys,h和式(15)的Asys,l可以求解两种模型下的系统特征根与参与因子。系统参数与初始状态分别见附录A表A1与表A2。

任取一组特征根,通过计算参与因子,得到影响每一个特征根的主要相关状态变量,如表1所示。由表1可知,两种模型都包含一个零根λ7,其原因为该系统的公共坐标系为逆变器自身的旋转坐标系。同时,根据文献[9]的划分方法可以按其对应的振荡频率,高阶模型的特征根可分为高频、中频、低频3种特征根。其中,λ1至λ6为低频特征根,λ8和λ9为中频特征根,λ10至λ13为高频特征根。并且由表1可知,根据参与因子,状态变量Δx1与中高频特征根λ8至λ13相关,状态变量Δx2与低频特征根相关。这与3.2节对Adelta的讨论结论一致。

表1 单逆变器并网系统中两种小信号模型的特征根比较Table 1 Comparison of eigenvalues between two small-signal models in a single-inverter grid-connected system

传统电力系统小信号稳定性分析中通常关注的频率为0.1～0.3 Hz的区域振荡和0.7～2.0 Hz左右及以上的局部振荡模式[21]。由于鲁棒下垂控制的VSG中引入同步发电机的转子方程,微电网中也可能引入上述频率的功率振荡。从表1可见,两种模型均捕获了1.87 Hz的低频振荡频率,并且两种模型获取的低频特征根误差极小。

由式(22)可知:低频特征根的误差主要与系统初始状态及线路阻抗相关。为此,本文分别就系统不同初始状态和不同阻抗比下,两种小信号模型获取的低频特征根的精度进行分析。在鲁棒下垂控制的VSG中,在频率固定时,逆变器端电压的幅值可以代表系统的不同的初始状态[27]。由于电网规定电压波动应在±10%以内,故只对逆变器端电压处于0.9～1.1(标幺值)之间的状态进行讨论。根据式(22),图4分别绘制逆变器端电压从0.9变化至1.1和阻抗比从0变化至50,两种模型获取的低频特征根的误差2-范数的变化轨迹。从图中可以发现:针对所给系统,无论是初始状态不同还是阻抗比不同,两个模型获取的低频特征根的误差都比较小。换言之,降阶模型通过忽略中高频特征根和损失些微的低频特征根精度,换来了系统模型的明显降阶。

5 两种小信号模型的适用场景分析

5.1 基于灵敏度和根轨迹的模型适用性分析

逆变器的小信号模型常用于并网逆变器的参数整定及稳定性分析[18]。通过求解参数灵敏度[8],可以考查系统某一参数变化引起的特征根的变化情况,从而实现两种建模方法的应用场合的比较。不同参数下,通过模型获得的根轨迹及功率响应波形可以验证分析结论的正确性。

图4 两种小信号模型的特征根误差变化轨迹Fig.4 Trajectories of eigenvalue errors for two small-signal models

限于篇幅,本文仅计算控制器参数m和Ke与线路参数RE和LE对不同特征根的灵敏度,计算结果如附录A表A3所示。通过观察可以发现:参数m主要影响两种模型的特征根λ1，λ2，λ4,并使λ4向左移动,λ1和λ2的实部向右移动,系统稳定性有所下降;参数Ke主要影响两种模型的特征根λ3和λ5,并使λ5向左移动,λ3向右移动,系统稳定性有所下降。且在高阶模型中,m和Ke对高频特征根的灵敏度为0。这意味着,控制器参数m和Ke对系统高频特征根没有影响。同时,无论高阶还是降阶模型,控制器参数对特征根的影响效果一致。因此,若研究控制器参数整定问题时,采用降阶模型是足够的。

与控制参数相似,无论高阶还是降阶模型,线路参数LE和RE等对低频特征根的影响效果也是一致的。且当阻抗比(RE/LE)增大时,特征根λ3向右移动,系统失去稳定性。同时,在高阶模型中,线路参数RE和LE还影响中高频特征根。且参数LE使λ8至λ13快速向右移动,系统稳定性降低;参数RE使λ8至λ13快速向左移动,系统稳定性增强。这意味着,阻抗比较低时,系统高频特征根的实部将接近虚轴,并产生较高频率的功率振荡。比如,表1中特征根λ8和λ9表明系统将产生频率为50 Hz的功率振荡。这表明,在研究系统次同步与高频振荡时,应采用高阶模型,且感性网络更容易发生中高频失稳的可能性。

进一步,本文使用根轨迹的方法对上述结论进行说明。图5(a)至(c)给出了下垂系数m、端电压反馈系数Ke和线路阻抗比增大时,两种模型的系统特征根变化轨迹。放大图5(c)中低频特征根区域得到图5(d)。由图可知,3种情况下,无论高阶模型和降阶模型,低频特征根的运动轨迹变化一致。其中,图5(a)表明,参数m使λ4向左移动,λ1和λ2的实部向右移动,直至m增大到0.09时,两个模型所获的特征根λ1和λ2向右穿越虚轴,系统失稳。图5(b)表明,参数Ke使λ5向左移动,λ3向右移动,直至Ke增大到5时,两个模型所获的特征根λ3接近虚轴,系统接近失稳。图5(c)和(d)表明,阻抗比RE/LE使λ1，λ2，λ8至λ13向左移动,λ3和λ4的实部向右移动,直至RE/LE增大到34时,两个模型所获的特征根λ3向右穿越虚轴,系统失稳。同时注意到,图5(c)中,阻抗较小时,系统中高频特征根λ8至λ13的实部都接近为0,系统接近失稳。这意味着,针对低阻抗比或感性线路,系统有可能发生中高频失稳的可能性,使用降阶模型无法确定系统的稳定状态。这与附录A表A3灵敏度分析所获结论一致。

5.2 仿真分析

为了进一步验证5.1节的结论,将4.2节算例中有功下垂系数增加至0.1和将阻抗比降低至0,有功功率响应波形如图5(e)和(f)所示。由图可知,有功下垂系数取值为0.1时,两种模型都能反映系统失稳,且振荡频率在5.5 Hz左右。但当线路阻抗比取值为0时,降阶模型的功率响应波形表明系统处于稳定状态,而高阶模型的功率响应波形表明系统失稳,且以50 HZ的频率振荡。这意味着,系统失稳是由降阶模型无法捕获的中频特征根λ8和λ9导致的。这些事实都表明,降阶模型可以应用于控制器参数的整定,但也有可能漏掉系统中高频失稳的情况,尤其是在感性网络中。