大规模光伏并网对区域互联系统机电振荡影响分析

程青青， 都洪基

(南京理工大学 自动化学院，江苏 南京 210094)

0 引 言

近年来随着光伏相关技术的发展，光伏渗透率一直保持着快速增长，相应地，光伏并网对系统稳定性的影响也日益显著，因此针对高渗透率光伏并网系统的安全稳定性问题不容忽视[1,2]。

机电振荡又名低频振荡或者功率振荡，当系统中发生小扰动时，发电机转子间会产生频率为0.1～2.5 Hz的相对摇摆。根据参与机组的不同，低频振荡可以分为局域振荡和区间振荡，通常，前者的频率在0.1～1.0 Hz之间，而后者频率则在1.0～2.5 Hz之间[3]。电力系统发展至今，其低频振荡问题一直备受关注，特别是大型互联电网，由于缺乏足够的阻尼，极易发生低频振荡现象，从而严重影响系统的安全稳定运行[4]，由此可以看出，研究光伏接入对大型区域互联系统低频振荡特性的影响十分重要。

目前已有大量文献针对光伏并网对系统潮流以及暂态稳定性的影响进行了研究。文献[3]研究了4机两区域系统中大规模光伏接入对系统小信号稳定性的影响，分析结果表明其影响有正有负，与光伏并网点、并网容量等因素有关。文献[5]采用阻尼转矩法对光伏并网对系统机电振荡模式的影响进行了研究，仿真结果表明：随着光伏并网容量的增加，光伏并网可能提供正的阻尼转矩，也有可能提供负的阻尼转矩，但该文献采用的是单机无穷大系统，仅仅考虑了区域振荡，因此不能研究光伏并网对区域互联系统的影响。文献[6]对风光并网系统的低频振荡模式进行了研究，研究结果表明风光并网会增加系统的机电振荡模式，但并没有指出增加的模式是否与光伏相关。文献[7]同时采用了prony分析法和特征值分析法对光伏并网系统的阻尼特性进行了研究，结果表明随着光伏容量的提升，大部分机电振荡模式的阻尼比都不会受到影响，但振荡频率会随着增加。文献[8]研究了光伏接入对新英格兰系统区域间低频振荡模式的影响，结果表明随着光伏并网容量的增加，系统阻尼削弱。文献[9]系统潮流的变化是影响系统阻尼特性变化的重要因素，因此光伏并网对系统机电振荡的影响有利有弊。

基于以上分析可知，针对光伏并网系统低频振荡特性的研究，采用不同的算例或者不同的方法，所得到的结果也有所差异，其中文献[3]以4机系统为算例，从机理角度分析了光伏并网对系统低频振荡的影响，但其分析具有一定的局限性，其结论可能不适用于其它多机系统。为进一步从机理角度研究光伏并网系统对区域互联系统的影响，本文以8机36节点为例，在DIGSILENT/Power Factory软件中搭建相应的光伏并网系统模型，基于模式分析法对光伏并网系统的低频振荡特性进行分析，研究不同并网点、并网容量以及并网输送距离等因素对系统阻尼特性的影响。分析结果表明光伏并网点、并网容量等因素不同时，可能会增强系统阻尼，也可能导致其恶化。

1 光伏发电系统动态模型

在进行光伏接入系统分析之前，要先针对光伏电站进行建模。文献[10]详细研究了光伏发电系统的数学模型，推导出了一种适用于稳定性分析的动态模型。光伏建模主要包括光伏阵列、逆变器及其控制模块的建模。

光伏发电系统的电压电流特性表达式如下：

(1)

式中：Vpv和Ipv分别为光伏的电压和电流；Ns和Np分别表示串联和并联的光伏阵列的数量；n为理想化因子；k为波兹曼常数；Tj为光伏阵列的工作温度；q为电子电荷量；Ir表示太阳光照的强度；Isc和I0分别为短路电流和饱和电流。

图1为光伏两级式变换器模型。如图1所示，光伏发电系统通过两级变换器接入电网，其中DC/DC变换器主要实现光伏的最大功率控制。光伏电站机侧的DC/DC变换器和网侧的DC/AC变换器的控制策略分别如图2和图3所示。

图1 光伏两级式变换器模型

图2 机侧DC/DC控制策略框图

图3 网侧DC/AC控制策略框图

由图2可以得到如下一阶微分方程：

(2)

同时，可以得到光伏电站机侧电流表达式：

Ipv=KpP1(Ppvref-Ppv)+XP1

(3)

由图3可以得到DC/AC电压源变换器的二阶微分方程：

(4)

可得到光伏注入系统的电流表达式：

(5)

两级变换器之间的电容的电流和电压如下式所示：

(6)

以光伏电站母线电压定向，进行dq变换，可以得到光伏注入系统的有功和无功的表达式如下：

(7)

忽略有功损耗，可以得到电容处的电流如下：

(8)

根据光伏电池的电压、电流可得到其输出有功表达式：

Ppv=VpvIpv

(9)

基于式(1)～式(9)可以得到光伏并网的简化数学模型。

2 低频振荡模态分析

基于以上光伏动态建模，建立相应的含光伏电站的电力系统模型，假设光伏并网系统以式(10)所示的非线性系统描述。

(10)

式中：x表示系统n维状态变量。将式(10)在系统平衡点处进行泰勒展开，可得：

(11)

当发生小干扰故障时，系统可以近似为线性系统，系统线性化方程如下：

(12)

(13)

(14)

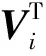
(15)

pki综合考虑了可观性uki和可控性vki，反映了模式i和第k个状态变量相互之间的参与程度。

机电回路相关比ρi度量了λi与发电机状态变量Δω和Δδ之间的相互参与程度，其表达式如下：

(16)

因此，判别λi是否为低频振荡模式的判据如下：

(17)

N机系统一般存在(N-1)个机电振荡模式。阻尼比大于10%的机电振荡模式为强阻尼模式，阻尼比小于3%则为弱阻尼模式，阻尼比小于0则表示负阻尼模式，研究中需要对弱阻尼和负阻尼模式进行重点关注。

3 算例分析

为分析大规模光伏并网对系统机电振荡状态的影响，本文以8机36节点系统为例，具体的发电机出力以及负荷分布参数详见参考文献[11]，通过合理调整部分线路参数，使系统成为两区域互联系统。在DIGSILENT/Power Factory上搭建相应的仿真模型进行仿真分析。系统单线图如图4所示。

图4 8机36节点系统单线图

采用本文所叙述的方法对系统进行模态分析，如表1所示，该系统共有7个机电振荡模式。根据阻尼频率可以看出，模式1～3为局域振荡，而模式4～7为区间振荡。

表1 模态分析结果

各机组对各模式的参与因子如表2所示。由表2可知，模式1表现为G2和G4之间的局域振荡，模式2为G3和G4之间的局域振荡，模式3为G1、G3之间的局域振荡，模式4为G1和G7之前的区间振荡，模式5为G1、G3以及G8之间的区间振荡，模式6为G1、G2、G3和G7、G8之间的区间振荡，模式7为G1、G3、G7之间的区间振荡。其中G1、G2、G3、G4、G5为区域1，G7、G8为区域2。

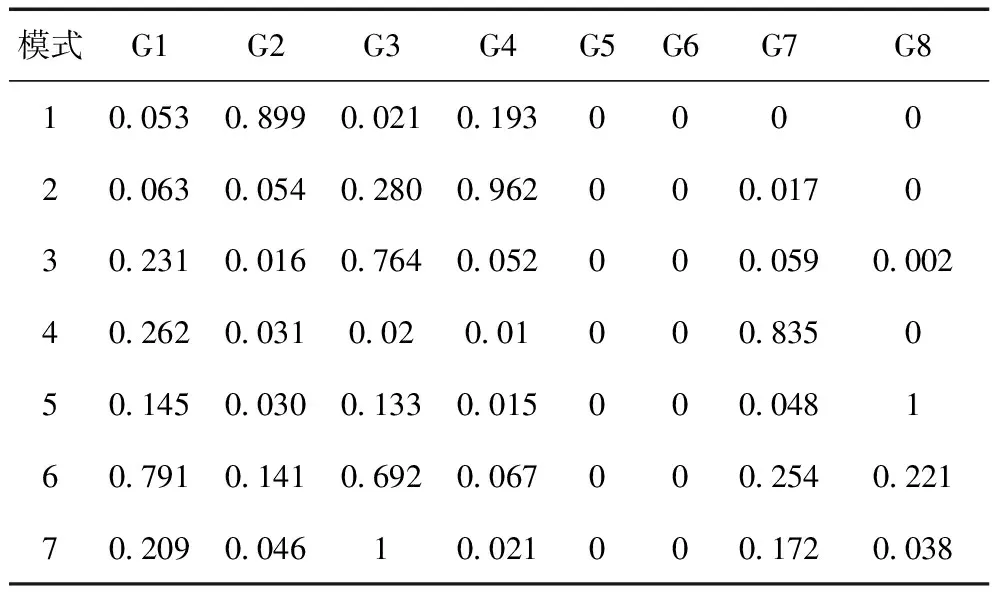
表2 各机组对各模式的参与因子

基于以上分析，在转动惯量变化和不变两种情况下，分别研究光伏并网对各个模式阻尼特性的影响。

3.1 转动惯量变化

大规模光伏并网后，为平衡系统功率，需要将部分发电机退出运行。作为静止发电单元，光伏替代发电机必然会造成系统转动惯量的减少，下面研究光伏等容量替换发电机对各个机电振荡模式的影响。

接入等容量光伏后各模式的阻尼比与被替换机组在光伏接入前振荡模式中参与因子的关系如图5所示。

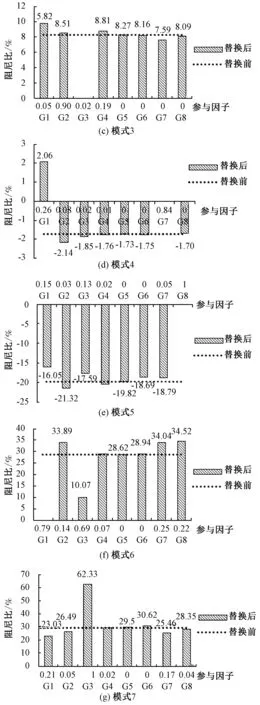
图5 光伏等容量替换发电机组前后阻尼变化

由图5(a)可知，当替换G2时，模式1消失；替换G4时，模式1的阻尼比显著降低；替换G2、G3时，阻尼比略微增加；而替换其它机组时，阻尼比几乎保持不变。各机组对于模式1的参与因子大小关系为：G2>G4>G1>G3>G5=G6=G7=G8=0，由此分析可以得到光伏并网对于低频振荡模式的影响与各被替代机组的参与因子相关，G2作为模式1的最相关机组，其退出直接导致了模式1的消失，被替换机组对模式1的参与度越高，对其阻尼比的影响则越大；反之，则影响越小。同理，G1、G3、G4、G7、G8分别为模式6、模式3、模式2、模式4、模式5的最相关机组，当等容量光伏并网替换G1时，模式6消失；替换G3时，模式3消失；替换G4时，模式2消失；替换G7时，模式4消失；替代G8时，模式5消失。而G5、G6对各个振荡模式的参与因子几乎都为0，因此等容量光伏并网替换G5、G6时，各个机电振荡模式的阻尼比几乎没有变化。根据以上分析，可以得到以下结论：

1)当光伏并网替代同步发电机时，会相应的减少一个机电振荡模式。

2)光伏并网后对系统机电振荡的影响有可能是正面的，也有可能是负面的。

3)接入等容量光伏对机电振荡模式的影响程度与被替换机组在光伏接入前振荡模式中参与因子有关，若被替换机组为机电振荡模式的最相关机组，则该模式消失，同时，参与因子越大，对机电模式的影响则越大，若参与因子为0，则没有影响。

3.2 转动惯量不变

一般来说，同步发电机组的单机额定功率在300～1 000 MW之间，大于大多数的大型光伏电站的容量，因此需要研究光伏替代部分发电机有功出力的情况，即光伏接入后发电机组相应减少对应的容量。

分别以母线24、母线18、母线31为光伏接入点，并根据光伏并网容量减少相应的发电机有功出力，各模式的阻尼比变化与光伏并网容量之间的关系如图6所示。

图6 不同并网容量下各模式阻尼比变化曲线

如图6(a)所示，当光伏并网点为母线24时，G1减少相应的有功出力，随着光伏并网容量的增加，模式1和模式2的阻尼比几乎没有变化，而模式3、模式4以及模式6的阻尼比则首先随着并网容量的增加而减小，但随着容量的进一步增加，其阻尼比则增加，而模式5和模式7的阻尼比则随着光伏接入容量的增加而增加，当并网容量达到500 MW时，其阻尼比则降低。如图6(b)所示，当光伏并网点为母线18时，随着光伏并网容量的增加，各机电振荡模式的阻尼比基本保持不变。如图6(c)所示，当光伏并网点为母线31时，模式5的阻尼比随着光伏并网容量的增加而上升，而模式6的阻尼比则先随着并网容量的增加而增长，接着其阻尼比略微下降，几乎保持不变，而其余模式的阻尼比则一直保持不变，不受光伏并网的影响。结合表2中G1、G5、G8对各个模式的参与因子，分析可得：

1)光伏并网不会产生新的机电振荡模式；

2)光伏并网点以及并网容量等因素对系统机电振荡模式的影响与并网点处发电机对该模式的参与因子有关，若并网点处发电机参与了相应的低频振荡模式，光伏并网对该模式会产生一定的影响，且影响程度与参与因子的大小成正相关，而影响是正面的还是负面的则不确定。

4 结论

主要研究了大规模光伏接入对区域互联系统的机电振荡特性的影响，以8机36节点系统为例，得到以下结论：

1)光伏作为零惯量单元，其并网不会直接影响系统的低频振荡。转动惯量不变时，光伏并网不会产生新的低频振荡模式，而转动惯量变化时，随着同步发电机的退出，系统会相应地减少一个振荡模式；

2)光伏并网对系统阻尼特性的影响可能是正面的，也可能是负面的。因此针对可能出现的负面的影响，需要进一步对附加阻尼控制器进行研究。

3)光伏并网点和并网容量等因素对各振荡模式的影响与并网点处发电机对各模式的参与因子有关，参与因子越大，影响越大，反之则影响很小。