高维球及其在物理学中的应用

2018-12-06赵秋月吴文良

昭通学院学报 2018年5期

赵秋月，吴文良

（昭通学院物理与电子信息工程学院，云南昭通 657000）

0 引言

高维球(又称超球)作为二维平面上的圆和三维现实空间的球在更高维空间延拓的数学概念，可以使一些复杂的物理问题简单化，被广泛应用于各个领域。然而由于高维球概念的抽象性，对于物理学的学生来说理解和应用存在一定困难。现有的文献如[1-3]等虽然对高维球概念进行了研究和讨论，但对初学者来说仍然较为难以理解和掌握。对高维球概念及其相关计算公式作一科普性的简明的分析和介绍，对物理专业的学生以及邻近专业的学生来说不无益处,本文对此作一尝试。

1 从二维平面的圆到三维空间的球

1.1 二维平面的圆

圆是一种美妙的图形。中国古代墨家的经典著作《墨经》中就有“圆，一中同长也”的记载，汉代的算书《周髀算经注》中也有“圆径一而周三”的认识。古希腊的学者亚里士多德认为，地上的物体的自然运动是卑贱的直线运动：火和气往上运动，土和水往下运动；而天上的星体的自然运动则是高贵的圆周运动。古希腊天文学家进一步认为肉眼可见的五颗行星分别在绕动点作圆周运动，这些圆周称为本轮。而作为动点的每个本轮的圆心又在绕地球作圆周运动。这些圆周被称为均轮。此后为了使理论和新的观测事实相符合，学者们通过用在本轮之上再加本轮的方法，使得亚里士多德和托勒密的地心说成为了一门非常繁复的体系。即便在这一理论被哥白尼的日心说证伪之后，哥白尼仍然认为行星绕太阳的运动是完美的圆周运动，他在《天体运行论》中说：“在所有行星的中心居住着太阳，在这个位置它可以一瞬间照亮整个宇宙。对于这个最壮丽的神殿，谁能将这盏明灯安放到另外或更好的地方？”开普勒把这盏明灯安放到了更好的地方，他发现太阳并不在行星圆轨道的中心，而是在行星椭圆轨道的一个焦点上。

用数学专业的语言来说，圆是由点构成的称为平面的集合的子集。这个子集可以是圆周，即平面上到给定点距离相等的点的集合；可以是圆周内部的点组成的开集，称为开圆；也可以是圆周连同内部的点组成的闭集，称为闭圆。在笛卡尔平面直角坐标系中，这三个集合可以分别用坐标(x,y)表示为{(x,y)|(x-x0)2+(y-y0)2=R2},{(x,y)|(xx0)2+(y-y0)2＜ R2}和 {(x,y)|(x-x0)2+(y-y0)2≤ R2}。其中点(x0, y0)称为圆的圆心，R称为圆的半径。在圆周所在平面上经过圆心的直线与圆周交于两个点，这两个点构成的线段称为圆的直径，其长度为2R，圆周的长度与直径之比称为圆周率，用π表示。因此半径为R的圆周长度为2πR。

要计算圆的面积需要用到积分。把半径为R的圆分割成一个个宽度都是dr的无穷多个圆环，其中内外半径分别是r和r+dr的圆环的面积等于长和宽分别为2πr和dr的矩形面积。因此半径为R的圆的面积等于这无穷多个圆环的面积之和，即：

可以用另外一种积分方法计算圆的面积：平行于圆的某条直径把圆分割成无穷多条，每一条近似看作矩形，它的宽度为dy, 长度l随着到圆心的距离|y|而变化：.因此半径为R的圆的面积等于这无穷多个近似矩形的面积之和，即：

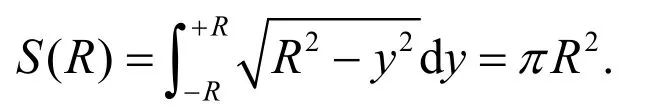
从运动学的角度，可以把半径为R的圆周看作是一条长为R的线段绕经过线段的一个端点且垂直于线段所在直线的某条轴旋转时线段另一端点的轨迹。而作为闭集的圆则是整条线段旋转一周所成的图形。如果把半径为R的圆周投影在一条直线上，得到的是距离为2R的两个点；而作为闭集的圆的投影则是由那两个点构成的长度为2R的线段。

1.2 三维空间的球

将半径为R的圆周绕它的某条直径旋转一周，就得到三维空间中的一个球表面，即通常意义下的球表面。球表面内部的点构成的集合，称为开球，开球与其表面的并集，称为闭球。球表面、开球和闭球都可以简称为球，显然它们都是三维空间的子集。在笛卡尔（三维）空间直角坐标系中，这三个子集用坐标(x, y, z)分别表示为{(x,y,z)|(xx0)2+(y-y0)2+(z-z0)2=R2}, {(x,y,z)|(x-x0)2+(y-y0)2+(z-z0)2＜ R2}和{(x,y,z)|(x-x0)2+(y-y0)2+(z-z0)2≤ R2}。其中点(x0, y0, z0)称为球的球心，R称为球的半径。

我们可以把圆看作是三维空间中的球在二维平面上的投影。从而可以用如下的方法来计算球的体积。把球沿平行于过球心的某个球面将球体分割成无穷多个近似圆柱，每个圆柱的高为dz, 底面积为圆的面积。底面圆的半径随距球心的距离|z|而变化，并且圆的半径与圆距球心距离的平方和就是球半径R的平方，因此圆的体积为：

也可以把球分割成无穷多个厚度为dr的同心球壳，设半径为r的球的表面积为S（3r）, 则有

把R看作变量，将等式两边对R求导数，得

再由已知的球的体积，得到半径为R的球的表面积公式：

2 往更高维拓展

2.1 四维超球

在现实的三维空间中，我们不能像旋转圆得到球一样通过旋转把球变为其他的几何体，但是我们仍可以把三维空间中的球想象为四维空间中的超球在三维空间中的投影。与三维空间中的球相类似，四维空间中的超球是四维空间的子集。所谓四维空间，是指由所有有序实数组（x1, x2, x3,x4)构成的集合，每一个实数组称为四维空间中的点。四维超球可以指称超球的表面可以指称超球的内部或者二者的并集其中R为四维超球的半径，点为四维超球的球心。可以把四维超球分割成无穷多个“球柱”，每个球柱的高为dx4，“底面积”分别是三维空间中半径为的球的体积，从而得到四维超球体的体积公式：

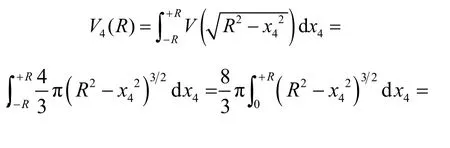
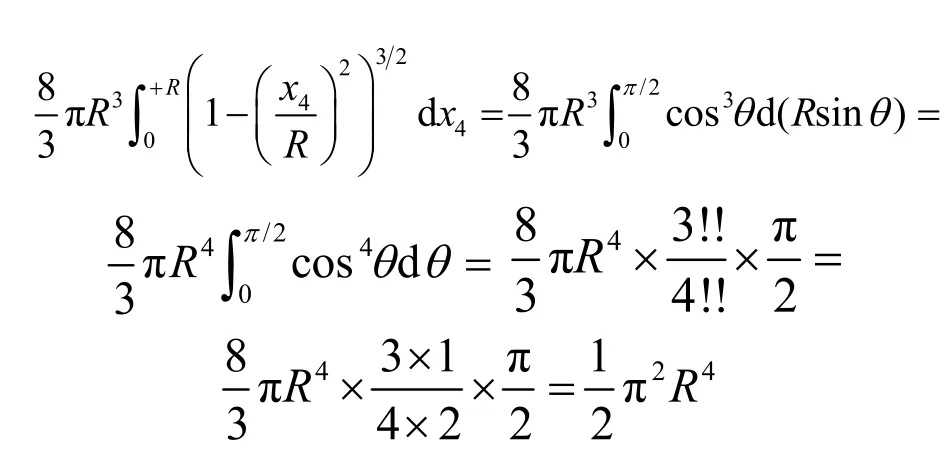
式中符号“n!!”称为n的双阶乘，表示所有不大于n且与n同奇同偶的正整数的乘积。也可以把四维超球分割成无穷多个同心超球壳，从而得到四维超球的表面积公式：

2.2 n维空间中超球的体积和表面积

一般地，n维空间中超球是n维空间的子集，是指由所有有序实数组（x1, x2, …,xn)构成的集合，每一个实数组称为n维空间中的一个点。n维超球可以指超球的表面可以指超球的内部或者是二者的并集其中R为超球的半径，点为超球的球心。可以把n维超球分割成无穷多个超球柱，每个超球柱的高为dxn，“底面积”分别是n-1维空间中半径为的球的体积，从而得到n维超球体的体积递推公式：

也可以把n维超球分割成无穷多个同心超球壳，从而得到n维超球的表面积公式:

2.3 二维球和一维球

高维球是低维球在更高维空间中的延拓，低维球则是高维球在较低维空间中的投影。因此，我们可以把圆称为二维球，它的“球心”即为圆心，“体积”就是圆的面积，而“表面积”则是圆的周长。圆在一维平直空间中的投影是一段线段，因此可以把线段称为一维球，它的“球心”即为线段的中点，它的“体积”即为线段的长度，而它的“表面积”则为2，即线段两个端点的“大小”。

3 量纲分析导出n维超球的体积和表面积

3.1 n维超球的体积和表面积的一般公式

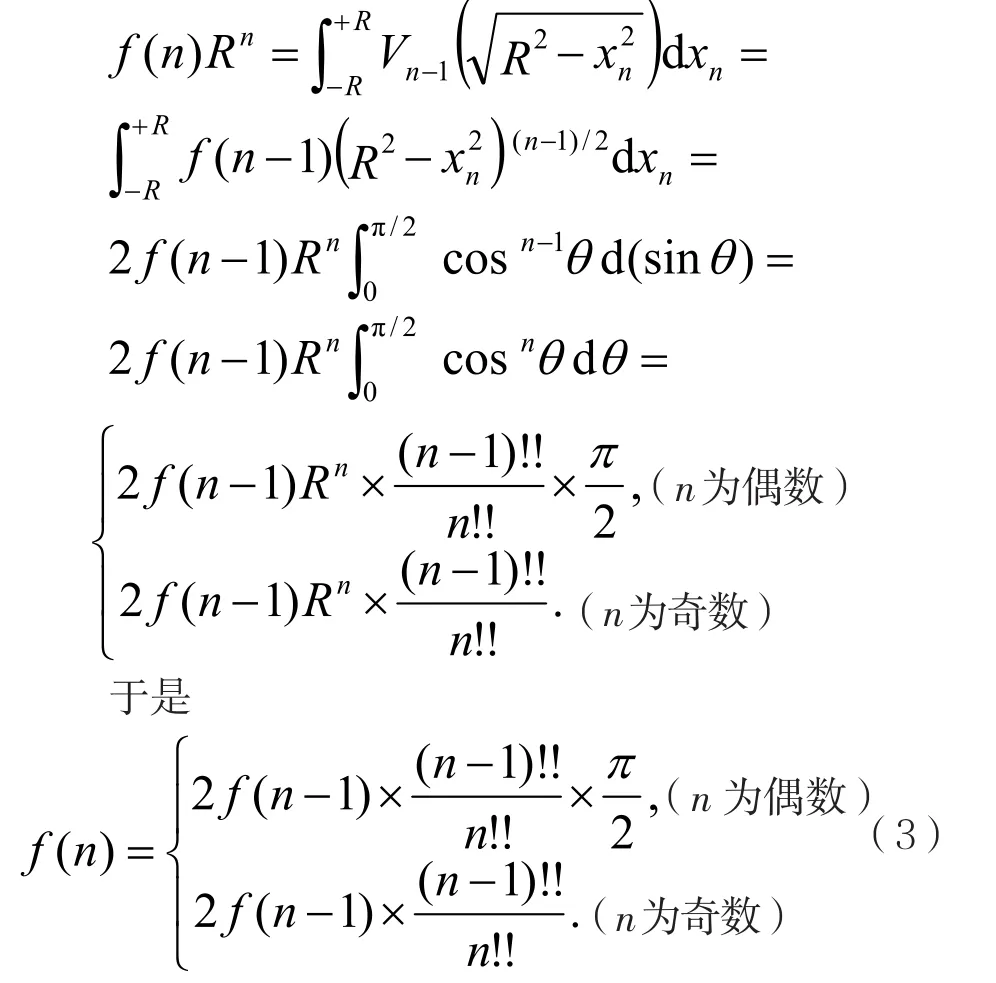
由于 f(2)=π, 故

代入（2）式，得

借助伽玛函数

于是（4）和（5）可改写为：

（4）～（7）即为高维球的体积公式和表面积公式。

3.2 五维、六维和七维球的体积和表面积

由n维超球的体积和表面积的一般公式，可以求出五维、六维和七维球的体积和表面积：

3.3 零维球

“一维球”线段在零维空间中的投影是一个点，因此可以把点称为“零维球”。它的“球心”与“球”融为一体，“体积”等于1，与“半径”无关：“表面积”等于0.将f(0)=1和f(1)=2代入（3）式，得到0!!=1.此即0的双阶乘的定义。

4 高维球在物理学中的一些应用

4.1 理想气体熵的计算

物理学中熵的概念有热力学熵和统计物理学熵之别。热力学熵是统计物理学熵在热力学中的表现，统计物理学熵是热力学熵在统计物理学中的本质。热力学熵又称克劳修斯熵，定义为可逆过程的热温比，它是一个状态量，当系统从平衡态A经可逆过程变为平衡态B时，系统的熵变为：

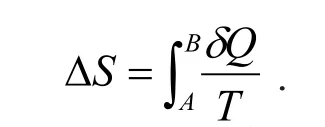
在热力学中，可以任意选择一个平衡态的熵等于零。而在统计物理学中的熵又称玻尔兹曼熵，被定义为系统处于某一平衡态的热力学概率W的对数，即

式中kB为玻尔兹曼常数，它在式子中的出现是由于在热力学中把熵定义为热温比，而温度则由各种不同的温标所定义。一旦把它规定为1（在自然单位制中），我们就可以定义一种新的温标。

对于理想气体来说，可以把体积为V，物质的量为n、单个分子质量为m的单原子分子理想气体系统看作质点数为N=nNA的质点系，系统的热力学能等于质点系的动能，即所有质点动能之和，它决定了系统的热力学温度T。系统处于热力学温度T的平衡态的热力学概率W正比于微观状态数Ω，即系统总动能为E=3kBT/2的相点数。在经典力学中，系统的能量可以取连续的值，因而相点数是无限的。可以认为微观状态数与相应的相空间体积成正比。对于单原子分子理想气体来说，系统的能量与分子的坐标无关，只要系统分子的速度分布在3N维速度空间中的半径为v的球面上，则系统的热力学能即为E=mv2/2.因此，系统能量介于（E1，E1+ΔE）之间的相空间体积为

而系统能量介于（E2，E2+ΔE）之间的相空间体积为

于是系统能量为E1与E2的微观状态数之比为

因而一定物质的量的理想气体，在等容变化过程中热力学能由E1变化到E2，发生的熵变为：

式中R为气体普适常量。能够取近似是因为N对宏观系统而言是一个很大的数。根据焦耳定律，理想气体的热力学能只是温度的函数，因而

这正是热力学中所得到的结果。

4.2 n维球坐标系及其一些应用

平面解析几何中的极坐标系可以看作二维球坐标系，它用极径ρ和一个极角θ来确定平面上一点的位置；空间解析几何中是三维球坐标系，它用矢径r和两个角坐标θ,φ来确定三维欧几里德空间中一点的位置。一般地，n维球坐标系用矢径r和n-1个角坐标θ1,θ2, …，θn-1来确定n维欧几里德空间中一点的位置。设半径为r球心在原点的n维球面上的一点P在n维笛卡尔直角坐标系中的坐标为（x1,x2, …,xn)，则θ1定义为径矢与第n条坐标轴的夹角，即有xn=rcosθ1。当θ1=0时，P点在垂直于第n条坐标轴的n-1维欧几里德空间中的投影是原点，P点的其余直角坐标x1，x2，…，xn-1均为0；当θ1≠0时，P点在垂直于第n条坐标轴的n-1维空间中的投影P1位于球心在原点半径为rsinθ1的n-1维球面上。从而可将θ2定义为与第n-1条坐标轴的夹角，即有xn-1=rsinθ1cosθ2。类似地可以定义其余角坐标。需要注意的是：θn-1并不是与第2条坐标轴的夹角（其中Pn-2为Pn-3在二维平面上的投影），而是与第1条坐标轴的夹角，其取值范围为0≤θn-1＜2π。其余角坐标的取值范围均为0≤θi＜π(1≤i≤n-2).由P点的n维球坐标（r，θ1，θ2，…，θn-1）,可求出其直角坐标（x1，x2，…，xn)：

应用高维球坐标系，李春树[2]对带电胶体系统中排空作用开展了研究，翁爱华等[3]对大地电磁测深资料作了分析；刘云等[4]讨论了静态荷电球体的Einstein-Maxwell场方程；王沂轩等[5]计算了三电子原子的基态能态；冯名诚等[6]研究了弱磁场中的二维D～-中心。囿于笔者学识所限，这里不再一一详加讨论。