一种考虑震源与传播路径的重力坝地震 响应分析的新方法

贺春晖， 陈 林

(中国电建集团成都勘测设计研究院有限公司，四川 成都 610072)

0 前 言

影响大坝动力响应分析准确性的因素主要包含三个方面的内容：地震波输入、坝-地基-库水系统、坝体材料的强度评价准则。坝-地基-库水系统在理论和数值模型方面都已经相对成熟[1-3]，而集中于材料动力特性以及强度评价标准的研究也取得了一定的成果[4]，但是同样对于大坝动力反应影响很大的地震波输入问题却并没有得到很好的解决。依据水工建筑物抗震规范，目前水工建筑抗震设计中确定基岩加速度峰值的方法一般采用《中国地震烈度区划图》确定基本烈度，对于大型工程设防依据专门的地震危险性分析提供的基岩峰值加速度成果评定。上述两种方法都是基于已有的地震实测记录，利用概率和统计的宏观分析方法得出需要的设计地震动参数。现行的水工建筑抗震设计中，获取地震动时程的方法有如下几点不足：

(1)工程场址所在的局部小范围区域内，大多缺乏足够的、可以用作统计样本的实测记录，导致基于这些样本进行的外推本身准确性不高；

(2)外推时依据统计规律得到的衰减关系，不能反映场地特殊地形地质条件的影响；

(3)确定峰值加速度后，根据规范给出的设计反应谱求得时间历程，无法反映由不同地震特异性的影响。

另外，不同的输入机制对结果也会造成影响。对于高拱坝或重力坝这样的空间大跨度结构，采用均匀输入显然是不合适的。对于极少数有实测地震记录的坝址[2]，可以考虑非均匀输入，但是对于其他大多数情况，没有足够的依据来考虑由于局部场地条件导致的幅差和相差。目前已有部分学者开始将震源和水工结构作为一个整体进行分析：张翠然等[5]通过随机方法模拟了大岗山水电站场址的最大可信地震；Bayraktar[6]通过选取对应于不同震源机制的实测地震记录研究了断层破裂与大坝动力响应之间的关系。Keaton[7]通过选取合适的震源参数得到加速度时间历程，以此为基础计算胡佛大坝公路桥的地震非线性响应。Zarafani[8]采用高低频结合的方法计算近断层大坝的反应谱。

本文综合考虑地震震源、传播路径以及场地反应得到适合于大坝地震分析计算的空间非均匀地震动，即：作为大坝动力分析的输入地震波能够包含特定震源机制，传播路径和场地地形、地质条件等信息，以实现合理的非均匀输入，使大坝地震反应分析的输入环节更具可靠性和说服力。本文提出的方法通过局部场地在地震学和工程学之间建立联系，大坝结构动力分析基于现有的、较为成熟的模型进行，而局部场地地震波场模拟的上游工作则基于地震学方法展开。在地震学中，目前模拟工程适用的宽频带(0～10 Hz)地震波采用较多的是混合方法(Hybrid Method)[9-11]，即分别用随机方法(Stochastic Method)[12]模拟高频部分，确定性方法(Deterministic Method)模拟低频部分，选取适当的交叉频率，滤波后在频域或者时域内叠加得到宽频带地震波波形。随机方法利用Boore的ω-2加速度幅值谱经过傅里叶逆变换得到。确定性方法多采用有限差分法或有限元法等数值方法。有限差分法适应复杂地形的能力弱，需要较多节点才能达到一定的精度，且有限元法则可能出现频散或者伪波[13]。谱元法是一种高阶有限元法，最早是Patera于1984年计算流体力学的时候提出，该方法融合了传统有限元方法的灵活性和伪谱法的精度[14-15]。1998年Dimitri Komatitsch首次采用基于Legendre多项式和GLL积分的谱元法求解弹性波动方程，表明该方法具有收敛快、精度高等优势。本文利用谱元法进行探讨性分析，选取模型范围较小，通过假定震源频率和细化网格，可以使波的频率范围包含重力坝结构的主要振型。

1 震源与传播路径模拟

1.1 震源模拟

本文基于二维模型讨论重力坝的动力响应与行波效应及震源相对位置的关系，暂且不讨论断层空间效应的影响，故将震源简化为点源，震源时间函数采用Ricker子波，时域表达式见式(1)，频域表达式见式(2)，峰值频率为4 Hz的Ricker子波的时域波形和幅值谱，如图1所示。

(1)

(2)

1.2 谱元法模拟传播路径

谱元法的基本出发点和有限元一样，也是由伽辽金加权余量法建立有限元的表达格式，不同之处在于它在每个单元上使用谱方法，即：将形函数取为无限可微函数(如Fourier级数)，从而可以变换到谱空间求解。数值方法中，一般选取截断的正交多项式(Chebyshev或Legendre多项式)。Dimitri Komatitsch首先基于Legendre多项式对弹性波方程求解。Legendre多项式递推式如式(3)：

(3)

式中L0(x)=1，L1(x)=x。

谱元法和一般高阶有限元方法差别就在于单元内插值点和数值积分点的选取，Legendre谱元法将Legendre多项式的极值点作为单元内插值点。以一维单元情形为例，取4阶Legendre多项式，共有5个GLL点，其广义坐标向量为(-1.000 0，-0.654 7，0.000 0，0.654 7，1.000 0)，相应的5个拉格朗日插值多项式图像如图2所示。数值积分采用Gauss-Lobatto积分，积分点位置和插值点位置重合，各点积分权值为：

(4)

式中j=1,2,…,5。

对于5个GLL点的一维单元，则计算出各个点的权值分别为(0.100 0，0.544 4，0.711 1，0.544 4，0.100 0)，对于Lagrange插值多项式有Li(xj)=δij，质量矩阵写为：

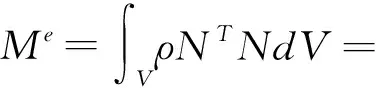
(5)

矩阵中的元素数值积分后，由公式(6)：

(6)

得到严格对角化的质量矩阵：

(7)

对于二维情形，可由一维插值函数的张量积表达，位移的展开形式如式(8)：

图1 Ricker波的时域波形和幅值谱

(8)

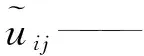
φi(ξ)——一维插值形函数。

三维情形与二维类似。

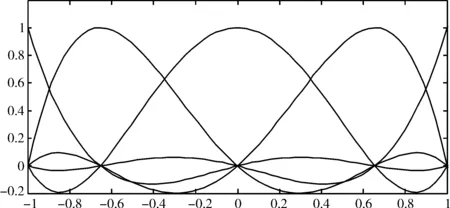
图2 4阶谱单元的拉格朗日插值函数

2 重力坝地震分析模型

2.1 实现方法

传统的重力坝动力计算中，采用的是沿截断地基均匀输入的方法，即从远处传来的地震波传到近场边界时，各个点的运动形态一致，对于大坝等大跨度结构，截取的人工边界的范围也相应较大，这种假设显然是不合理的。采用图3所示的方法将自由场加速度时程转换成等效节点反力时程输入建基面，并在地基截断处考虑黏弹性人工边界，即可模拟此非均匀性。而自由场加速度则是通过模拟震源和传播路径获得，相比传统方法更具有说服力。

如图3所示，分三个步骤进行：

(1)用谱单元离散传播路径，通过选取适当的网格尺寸和时间步长，确定有效的频率范围。设定震源，激发弹性波并利用谱元法求解波动方程，得到自由场建基面各点的加速度响应。

(2)将近场地基作为子结构，在边界上施加黏弹性边界条件以模拟辐射阻尼效应，将第(1)步求得的加速度时程输入建基面各点求得相应的节点反力时程。

(3)最后加上重力坝结构，并在建基面各点输入等效节点反力时程，用有限元方法对重力坝进行动力响应分析。

2.2 SPECFEM2D程序网格敏感分析

二维谱单元网格型如图4所示，长度为10 km，深度为3 km。震源在距离左侧边界2 km处，接收点距离右侧边界4 km，震源到接收点距离为4 km。单元采用4阶Legendre多项式插值，每个单元含有5×5=25个GLL点，分别计算粗细网格的有效频率范围。粗网格谱单元尺寸为100 m×100 m，包含3 000个单元，总自由度数为97 042；细网格谱单元尺寸为50 m×50 m，包含12 000个单元，总自由度数为386 082。

粗细网格分别计算得到的不同激震频率下接收点x向位移时程如图5和图6所示，分别用粗细网格计算不同频率的波，ricker波主频分别为2 Hz、4 Hz、6 Hz、8 Hz、10 Hz。可以看出，由于数值离散，粗网格模型在主频为4 Hz的时候波形和频率成分都发生了改变，而细网格模型在主频为4 Hz的时候仍然能够保持原有的波形和频率成分。

2.3 重力坝数值算例

2.3.1 计算条件及参数

取典型重力坝剖面，体型参数为高200 m，底宽140 m， 顶宽20 m， 坡比1 ∶0.7。 地基分别向上游、下游和竖直向下的方向延伸1.5倍坝高(300 m)，如图7所示。坝体混凝土材料密度为2 400 kg/m3，弹性模量2.2E+10Pa，泊松比0.167，地基材料密度2 650 kg/m3，弹性模量2.5E+10Pa。坝体网格尺寸约10 m。坝体单元采用4节点平面应力单元，地基单元采用4节点平面应变单元。

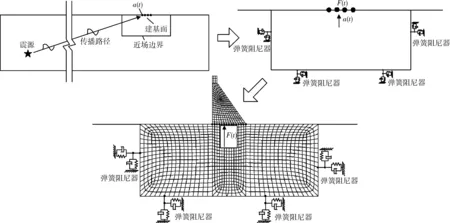
图3 计算过程示意

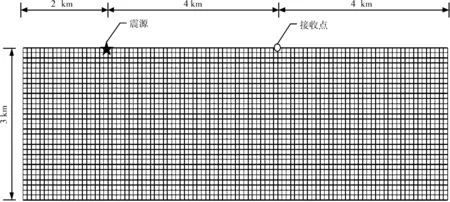
图4 网格模型示意

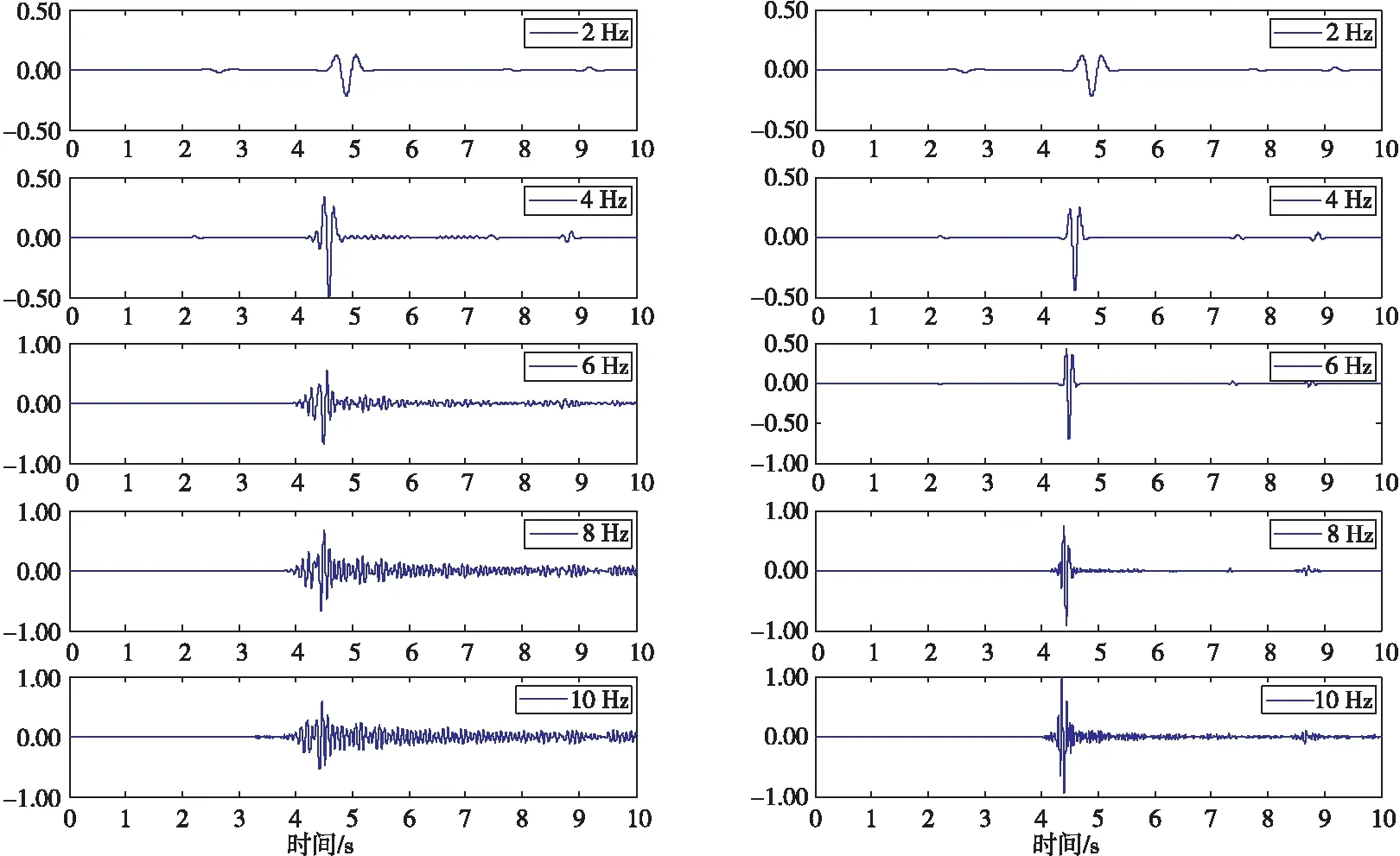
图5 粗(左)细(右)网格下不同激震频率下波的传播对比

图6 粗(左)细(右)网格下不同激震频率下观测点位移幅值谱

谱通过自振分析得到重力坝前10自振阶频率以及各阶模态的振型参与系数见表1。

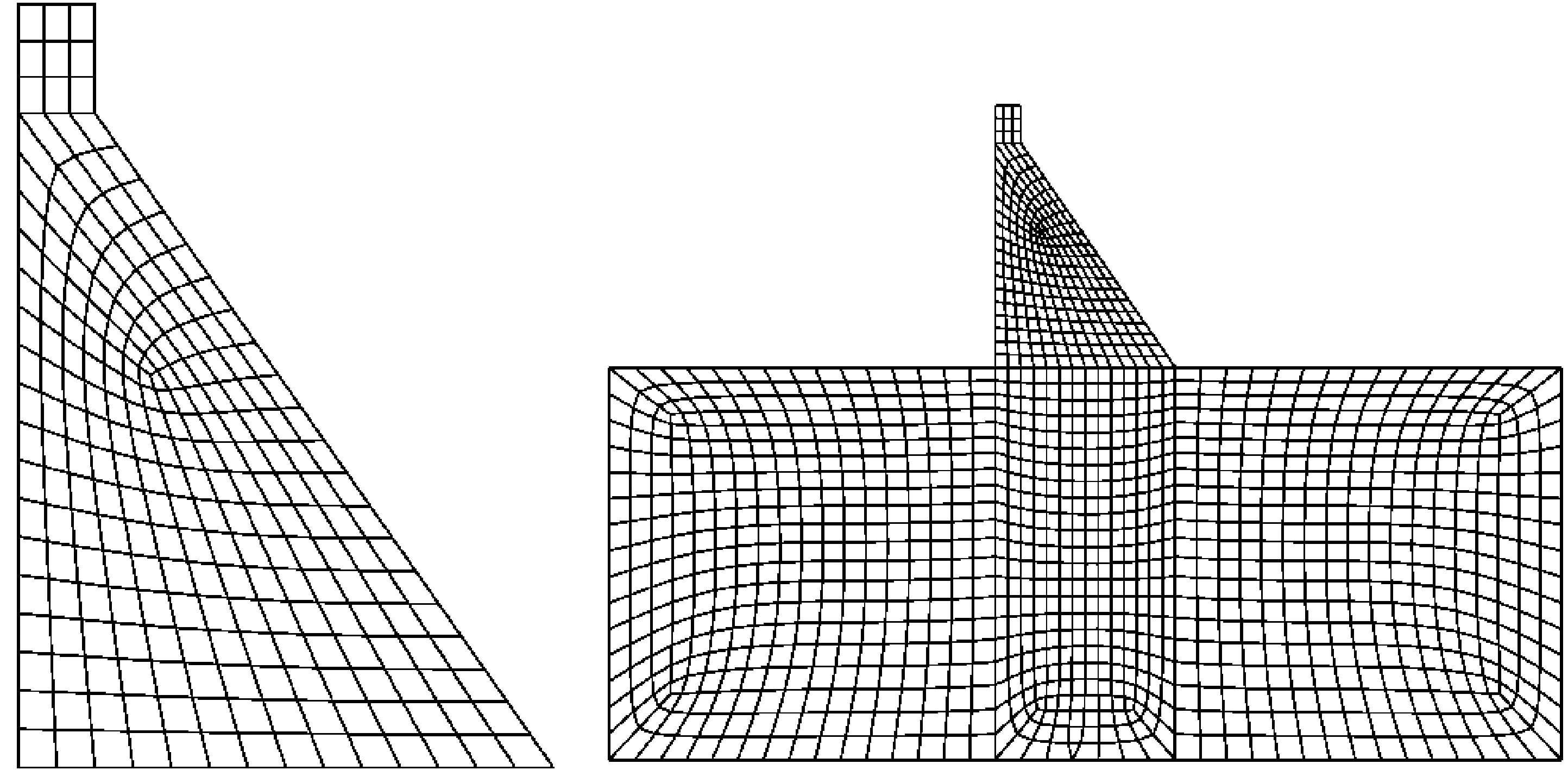
图7 坝体及地基有限元网格

模态12345678910频率/Hz1.4103.1883.3725.6318.7168.86912.50113.34814.23916.212参与系数(x-分量)参与系数(y-分量)2.1660.498-2.0610.7680.086-1.7291.2110.5450.313-0.476-0.400-0.3550.2060.0380.0590.051-0.054-0.091-0.060-0.064

根据第3.2节所述，选取细网格模型模拟波的传播过程，设震源位移时间函数为主频4 Hz的Ricker子波，计算的加速度(归一化)结果作为地震荷载输入重力坝。波形和傅里叶谱如图8所示。

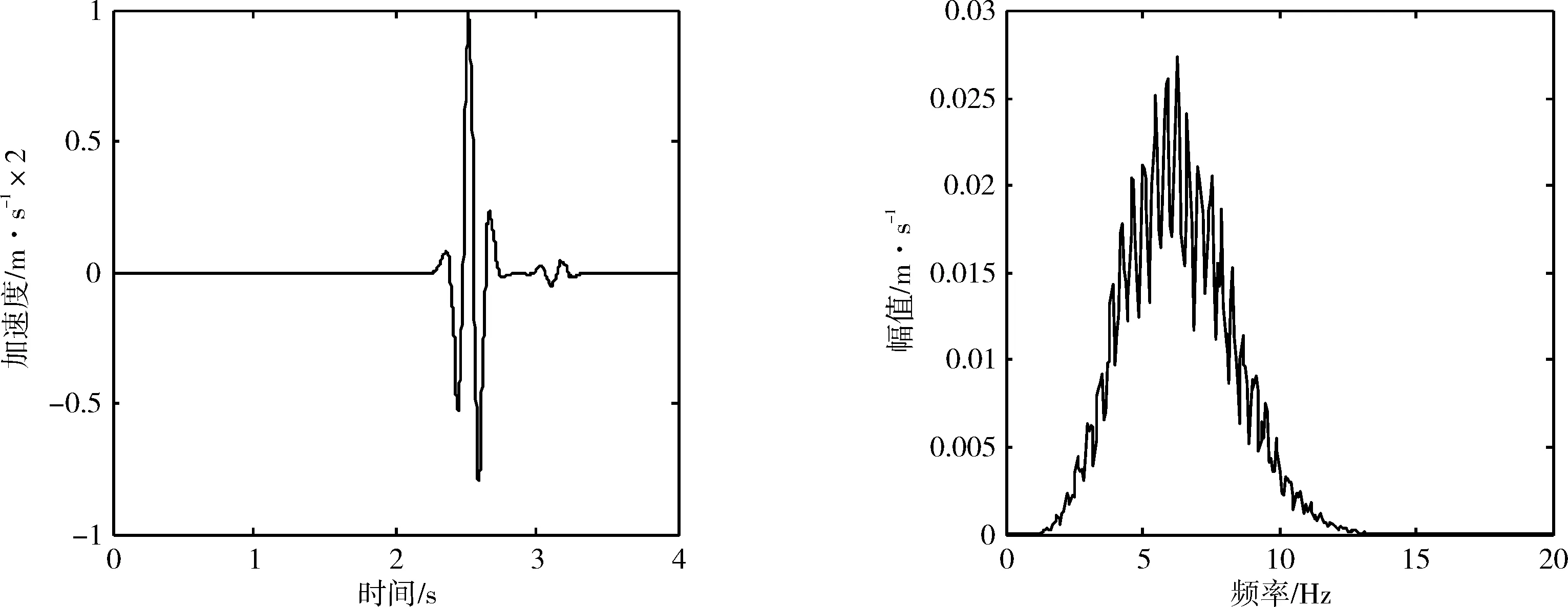
图8 输入加速度波形和傅里叶谱

2.3.2 传播介质的影响

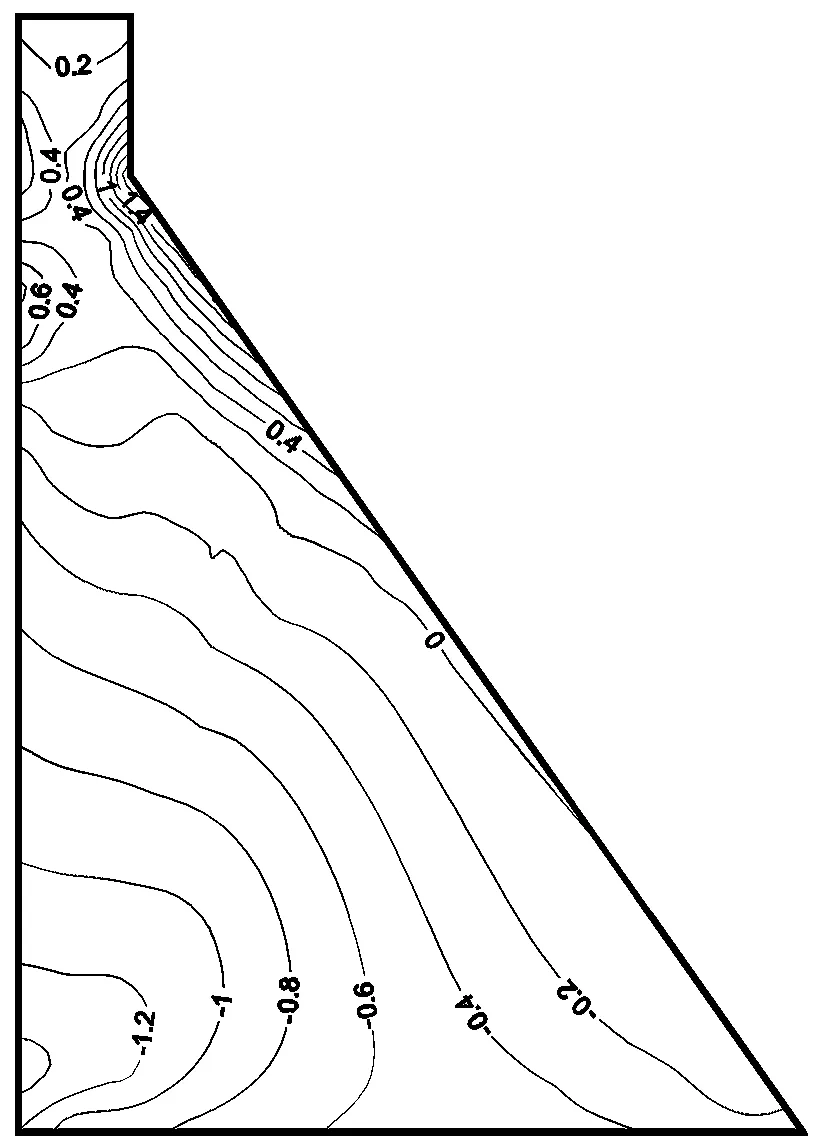
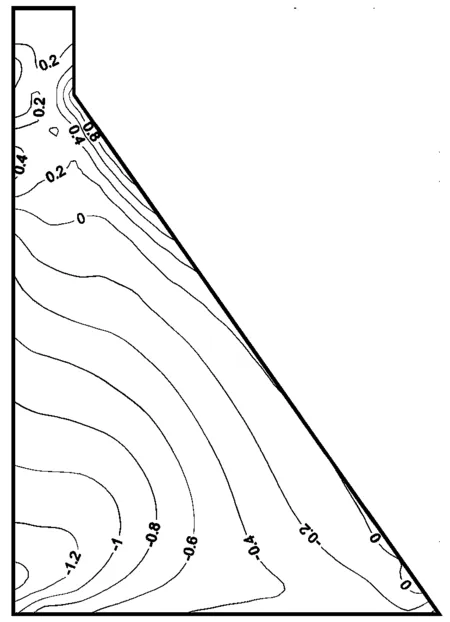
本节考虑传统的均匀输入方式和考虑地震波传播过程的非均匀输入对重力坝动力响应结果的影响。如图9(a)所示，输入地震波的有限元节点分别编号为①～。图9(b)给出了均匀输入时各个节点的加速度时程，可以看到各点运动是一致的。图9(c)给出了非均匀输入时各节点的加速度时程，各个节点之间存在幅差和相差。非均匀输入时分别考虑S波传播速度Vs等于2.0 km/s、1.5 km/s、1.0 km/s三种情形。计算结果如图10以及表2所示。考虑幅差相差的非均匀输入得到的最大主应力结果明显区别于均匀输入：

(1)坝体上部，非均匀输入的应力结果小于均匀输入，均匀输入条件下，坝颈部上游面和下游面分别出现0.6 MPa和1.4 MPa的拉应力。而非均匀输入且波速等于2.0 km/s时，相应部位的拉应力分别降至0.4 MPa和1.0 MPa。当波速进一步减小，即非均匀性增强时，坝体动力响应减弱变得更加明显。

(2)坝底处，非均匀输入导致最大主应力值有所增大，幅差相差在坝体引起的各点运动的不一致有增大坝底处动力响应产生的拉应力的趋势。

另外，图11给出了坝顶的动力响应过程，可以看到非均匀输入条件下坝顶点的加速度幅值有所降低。

图9 均匀输入和非均匀输入的加速度时程

(a)均匀输入

(b)非均匀输入，Vs=2.0 km/s

(c)非均匀输入，Vs=1.5 km/s (d)非均匀输入，Vs=1.0 km/s

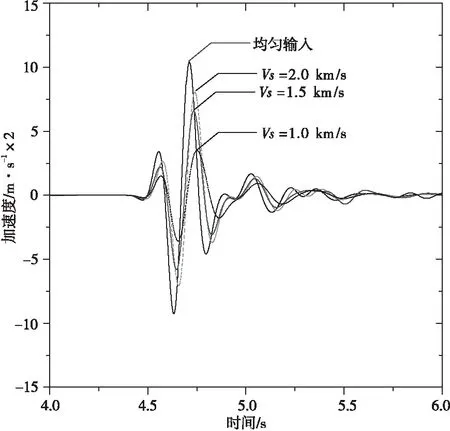
图11 不同输入机制下坝顶的加速度顺河向反应时程

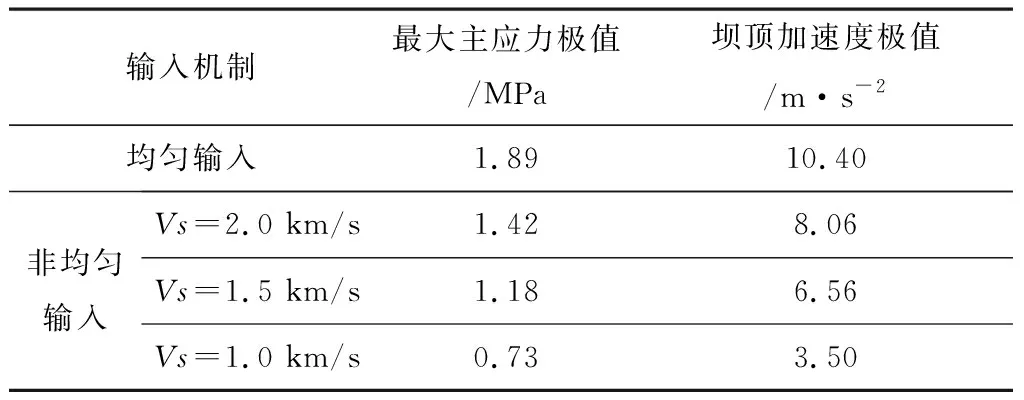
输入机制最大主应力极值/MPa坝顶加速度极值/m·s-2均匀输入1.8910.40非均匀输入Vs=2.0 km/s1.428.06Vs=1.5 km/s1.186.56Vs=1.0 km/s0.733.50

对于一般的工程场址，P波波速约在2～3 km/s，S波波速在1～2 km/s。由上述计算结果可知，实际工程中，地震波的行波效应对坝体动力响应会产生一定的影响。对于重力坝，表现为降低坝顶反应，同时增大坝底附近的拉应力(主要为坝底中部)。对于拱坝结构，其跨度更大，加之峡谷两侧的地形影响，行波效应更加明显，对此需要做专门的三维分析，此处不予详述。

2.3.3 震源位置的影响

前面的内容都是假设震源位于重力坝上游侧，波由上游方向入射。本节讨论波从不同方向传入的影响，设置位于重力坝下游侧的震源，比较不同震源位置对重力坝动力响应的影响。图12表明，考虑静动荷载叠加时震源位置对应力分布结果影响不大，相同的波速下，上游侧震源和下游侧震源的应力分布规律基本一致。但是从图13给出的纯动力反应结果可以看出，震源位置对重力坝的纯动力响应有显著的影响：当震源位于上游侧时，坝踵部位的拉应力较大；而当震源位于下游侧时，坝趾部位的拉应力较大。从整体应力分布来看，整个受拉区有向震源一侧偏移的趋势。不同震源位置条件下，坝体上部应力分布规律仍基本一致。

(a)上游侧震源

(b)下游侧震源

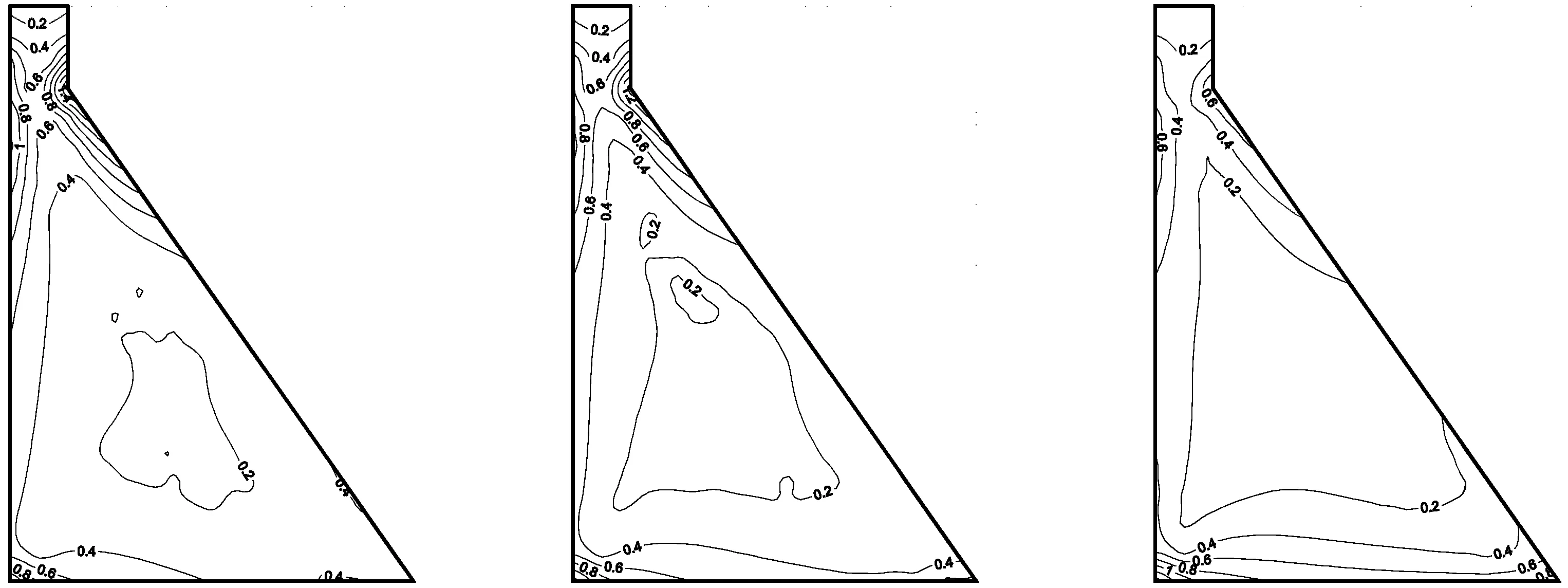
(a)上游侧震源

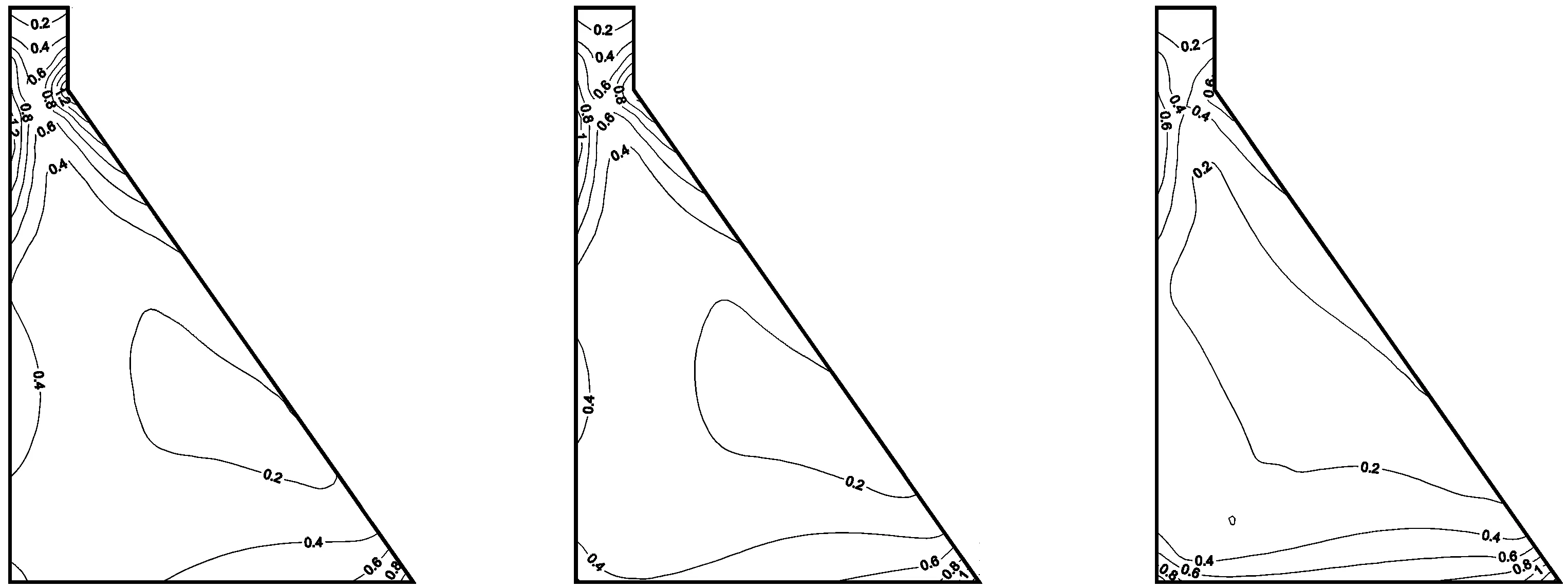
(b)下游侧震源

3 结 论

本文提出的基于地震学方法为大坝动力分析提供输入的方法，比传统输入方法更具有科学性和说服力。通过此方法，可以考虑非均匀输入以及震源和结构相对位置的影响，并且通过重力坝算例分析得到了初步的结论：

(1)考虑非均匀输入的重力坝整体动力响应明显低于均匀输入，但是在坝底部中间小范围区域会出现更高的拉应力，且这种影响随着结构空间尺度的增加而增加，在大型水利工程的设计中应该予以考虑。

(2)震源和结构的相对位置使得重力坝拉应力区趋向于靠着震源一侧偏移，即震源侧的动力响应更高。对这一方面进一步的研究，可以为工程选址和大跨度结构局部加固提供有意义的成果。

本文仅通过较小规模的二维算例，研究了重力坝的动力响应，实现了从震源模拟到结构响应的过程，但是未考虑实际地形和速度结构的影响，根据此思路的进一步的研究工作已经取得成果：基于三维模型利用谱元法进行地震波传播模拟，并且考虑地形地质条件的影响，结合地震学高频随机模拟方法，合成宽频带地震波，以此作为地震动输入用于计算峡谷地形中拱坝的地震响应。