棒状试样拉伸试验不确定度的评定

高江君, 高 虹, 沈卫强, 徐 奇

(江苏武进不锈股份有限公司，江苏 常州 213111)

引 言

对金属材料进行检测或测量时，不管检测方法和仪器设备如何完善，其测量结果都存在着不确定性[1]，不确定度便是由此引入。中国在1999年颁布了相应的标准——JJF 1059-1999《测量不确定度评定与表示》，对不确定度的评定提供了规范。尽管如此，许多从事检测工作的人员依旧对不确定度的评定茫然不解。测量不确定度是表征合理赋予被测量之值的分散性，与测量结果相联系的参数，是测量结果有效性的可疑程度或不肯定程度。

金属材料的拉伸试验属于材料破坏性试验的一种，因其不可再现性，加之众多外界因素的影响，为降低实验室数据检测风险，对金属材料拉伸试验的不确定度评定显得格外重要。本文采用标准样块进行拉伸试验不确定度评定，为广大检测工作者提供对不确定度评定的参考。

1 不确定度评定的基本方法

1.1 建立数学模型

规定塑性延伸强度

Rp0.2=Fp0.2/S0

抗拉强度

Rm=FMAX/S0

断后伸长率

A=(LU-L0)/L0

式中Fp0.2为0.2%非比例延伸下的载荷；LU为断后标距；S0为拉伸试样横截面积；L0为原始标距；FMAX为最大载荷。

1.2 试验方法

本次评定过程使用上海新三思计量仪器制造有限公司生产的CHT-4605型万能试验机，所用试样为钢铁研究总院研制的样品编号为453#10～17的8个标准拉伸试样，证书号为BY20151175，试验在10～35 ℃室温下进行。试验后得到测量结果如表1所示。

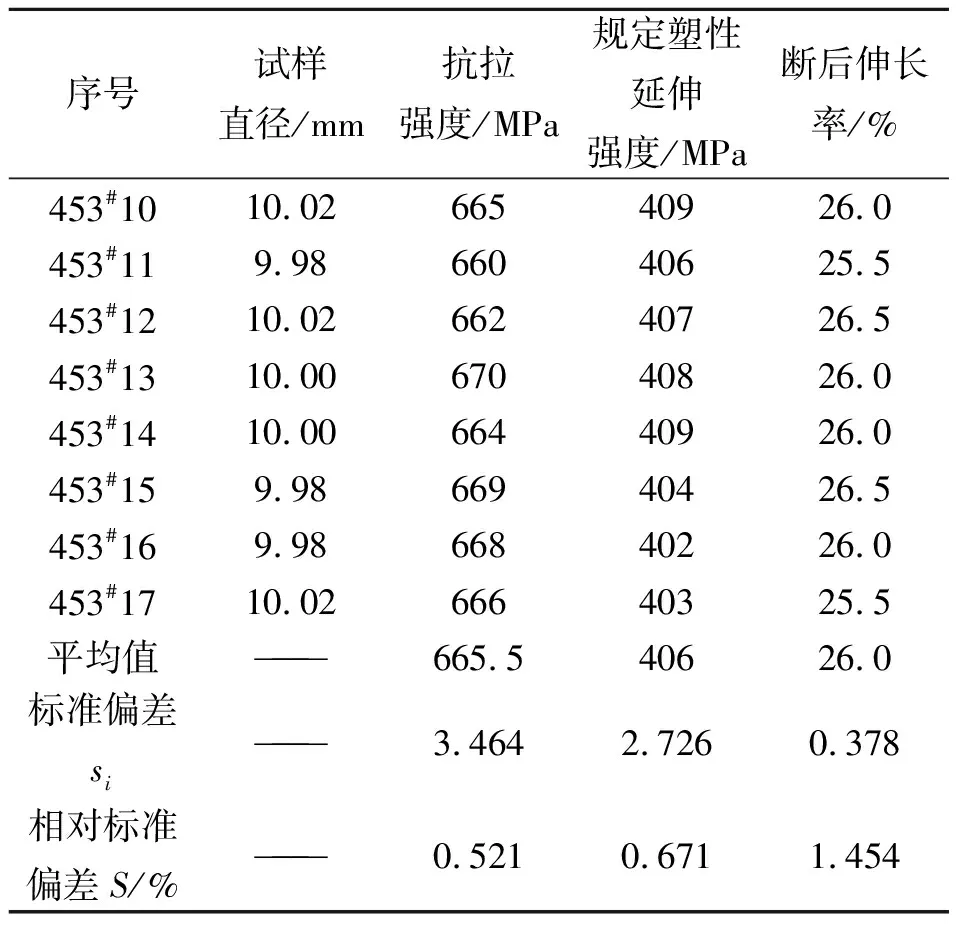
表1 拉伸试验测量结果

试验标准偏差si按贝塞尔公式[2]计算

2 不确定度的评定

2.1 抗拉强度

2.1.1 A类相对标准不确定度urel(rep)的评定

评定单值试样的不确定度为

urel(rep)=S

A类相对标准不确定度如表2所示。

表2 A类相对标准不确定度

2.1.2 最大力Fm的B类相对标准不确定度urel(Fm)的评定

1)试验机测力系统示值误差的相对标准不确定度urel(F1)

使用1.0级拉力试验机示值误差为±1.0%，则

2)标准测力仪检定试验机的相对标准不确定度urel(F2)

依据试验机检定证书(20162017623001-001)，50 kN重复性R=0.1%，可以看成重复性极限，则

urel(F2)=0.058%

3)计算机数据采集系统引入的B类相对标准不确定度urel(F3)

urel(F3)=0.2%

4)最大力的B类相对标准不确定度urel(Fm)

0.612%

2.1.3 试样横截面积S0的相对标准不确定度urel(S0)

测量试样横截面积时，每个尺寸准确到±0.2%。

urel(S0)=2×urel(d)=0.346%

2.1.4 拉伸速率影响带来的相对标准不确定度urel(Rmv)

试验得出，在拉伸速率变化范围内抗拉强度最大相差10 MPa，拉伸速率对抗拉强度的影响为±5 MPa，则

2.1.5 抗拉强度的相对合成不确定度

抗拉强度的相对合成不确定度如表3所示。

表3 抗拉强度的相对标准不确定度分项汇总

相对合成不确定度

ucrel(Rm)=

0.980%

2.1.6 抗拉强度的相对扩展不确定度

取包含概率p=95%，k=2[3]；则

Urel(Rm)=k×urel(Rm)=1.96%

2.2 规定塑性延伸强度不确定度的评定

2.2.1 单值A类相对标准不确定度urel(rep)的评定

urel(rep)=0.671%

2.2.2 规定塑性延伸力的相对不确定度urel(Fp)的评定

使用0.5级引伸计的相对误差为±0.5%，按均匀分布，则

其他B类相对标准不确定度分量的评定与最大力的不确定度分量评定相同。

urel(Fp)=

0.678%

2.2.3 试样横截面积S0的相对标准不确定度urel(S0)

urel(S0)=0.346%

2.2.4 拉伸速率影响带来的相对标准不确定度urel(Rpv)

试验得出，在拉伸速率变化范围内规定塑性延伸强度最大相差7 MPa，拉伸速率对规定塑性延伸强度的影响为±3.5 MPa，按均匀分布，则：

2.2.5 规定塑性延伸强度的相对合成不确定度

规定塑性延伸强度的相对合成不确定度如表4所示。

表4 规定塑性延伸强度的相对标准不确定度分项汇总

相对合成不确定度

ucrel(Rp)=

1.13%

2.2.6 规定塑性延伸强度的相对扩展不确定度

取包含概率p=95%，k=2；则

Urel(Rp)=k×urel(Rp)=2.26%

2.3 断后伸长率不确定度评定

2.3.1 单值A类相对标准不确定度urel(rep)的评定

urel(rep)=1.454%

2.3.2 原始标距的相对标准不确定度urel(L0)的评定

原始标距的标记应准确到±1.0%，则

2.3.3 断后伸长率的相对标准不确定度的评定

断后伸长率的测量应准确到±0.25 mm，本次试验的平均伸长为13 mm；按均匀分布, 则

2.3.4 修约带来的相对标准不确定度urel(off)

断后伸长率的修约间隔为0.5%，则

2.3.5 断后伸长率的相对合成不确定度

断后伸长率的相对合成不确定度如表5所示。

表5 断后伸长率的相对标准不确定度分项汇总

相对合成不确定度

ucrel(A)=

1.997%

2.3.6 断后伸长率的相对扩展不确定度

取包含概率p=95%，k=2；则

Ucrel(A)=k×ucrel(A)=4.0%

2.4 相对扩展不确定度结果汇总

相对扩展不确定度如表6所示。

表6 相对扩展不确定度汇总/%

3 结束语

通过上述评定，可以看出建立正确的数学模型将会对后续的不确定度评定起指导性的作用。建立正确的数学模型，根据数学模型中的各种参数，分别分析可能对这些参数产生影响的主要不确定度来源，并对这些不确定度来源的分量进行评定并合成，最后对数学模型中的所有参数的不确定度分量以及A类(统计类)不确定度分量进行合成，从而计算出该项目在包含概率p=95%下的不确定度，为金属材料棒状试样拉伸试验不确定度提供有效的评定方法。