利用成长模型的自适应垂直坐标序列分析

王梦婷 ,聂建亮,郭春喜,田 婕,王 斌

(1.西安建筑科技大学 理学院 陕西 西安 710055 2.国家测绘地理信息局 大地测量数据处理中心,陕西 西安 710054)

地面沉降是近几十年世界各国普遍发生的地质灾害，对当地人们生活与经济建设造成了巨大的损失.地面沉降点垂直运动轨迹随时间要经过发生、发展、成熟、稳定4个阶段，运动轨迹一般呈S曲线形式，常速度,常加速度等物理运动模型虽然能够预报较短时间的平稳载体运动状态，但并未考虑地质等因素影响，所以长时间预报精度可能不高.地质学者常利用Weibull等成长模型描述地面沉降过程，充分考虑沉降区域地质条件与水文因素，利用最小二乘等拟合方法整体计算成长模型参数，有效反演软地基等地面沉降全过程；考虑到Gompertz模型与Logistic模型需要足够的施工期或S曲线反弯点以前的沉降观测样本，S曲线反转点沉降值与最终沉降相对不变，Weibull成长模型克服了Gompertz模型与Logistic模型的缺陷，削弱了实测样本对反弯点的依赖，提高了地面沉降的预报精度[1-3].成长模型作为地面沉降预报模型，能够改善滤波在地面沉降预报中的地质背景基础，提高滤波解的估计精度，给出合理的地面沉降机理诠释.另外由于数据处理策略、卫星轨道、环境因素等影响，垂向坐标序列中存在季节性、非季节性的有色噪声，国内外学者采用误差模型改正与自适应滤波方法削弱有色噪声影响[4-6].如Dong等计算了水体、大气等质量负荷造成的地壳弹性变形[5-7]；杨元喜等学者提出了自适应滤波算法，构造自适应因子调整预测值协方差矩阵与观测噪声协方差矩阵的比例关系，提高滤波解的可靠性[8-10].鉴于以上研究基础，提出基于地面沉降成长模型的自适应滤波算法，利用成长模型作为滤波动力学模型，采用预测残差构造自适应因子，实时调整状态方程与观测方程的比例关系，进一步提高地面沉降监测点的滤波解精度.

1 动力学模型

目前，Kalman滤波的动力学模型有常速度(CV)模型、常加速(CA)模型、一阶时间相关(Singer)模型和“当前”统计模型等多种构造形式[10-11].对于变化缓慢的地面沉降监测点的垂直运动，常速度、常加速等模型不能较好地描绘地面沉降长期运动规律，而Gompertz、Logistic、Weibull成长模型是地质学者预测地面沉降全过程的常用模型，能够更真实地反映监测点的垂直运动曲线[1-3].

1.1 成长模型

Gompertz、Logistic成长模型虽能反映监测的总体S形沉降过程，在反弯点处与最终沉降的比值为常数，另外这两个模型要求在沉降开始阶段或S反弯点前需要大量的观测样本.而Weibull成长模型能够克服Gompertz、Logistic成长模型的不足，能够真实反映监测点的瞬时垂直方向的有界变化.

Gompertz成长模型为[1]

x(t)=aexp[-hexp(-bt)]

(1)

其中：a、b、h为待定参数；t为时间.

Logistic成长模型为

(2)

其中，a、b、h为待定参数，且均为非负.

Weibull成长模型为

x(t)=a-(a-b)exp[-(ht)c]

(3)

式中，a、b、c、h为待定参数，a为最终沉降量，b为初始沉降量，h为地基加荷因子，c为综合影响因子，且a、b、h非负.当a>b时，c>0，反之，c<0.

1.2 滤波动力学模型

考虑沉降点加速度数值较小，将加速度作为不变值.则第k历元的Weibull成长模型向量表示简化为

(4)

预报值对应协方差矩阵为

(5)

其中，ΣWk计算可以参考文献[10-11].

2 自适应因子构造

地面沉降监测点一般垂直运动较缓慢，多类因素影响导致运动具有不确定性.Weibull成长模型能够较可靠地描述地面沉降监测点的运动状态，提高自适应滤波动力学模型的预测值的精度.考虑垂直运动为一维运动，而待估参数为位置、速度、加速度，最小二乘方法单历元秩亏，无法利用状态不符值构造自适应因子的误差统计量.因此，根据预测残差构造模型误差统计量[2,8]

(6)

其中，tr(·)表示迹.

位置的自适应因子采用两段函数构造[10,12].

(7)

式中，k0为阈值，一般取值3.0～8.5.

而速度、加速度为间接可测参数[13]，无法通过观测方程获得估计值，此处，自适应因子都取1.0.

3 基于成长模型的自适应滤波

第k历元自适应Kalman滤波解为[10]

(8)

(9)

其中，αk为自适应因子矩阵， 即

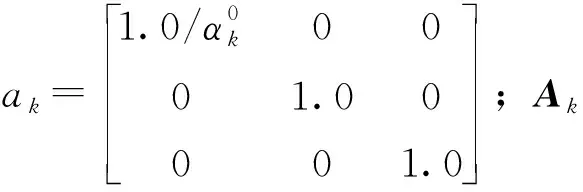
第k历元自适应Kalman滤波残差为

(10)

4 算例分析

山东省西北部与黄河三角洲是地面沉降严重区域，目前德州、广饶、齐河地区沉降严重，造成了巨大的经济损失.算例采用沉降严重区域德州(DEZH)、广饶(GURA)、齐河(QHRS)连续运行参考站的2010～2015年垂向坐标序列验证自适应滤波的可靠性，其中数据采样间隔为1d.在计算过程中，首先利用最小二乘方法获得这些测站的年周期、半年周期等周期项参数，并在垂向坐标序列中扣除其影响；利用垂向坐标序列获得成长模型参数；最终利用自适应滤波处理“干净”的垂向坐标序列，自适应因子采用预测残差构造误差统计量.另外速度谱密度取10-3cm2/s2，观测值协方差为10-3cm2.算例采用9种方案：

方案1：Gompertz成长模型；

方案2：标准Kalman滤波，动力学模型采用Gompertz成长模型；

方案3：自适应Kalman滤波，动力学模型采用Gompertz成长模型；

方案4：Logistic成长模型；

方案5：标准Kalman滤波，动力学模型采用Logistic成长模型；

方案6：自适应Kalman滤波，动力学模型采用Logistic成长模型；

方案7：Weibull成长模型；

方案8：标准Kalman滤波，动力学模型采用Weibull成长模型；

方案9：自适应Kalman滤波，动力学模型采用Weibull成长模型.

统计三个连续运行参考站的不同方案残差序列，得到各方案RMS，统计于表1，各方案误差曲线绘于图1—图9.

(11)

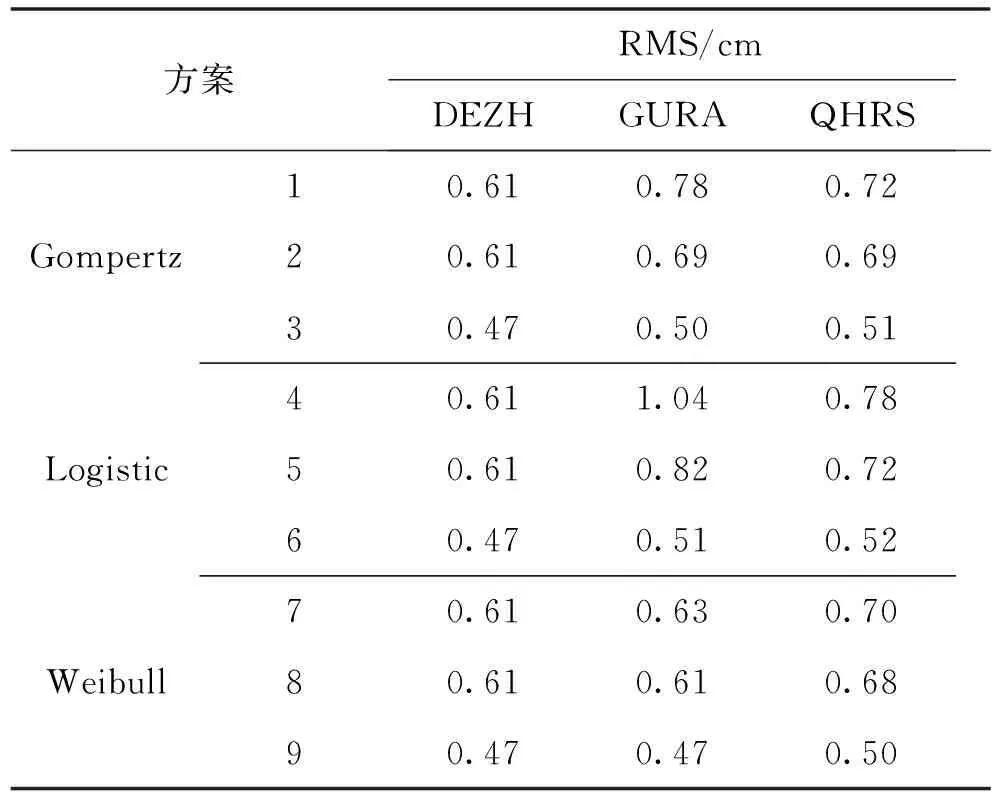
表1 各方案RMS统计结果Tab.1 The error statistics of the coordinate components

由以上计算结果可以看出：

(1)广饶、德州、齐河站的地面沉降灾害基本上处于成长、成熟阶段，Gompertz、Logistic、Weibull成长模型都能够反映这三个连续运行站的垂直运动规律，Weibull成长模型预报精度优于Gompertz、Logistic成长模型.

(2)与方案1、4、7相比，方案2、5、8精度有一定程度提高.这是因为在成长模型作为预报模型基础上，Kalman滤波利用观测信息，进一步修正预报值结果，提高滤波解的可靠性.

(3)三个站的自适应滤波与成长模型相比，精度平均提高约30%，最大提高幅度51%；三个站的自适应滤波与标准Kalman滤波相比，精度平均提高约25%，最大提高幅度38%.这是因为根据预测残差构造误差统计量，采用两段函数构造自适应因子，利用自适应因子合理调整Kalman滤波的动力学模型与观测值对滤波解的贡献，进一步提高滤波解的精度与可靠性.

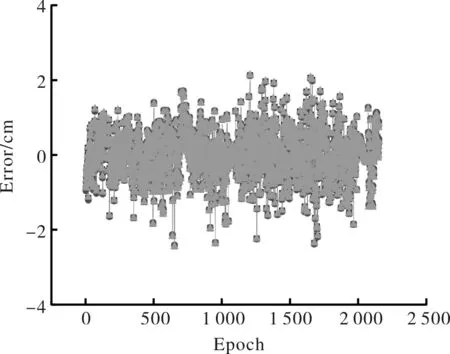
图1 德州站地面沉降成长模型误差曲线Fig.1 The error of grown models in DEZH

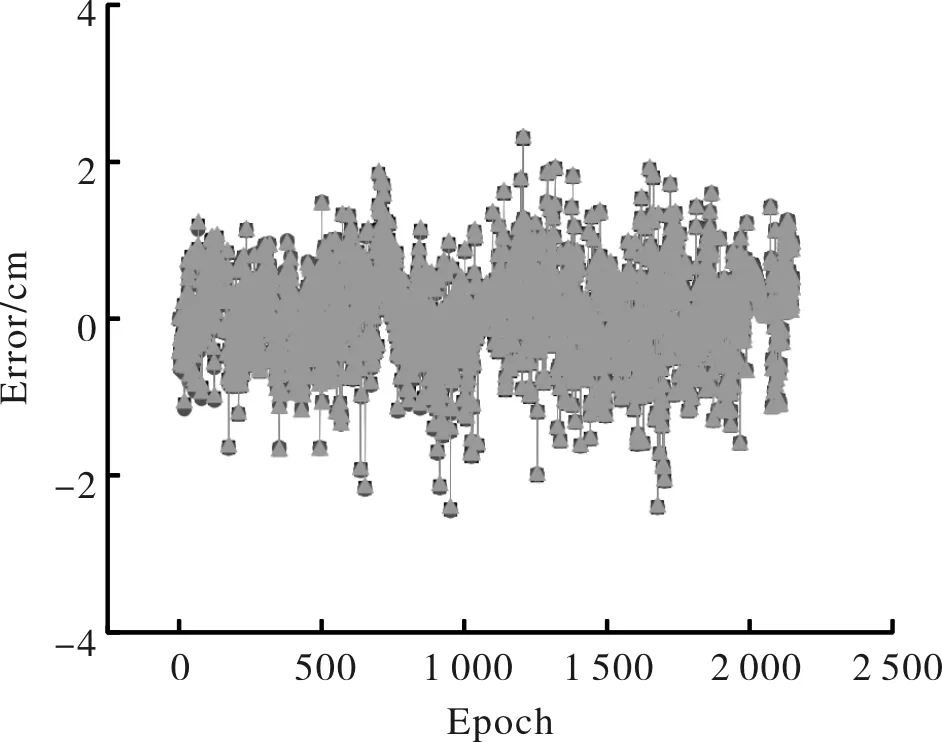
图2 德州站标准Kalman滤波误差曲线Fig.2 The error of Kalman filtering in

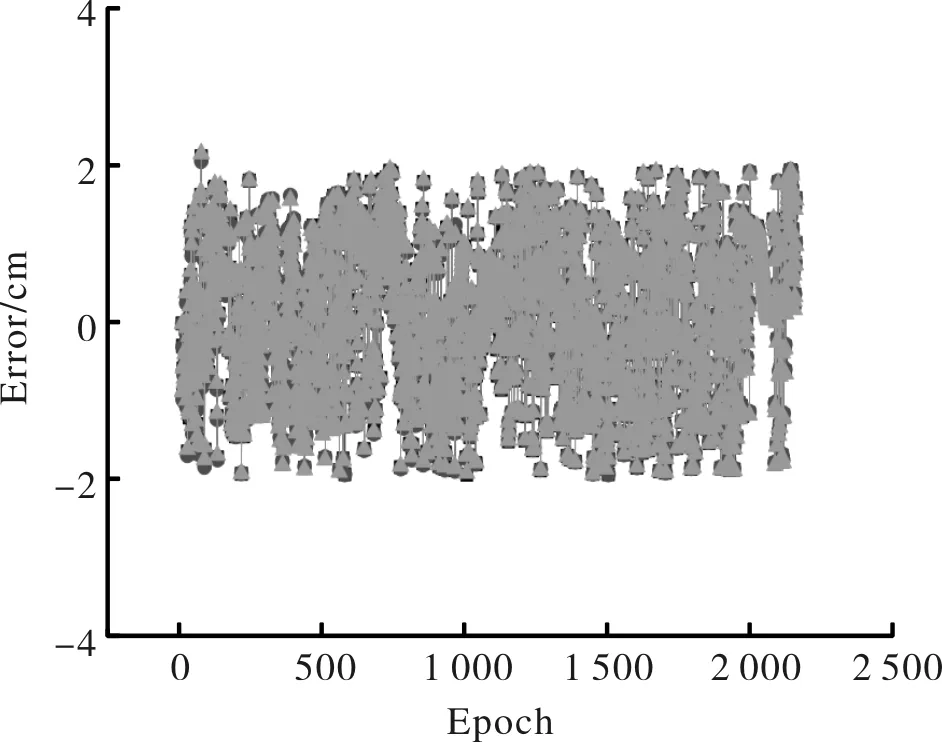
图3 德州站自适应Kalman滤波误差曲线Fig.3 The error of adaptive Kalman filtering in

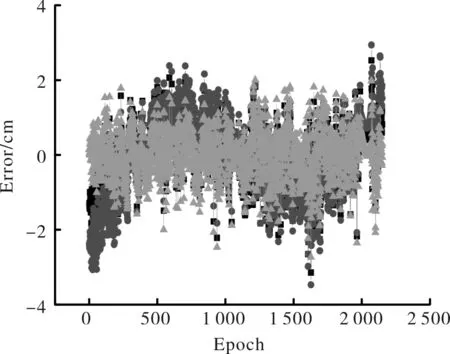
图4 广饶站地面沉降成长模型误差曲线Fig.4 The error of grown models in DEZH

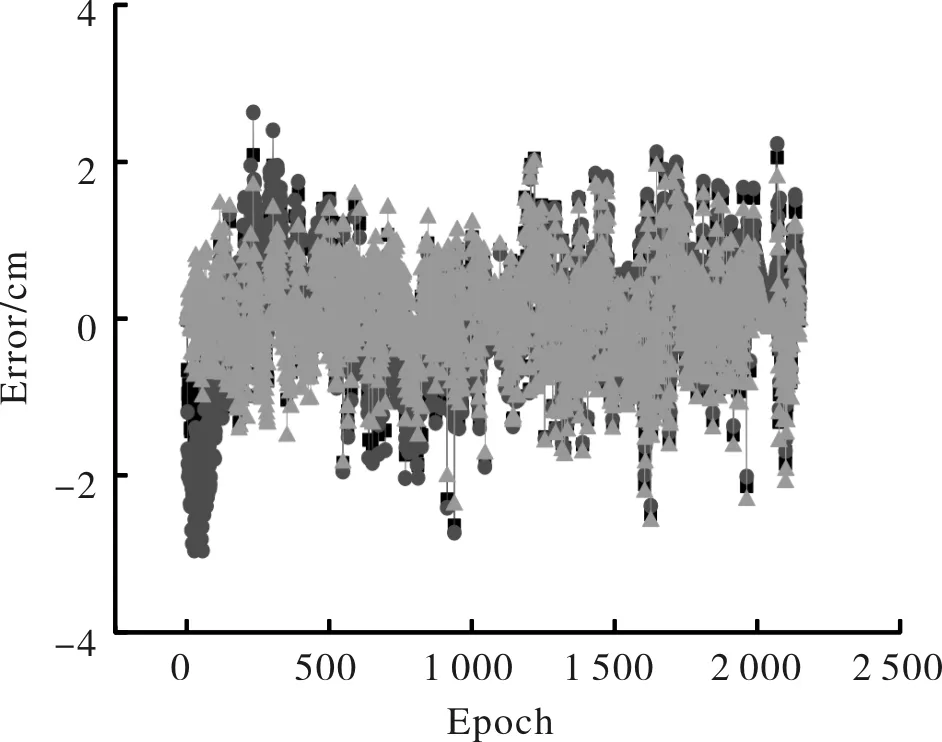
图5 广饶站标准Kalman滤波误差曲线Fig.5 The error of Kalman filtering in GURA

图6 广饶站自适应Kalman滤波误差曲线Fig.6 The error of adaptive Kalman filtering in GURA

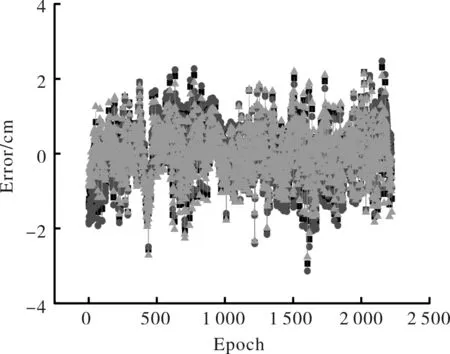
图7 齐河站地面沉降成长模型误差曲线Fig.7 The error of grown models in DEZH

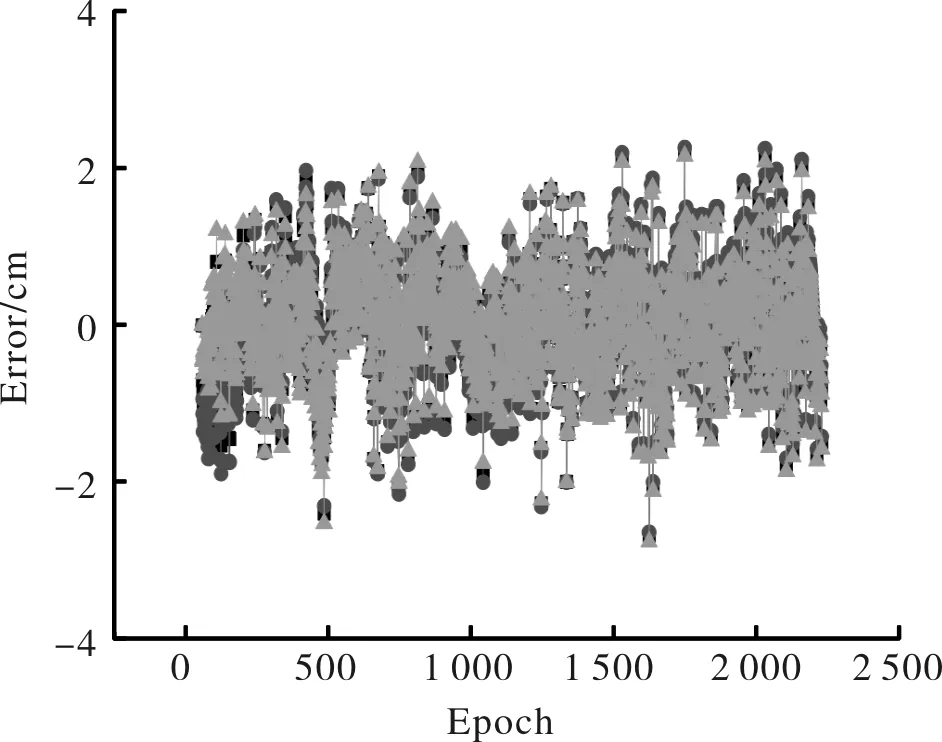
图8 齐河站标准Kalman滤波误差曲线Fig.8 The error of Kalman filtering in QHRS

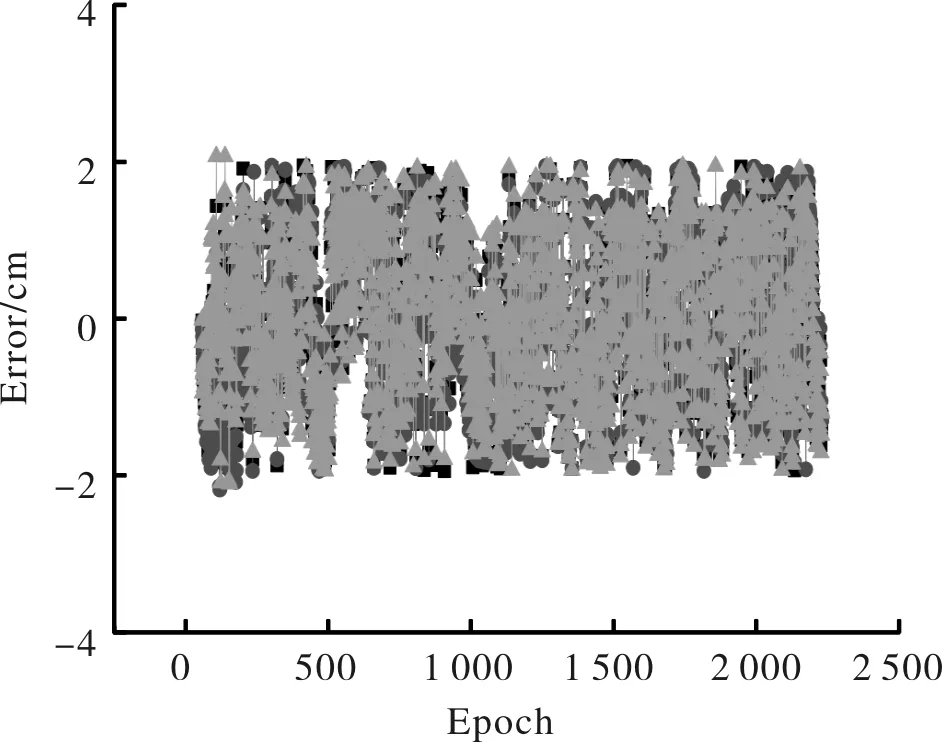
图9 齐河站自适应Kalman滤波误差曲线Fig9 The error of adaptive Kalman filtering in QHRS

5 结语

连续运行参考站在地面沉降中发挥着不可替代作用，实时监测地面点的垂直运动变化.地面沉降成长模型能够有效描述连续运行参考站的沉降全过程；而Kalman滤波将地面沉降成长模型作为动力学模型，能够提高地面点垂直运动的可靠性；自适应Kalman滤波利用自适应因子调整动力学模型与观测值之间的关系，进一步提高地面沉降监测点垂直坐标序列的自适应滤波解精度.另外，地面沉降点受季节等因素影响，垂直坐标序列中存在有色噪声，这削弱了常用滤波估计结果的精度，降低了地面沉降速度的可靠性.因此，研究坐标序列的有色噪声成分及误差改正模型是下一步的工作.

致谢：感谢山东国土测绘院与陆态网络中心提供的试验观测数据.