基于交替方向乘子法的图像复原问题研究

杨静雅

(长治学院 数学系,山西 长治 046011)

0 引言

图像处理中的图像复原问题早在1960年就被提出[1]．在图像复原问题中,原图像记为x,观测到的图像记为y,观测图像通常会受到噪声的影响,建立模型如下:

y=Bx+n,

(1)

其中B为矩阵,表示直接作用的算子,n为噪声项．通常,将图像进行取样和量化,得到的结果是实数矩阵．在一般的图像复原问题中,B表示线性作用算子．复原处理有时也称为反卷积,则矩阵B表示一个卷积算子．由于相机与被摄物体之间可能存在相对运动,造成运动模糊、聚焦偏差等,即为模型中的噪声项,会对观测结果产生一定的影响．

1 无约束优化问题

约束优化问题的一般形式:

(2)

其中ε为常数且ε≥0,φ(x)是光滑或者非光滑的目标函数．当φ(x)=‖x‖1,ε=0时,上述问题通常称为基追踪问题．

最近几年,根据(2)式提出了压缩感知问题[2,3]．基于矩阵B和原始图像x的稀疏程度,压缩感知的相关理论提供了(2)式解的条件．在大多数的压缩感知和图像复原问题中,非光滑的正则项,例如:全变差、l1范数,是较为常见的形式[2,4]．

针对无约束优化问题,即

(3)

其中,τ称为正则化参数．显然,问题(3)和(2)是等价的．为了解决问题(3),提出了一些基于迭代收缩的算法,例如:加速方法SpaRSA[5]、迭代方法TwIST[6]和FISTA[7]等．大多数这些算法的关键因素是收缩、阈值,以及去噪功能．基于以上特点,得到函数:

(4)

针对目标函数是两个函数之和的无约束优化问题,形式如下:

(5)

其中g:Rn→Rd．

采用分离变量法,创建一个新的变量v,满足v=g(u),作为f2的变量,即

(6)

通过引入二次惩罚项的方法,将问题(6)转化为无约束优化问题,即

(7)

通过交替进行,化u和v为最小值,当α取值很大时,(7)式可逼近(6)式,同时,也与(5)式等价．

对于图像复原的无约束优化问题,如(3)式中的定义．这个问题可以写成如下形式:

f2(x)=τφ(x).

(8)

则得到相应的约束优化问题:

s.t.x=v.

(9)

如果φ(x)=ψ(Dx),利用分离变量法,得到下面的约束优化问题:

(10)

2 提出的算法

2.1 采用对称形式的交替方向乘子法,原理如下:

minf(x)+g(z) s.t.Ax+Bz=c.

(11)

其对应的拉格朗日表达式为:

(12)

对称形式的交替方向乘子法,包括以下迭代步骤:

yk+1/2=yk+ρ(Axk+1+Bzk-c)

(13)

yk+1=yk+1/2+ρ(Axk+1+Bzk+1-c),

(14)

那么上面的迭代步骤可以变为以下形式:

uk+1/2=uk+Axk+1+Bzk-c

(15)

uk+1=uk+1/2+Axk+1+Bzk+1-c

这种交替化求最小的方法,与原来的无约束问题(5)相比,每一步的运算更容易求解．

2.2 对称的交替方向乘子法——SUMAM,算法如下:

算法SUMAM

1)k=0,取μ=0.9,选择v0和λ0;

2)重复;

4)λk+1/2=λk-(xk+1-vk);

6)λk+1=λk+1/2-(xk+1-vk+1);

7)λ←λ+1;

8)满足某个终止规则,停止．

其中,对算法中第三步骤的式子求解,得到解的形式如下:

(16)

对算法中第五步的式子求解,得到的解如下:

(17)

3 数值实验

考虑关于摄影师图像的修复问题,摄影师的原始图像及观察到的图像如下图所示,其中,观测图像(图2)被高斯噪声(SNR值为40 dB)破坏,与原始图像相比,缺失了40%的像素．

图1 原图

图2 噪声污染的图像

图3 修复后的图像

算法迭代次数CPU/sSUMAM7412.9TwIST502143FISTA50088.4

利用SUMAM算法编程,通过Matlab软件对图2进行处理,得到结果如图3所示,与图1进行对比,清晰度较高,达到了非常好的修复效果．

表1给出了SUMAM算法与TwIST算法、FISTA算法处理上述问题时,在迭代次数与CPU运行时间的比较．

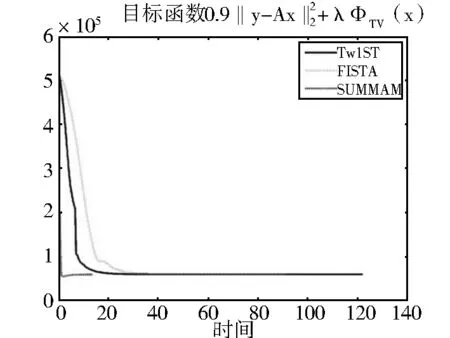
图4 三个算法的比较

图4表示利用SUMAM算法与TwIST算法、FISTA算法处理上述问题时,三种算法各自的目标函数随时间的变化情况．

本文所有实验均在Matlab R2008a,win7系统,处理器AMD Athlon(tm) II×2 215,CPU 2.70 GHz,RAM:2.00GB环境下运行．

4 结论

本文针对一类无约束优化问题,利用对称形式的交替方向乘子法SUMAM进行求解．数值实验结果表明,该算法达到了较好的修复效果．特别是,该算法迭代次数以及CPU均大幅度减少,较大程度上提高了运算效率,验证了算法的可行性以及在修复速度方面的优势．