Toeplitz矩阵填充的中值修正的奇异值阈值算法
2018-12-06牛建华王川龙
牛建华,王川龙
(太原师范学院 数学系,山西 晋中 030619)
0 引言
矩阵填充问题近几年发展迅速,它主要研究的是根据采样矩阵的部分已知元素合理精确地填充一个低秩矩阵,著名的Netflix推荐系统[1]就是一个经典的应用. 该问题可以通过如下模型解决
minrank(X)
(1)
s.t.Xij=Mij(i.j)∈Ω.
其中X,M∈Rn1×n2,并且M表示采样矩阵,Ω∈{1,…,n1}×{1,…,n2}表示采样矩阵已知元素的下标集合.事实上,由于矩阵关于秩是不连续的,所以模型(1)解决此问题存在一定的困难,所以Cand′es和Recht[2]提出模型(1)可以转化为如下凸优化问题:
min ‖X*‖
(2)
s.t.Xij=Mij(i.j)∈Ω.

此外,,Qiao等人[15]根据Lanczos方法和FFT技术提出的Hankel矩阵的奇异值分解算法其复杂度为O(n2logn),但是一般矩阵的复杂度为O(n3),并且Toeplitz矩阵可以通过行列变换转化为Hankel矩阵,因为计算奇异值分解时间在整个矩阵填充中所占比例很大,所以新算法在时间上占一定的优势.
为了方便,我们先来给出一些定义.
定义1 一个n×n的Toeplitz矩阵T∈Rn1×n2有如下形式:
显然,Toeplitz矩阵是由其第一行和第一列共2n-1个元素决定.
定义2([16]) (奇异值分解(SVD)). 秩为r的矩阵X∈Rn1×n2,一定存在正交矩阵U∈Rn1×r和V∈Rn2×r,满足
其中σ1≥σ2≥…≥σr>0.
定义3([3]) (奇异值阈值算子). 对于任意参数τ≥0,矩阵的秩是r,X∈Rn1×n2,则存在X=UΣrVT,奇异值阈值算子Dτ定义为
Dτ(X)=UDτ(Σ)VT,Dτ(Σ)=diag({σi-τ}+)
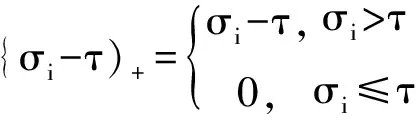
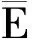
并且令
1 算法
在本节中,我们提出了Toeplitz矩阵填充的一种新算法,上述问题可以转化为如下凸优化模型
min ‖X‖*
(3)
s.t.PΩ(X)=PΩ(M)
其中X,M均是Toeplitz矩阵,Ω∈{-n+1,…,n-1}. 并且为了方便,用[Uk,Σk,Vk]τk=lansvd(Yk)表示对矩阵Yk进行奇异值分解.
算法1(Mid-SVT算法)
第一步:给定下标集合Ω,样本矩阵PΩ(M),参数τ0,0 第二步:计算矩阵(Yk)的奇异值 [Uk,Σk,Vk]τk=lansvd(Yk). 表1 算法Mid-SVT和算法ALM算法的比较结果(p=0.1) 表2 算法Mid-SVT和算法ALM算法的比较结果(p=0.2) 表3 算法Mid-SVT和算法ALM算法的比较结果(p=0.3) 表4 算法Mid-SVT和算法ALM算法的比较结果(p=0.4) 注:由于采样矩阵M随机产生Toeplitz矩阵PΩ(M),其位置元素的位置不同,因此,个别实验的数据有所波动. 在本文中,我们提出了Toeplitz矩阵填充的一种新算法——中值修正算法,根据表1-表4数据,我们可以看出新算法在填充总时间、最终误差等方面都比ALM算法优势明显,尤其是当p=0.1,p=0.2的时候,ALM算法收敛效果不理想,而新算法有较好的收敛性. 此外,从整体上看,随着采样率p的增大,计算时间越少,这也是合理的.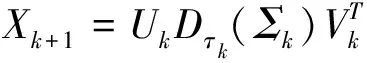
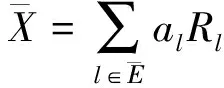
2 数值结果
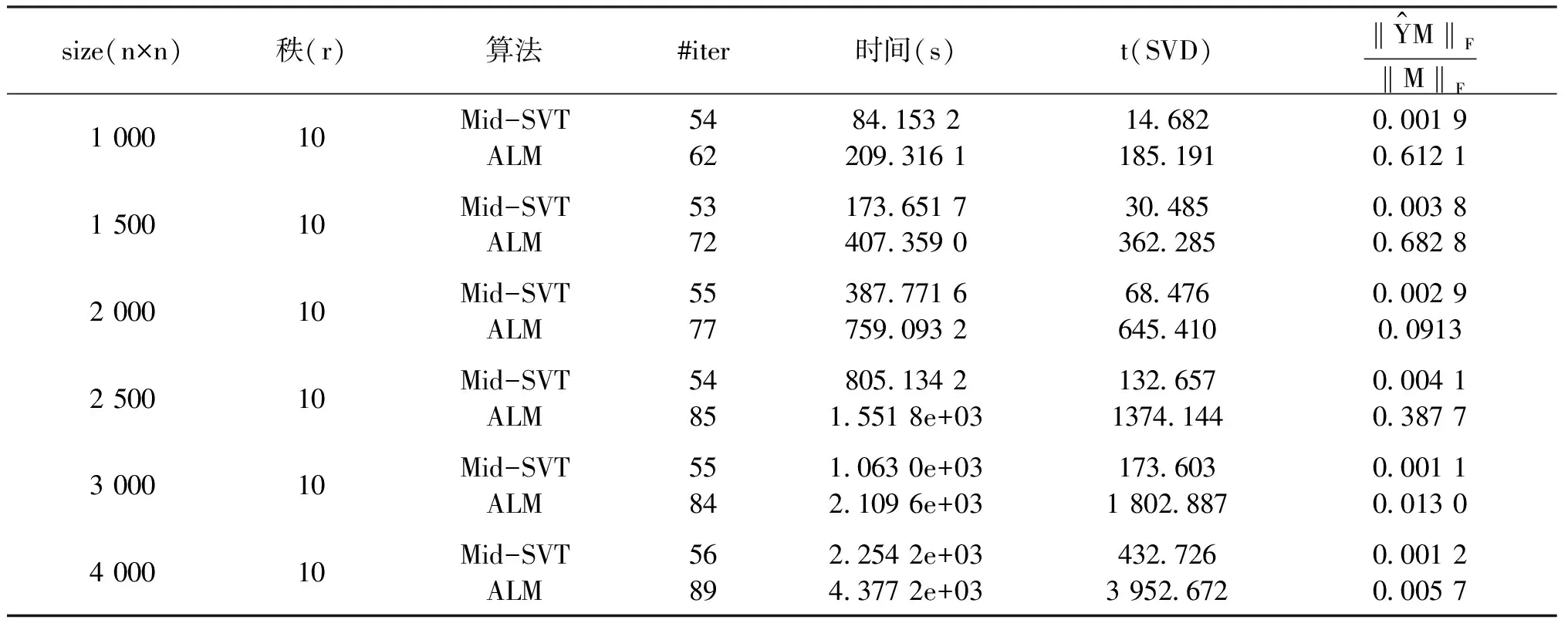
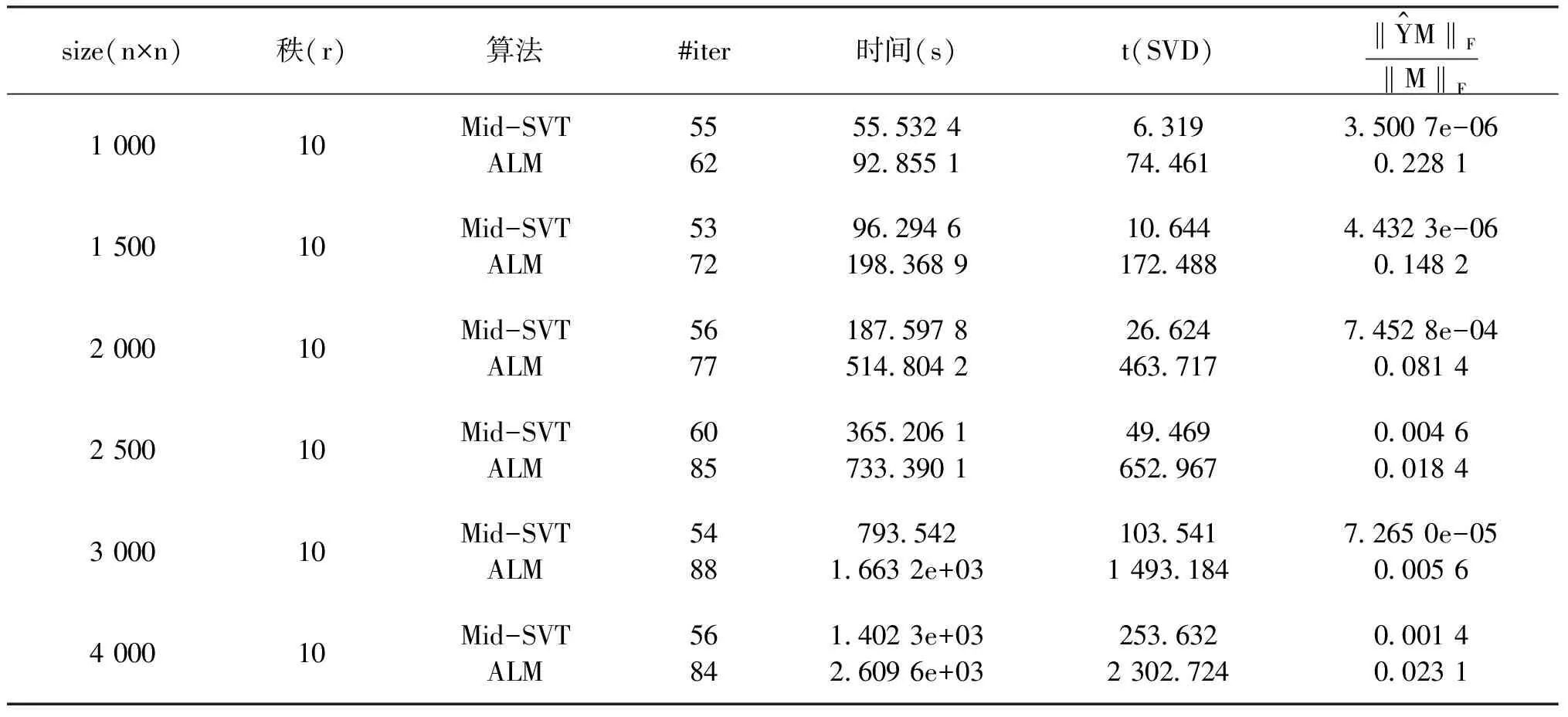
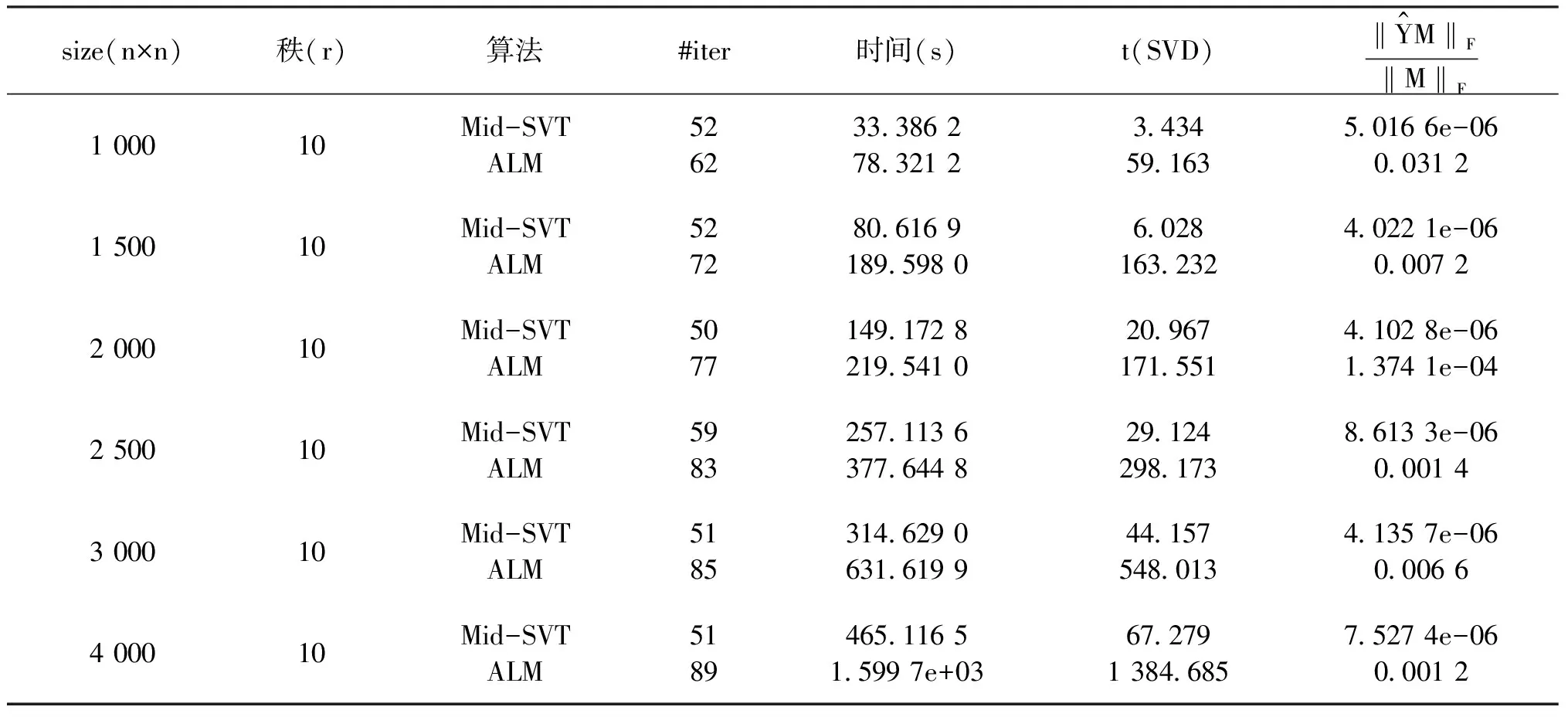
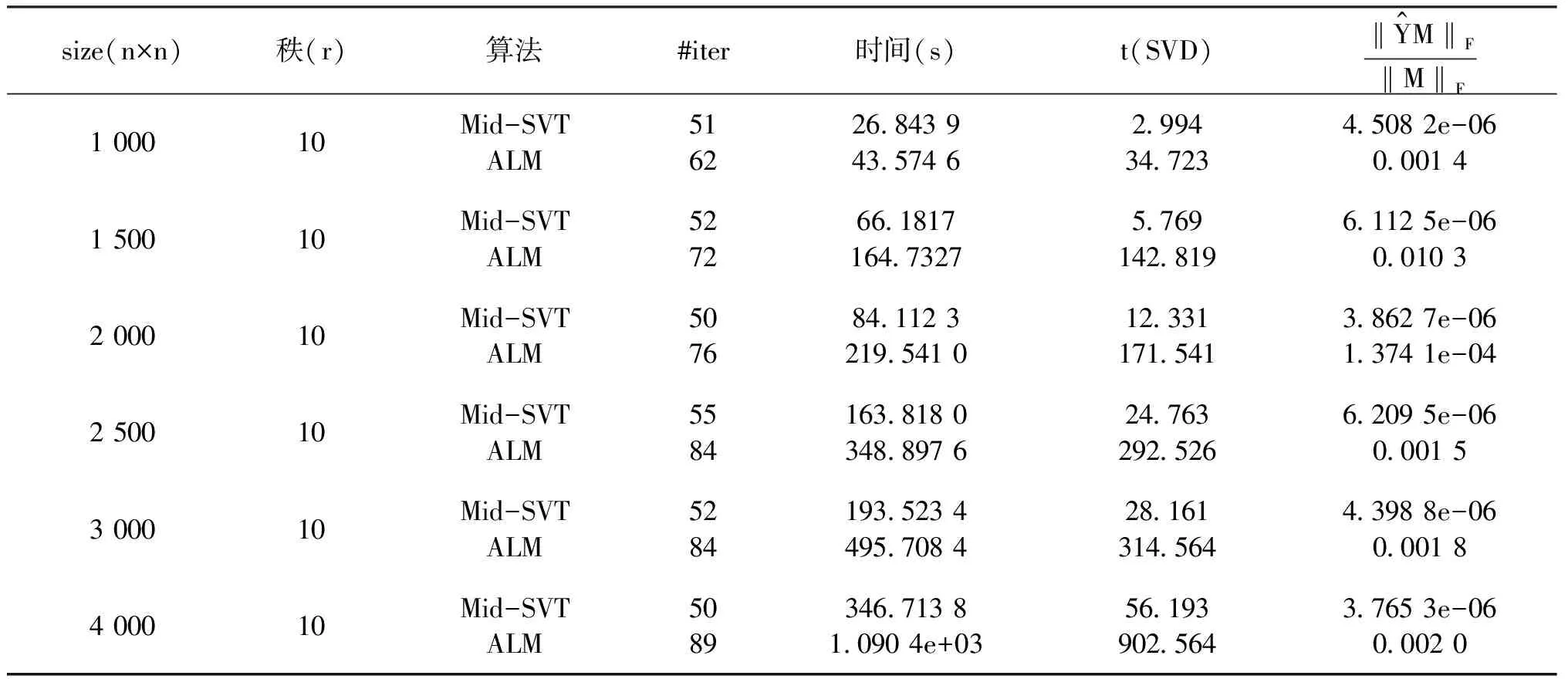
3 总结
