基于响应面法的钢-砼混合梁悬索桥有限元模型修正

石帅 李永红

（1 中南林业科技大学土木工程学院，湖南 长沙 410004；2 中南林业科技大学工程流变学湖南省重点实验室，湖南 长沙 410004）

1 引言

有限元模型修正技术是基于静动载试验结果，修改初始有限元模型的物理及几何尺寸等参数，使得优化调整后的有限元模型计算结果与试验实测值接近。响应面修正方法是一种能够将复杂的输入变量与输出响应的关系建立成某个显式关系的方法[1]。

2 有限元模型的建立与荷载试验

某悬索桥主梁为钢-砼混合梁，两边边跨都是108.85m混凝土箱梁，中跨是280m钢箱梁，索塔高74.5m，主缆中心线最低标高29.3m，主缆垂跨比1/6。作者采用Midas Civil桥梁结构通用有限元分析与设计软件进行桥梁建模，有限元模型见图1。

图1 有限元模型

对桥梁进行荷载试验，利用加载车对桥梁进行两次静载试验，测得工况1与工况2的13个测点D1～D13的竖向位移。进行脉动试验，采用高灵敏度的拾振器和放大器测量结构在环境激励下的振动，测得前三阶结构自振频率ω1、ω2、ω3。

3 基于响应面法的有限元模型修正

3.1 修正参数选取与显著性检验

根据工程经验，初步选定8个修正参数分为别：混凝土箱梁、钢箱梁、主缆、吊杆的弹性模量及其质量密度，记为E1、E2、E3、E4、ρ1、ρ2、ρ3、ρ4。选用均匀设计方法进行试验设计，然后调用有限元模型进行计算。通过F检验法分析各参数对响应的显著性，其中P值是进行检验决策的一个依据。在给定显著水平α=0.05的情况下，若P≤=α0.05，则认为模型的这个变量对响应的影响显著；若P＞=α0.05，则不显著。各参数P值见图2。由图可知，D1、D2、D3、D11、D12、D13混凝土箱梁上的 6个位移测点，混凝土弹性模量E1对其影响显著，其P值皆小于0.05。D4～ D10钢箱梁上的7个位移测点，混凝土弹性模量E1、钢箱梁弹性模量E2及主缆弹性模量E3的影响显著，P值皆小于0.05。ω1、ω2、ω3三阶自振频率则是钢箱梁弹性模量E2、主缆弹性模量E3及钢箱梁的质量密度ρ2对其影响显著，故选用E1、E2、E3修正位移，选用E2、E3、ρ2修正频率。

图2 各参数对响应的P值

3.2 响应面拟合与验证

响应面模型有很多种，常见的有多项式函数、幂函数、径向基函数等[3]。多项式函数拟合方法是响应面建模使用最广泛的一种方法。一阶、二阶完全多项式模型见式（1）与式（2）。

选定修正系数后，对有限元模型计算结果进行拟合，得到代替有限元模型的响应面函数模型，一阶完全多项式响应面函数各参数的系数见表1，二阶完全多项式响应面函数各参数的系数限于篇幅未列出。

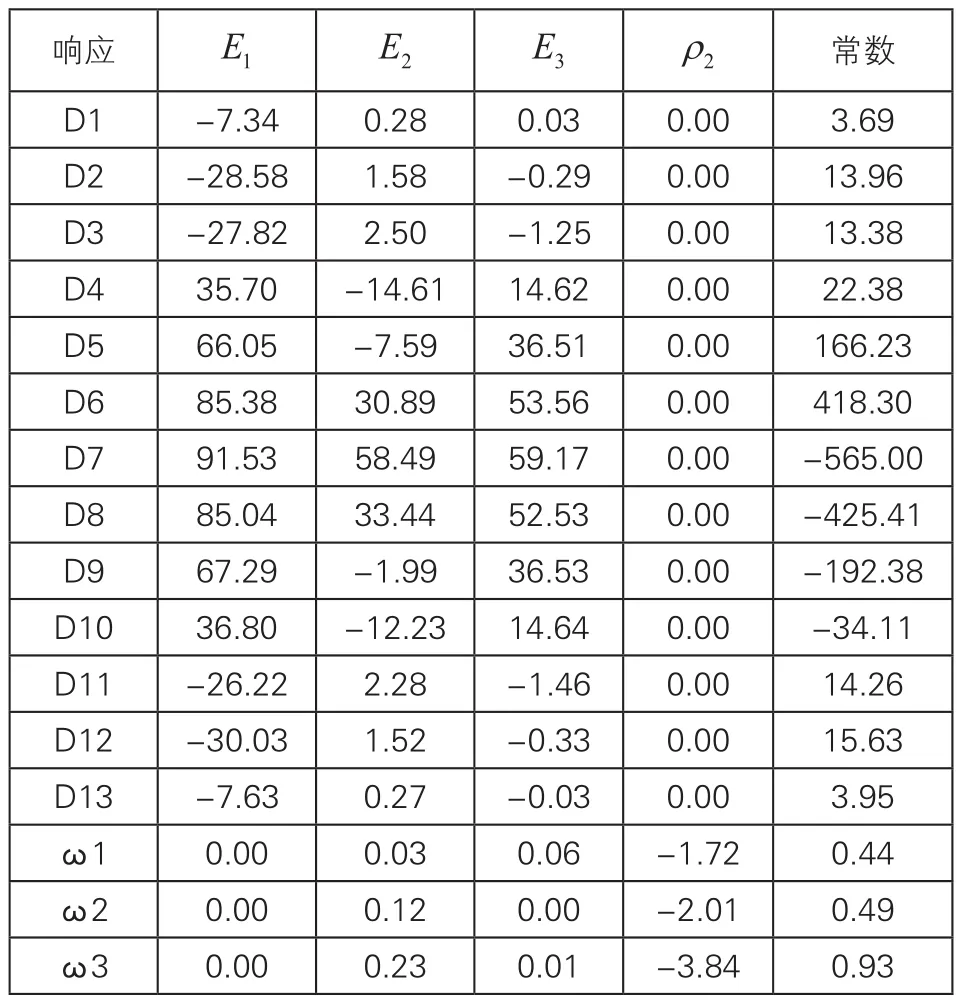
表1 一阶响应面函数各参数的系数

响应面的优劣将直接影响优化的结果，最终影响有限元模型修正的效果[4]。检验的指标一般有多重判定系数R2及标准误差。拟合的各响应面函数的R2值介于0.98685～0.99999之间，R2值都很接近于1，说明拟合效果理想；标准误差值介于0.00001～0.46709之间，都接近于0，表示函数的预测值与真值误差较小。一、二阶响应面都能较好的反映结构响应与参数之间的关系，可以有效地代替有限元模型用以优化计算。

3.3 目标函数及优化

建立好响应面函数之后，通过响应面函数的计算值与荷载试验实测值之间的差异来构造目标函数F。作者分别建立了基于一阶完全多项式响应面目标函数，见式3；基于二阶完全多项式响应面的目标函数，见式4。

式中D1ai、ω1ai为一阶响应面计算位移与计算频率，D2ai、ω2ai为二阶响应面计算位移与计算频率。Dti、ωti实测位移与实测频率。构造出目标函数，结构有限元模型修正就转化为对优化问题minF（X）的求解。

通过遗传算法、序列二次规划法（SQP）分别求优化问题的最优解，可得目标函数的优化结果，见表2。2个目标函数经过优化后的最优值都很接近于0，且遗传算法与序列二次规划法计算出的结果十分接近，说明优化效果理想。本文仅选用遗传算法修正结果进行误差分析。

表2 目标函数的优化结果

3.4 误差分析

经遗传算法将参数优化后，用修正后的模型计算各响应进行误差分析，见图3。

误差=|计算值-实测值|/实测值。

图3 一阶、二阶响应面修正的响应误差

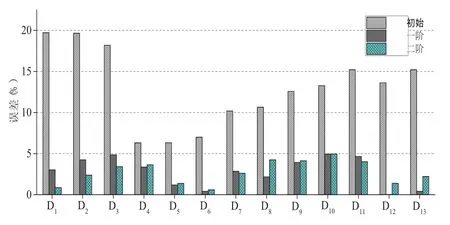
图4 一阶、二阶响应面修正的响应误差（工况2）

由图3，初始有限元模型计算出的初始响应误差较大，大部分位移测点误差大于10%。对于频率，误差在5%～8%之间。基于一阶响应面的修正，竖向位移误差和频率误差都小于5%，满足工程需要。其中D4、D7、D9修正效果最好，皆小于2%。前三阶频率误差都小于2%。基于二阶响应面的修正，竖向位移误差和频率误差都小于5%，其中D3、D4、D7修正效果最优，都小于1%，部分竖向位移误差较一阶修正的结果更小。

为了验证修正的效果，将修正后的模型对工况2进行模拟，并与实测数据进行对比，误差分析见图4。由图可见基于一阶、二阶响应面修正模型后，位移与频率误差皆小于5%。综上，基于一阶、二阶响应面的修正皆符合工程要求。

4 结语

本文基于荷载试验所得静力与动力信息，对某钢-砼混合梁悬索桥进行有限元模型修正，得出以下结论：对于此类桥梁，基于一阶响应面及二阶响应面的修正都具有较好的修正效果。基于响应面的有限元模型修正方法修正精度高，求解效率高。