logistic回归概率模型在物质浓度辨识中的应用

王诚 刘硕

（兰州石化职业技术学院信息处理与控制工程学院，甘肃 兰州730060）

0 引言

比色法是目前常用的一种检测物质浓度的方法，即把待测物质制备成溶液后滴在特定的白色试纸表面，等其充分反应以后获得一张有颜色的试纸，再把该颜色试纸与一个标准比色卡进行对比，就可以确定待测物质的浓度档位了。由于每个人对颜色的敏感差异和观测误差，使得这一方法在精度上受到很大影响。随着照相技术和颜色分辨率的提高，希望建立颜色读数和物质浓度的数学模型，即只要给模型输入照片中的颜色读数就能够通过计算获得待测物质的浓度，而模型的精度直接关系着待测物质浓度的准确性,见于监测数据呈现明显的类状或族状，可以将物质浓度判断问题归结为类别辨误问题或模式识别问题。为此，本文在已知颜色读数和相应物质浓度实验数据的基础上建立了基于logistic回归的物质浓度识别模型，该模型是实质上是一种多元非线性概率回归分析模型，实例分析表明用该模型预测物质浓度具有很高的精确度，好于支持向量机[1-2]、神经网络[3-4]等辨识模型，值得工程技术人员借鉴。

1 logistic回归概率模型

设表征物质浓度的常用颜色有：蓝色B、绿色G、红色R、色调H、饱和度S，其读数分别为x1、x2、x3和x4；对物质浓度进行类别划分，类别值{1,2,…,J}（J为总类别数）；设研究对象（物体）记为X，其样本集X={X1,X2,…,Xn}（Xi为样本，i=1,2,…,n），且Xi=（xi1,xi2,xi3,xi4）。物质浓度类别Y∈{1,2,…,J}与其特征值（颜色读数）之间存在非线性概率关系。设样本Xi的浓度属于第J类的概率为PJ，以Y=J作为参考类别，则对于Y=J（j=1,2,…,J-1），其logistic变换logit模型[5-6]为：

其中：Bj0,Bj1,…,Bj4为logistic回归的偏回归系数，表示变量xi对Y的影响大小，B0j为常数项；为样本的第j个参数值；而对于参考类别, 其模型中的所有系数均为0，即GJ=0。由式（1）得：

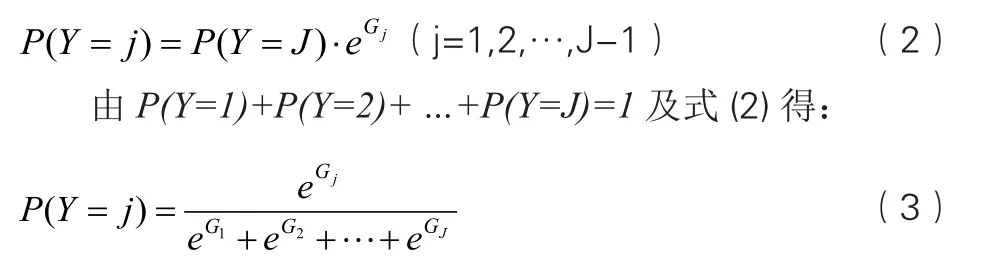
式（1）中的模型系数Bj0,Bj1,…,Bj4，由建模样本数据及统计软件SPSS19[7-8]完成。

2 数据来源及模型建立

2017年全国大学生数学建模C题给出一组二氧化硫的浓度与其颜色的读数，见表1所示。

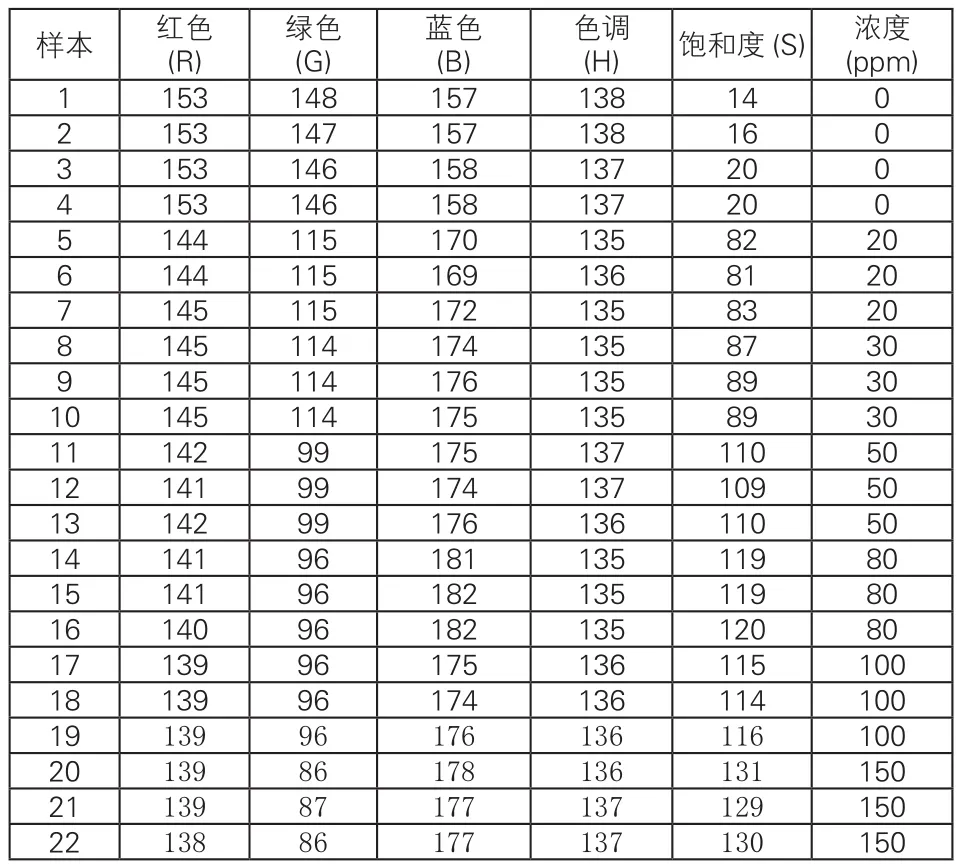
表1 二氧化硫的浓度与颜色读数

首先按浓度大小分类，将浓度为0，20，30，50，80，100，150对应的样本分别看成一类，共7类，类别值分别为1，2，3，4，5，6，7。当类别值为1时，则对应的浓度为0；当类别值为2时，则对应的浓度为20；当类别值3时，则对应的浓度为30；当类别值4时，则对应的浓度为50；依次类推。

将表1中二氧化硫指标数据及相应类别值列导入SPSS19中，选择“分析”｜“回归”｜“多项logistic”命令，按提示对话框完成所有操作，求得到的模型系数及模型见下式（4）～（10）：

由SPSS19得出模型拟合信息见表2，伪R方值见表3，拟合优度见表4。

表2 模型拟合信息

表3 三个伪决定系数R方

表4 拟合优度

从表2、表3及表4可知模型整体的显著性非常高，因为p值远小于0.05；从表3及表4可看出三个伪决定系数及拟合优度都很高，说明模型拟合效果非常好。下面给出模型的反向检验结果。

表5 归类概率及判断结果（精确到万分位）

利用式（4）～（10）及式（3）可求出样本隶属各类的概率，并按最大概率原则归类，计算结果见表5。

说明:从表5的判定结果知该模型的拟合预测精确为100%，表明logistic回归为概率型非线性回归模型具有很高的区分度，也说明将此类问题转化成类别识别或模式识别问题来解决完全可行。另外，将该类问题看成决策问题用概率统计理论方法解答克服了传统单一模型方法精确不高的缺点。

下面给同3个测试样本（2017年全国大学生数学建模C题），见表6。

表6 测试样本的二氧化硫的浓度与颜色读数

将表6中3个样本的特征指标值代入式（4）至式（10），并按式（3）求得样本属于各类的概率，并按最大概率归类，如表7所示。

表7 测试样本的浓度预测结果（精确到万分位）

可见预测精度为100%，说明多项logistic概率回归模型具有非常高的拟合预测能力，用物质浓度预测、以及其他模式识别或类别辨识完全可行。

3 结语

logistic回归模型是一种基于概率的多元非线性问题的处理方法。实例分析表明该方法用于类别辨识或模式识别具有很高的精确度。对样本物质浓度进行适当类别划分，用表征浓度的特征数值创建多项 logistic回归模型，并用统计软件SPSS估算模型系数，通过对建模样本和测试样本的拟合预测精度的分析，准确度均达到100%，表明该模型预测效果很好，值得工程技术人员借鉴。