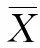基于均值控制图的设备预防维修预警决策模型研究*
2018-12-05赵永强
赵永强
(西安邮电大学 现代邮政学院,西安 710061)
0 引言
从文献综述看,很多学者在研究预防维修和控制图的集成模型时,对设备的预防维修均考虑在过程失控后进行维修,此时的设备已经出现较严重的问题,会使维修难度增加,也会导致生产出的产品质量水平下降。因此,需要考虑在控制图中设定警戒区域,当控制图点落入此区域时,就对设备进行预防维修,这样就能够保证设备依然处于正常状态时就进行预防维修,进而保证生产的有效性和可靠性。基于此,本文将控制图与设备维修决策相结合,在控制图报警时就考虑执行设备预防维修,对降低生产成本、提高设备的可靠性及产品质量有重要的现实意义。
1 模型构建的理论基础
2 模型构建
2.1 模型的研究假设
研究的基本假设如下:
(1)控制图所监测到的异常为单一系统因素造成的平均值偏移;
(2)产品的质量特性服从正态分布N(μ,σ2);
(3)过程开始时是处于受控状态,当系统因素发生后,过程的平均值由μ偏移至μ±δσ,且上下偏移的概率相等;
(4)生产过程发生异常的时间服从指数分布,其失效率参数为λ0;
(5)生产过程执行预防维修动作后,失效率可由λ0改善为λ,λ=r×λ0,0 (7)当抽样结果样本落在警戒区域(-k,-w)∪(k,w)时,则执行预防维修动作。 (8)由于预防维修无法将生产过程由异常状态恢复到受控状态,因此假设预防维修的成本小于生产过程异常后修复的成本。 (9)假设生产过程为连续性生产,即控制图监测到系统因素并开始寻找与修复生产过程时,生产不停止。 2.2.1 控制图的控制周期时间分析 (1)生产过程在受控状态的时间 假设Pw为生产过程在受控状态,抽样结果在警戒界限(-w,w)之内的概率,Φ(x)为正态分布的累计概率分布函数,w为警戒界限系数则,则Pw为: Pw=Φ(w)-Φ(-w) (1) 假设Pr为生产过程处于受控状态且抽样结果在警戒界限与控制界限之间(-k,-w)∪(k,w)的概率,即生产过程需进行预防维修活动的概率,k为控制图界限系数,则有: Pr=2[Φ(k)-Φ(w)] (2) 令h0为受控状态下每次抽样的期望间隔时间,即抽样时间间隔与预防维修时间的期望值之和;h为抽样时间间隔;Z为预防维修执行时间,则: h0=h×Pw+(h+Z)×Pr (3) 由于生产过程发生异常的概率服从指数分布,因此生产过程在受控状态下的发生概率,即尚未发生异常的概率将随时间而递减,由上述每次抽样的期望间隔时间来看,其每次抽样间隔过后生产过程的存活率分别为e-λh0,e-2λh0,e-3λh0,……,因此生产过程在受控状态到异常发生后首次抽样以前所经过的时间为受控状态的每次抽样间隔期望时间与每次抽样间隔过后生产过程的发生概率的乘积总和。令λ为系统在执行预防维修后的指数分布的失效率,即: t0=h0e-λh0+h0e-2λh0+h0e-3λh0+... (4) 令τ为异常发生前最后一次抽样到异常发生的时间,假设异常发生在第j次抽样之后,则: (5) 因此,控制内的时间T1为: T1=(h0e-λh0+h0e-2λh0+h0e-3λh0+...)-(h0-τ) (6) (2)异常发生后至控制图监测出异常的时间 (7) (8) 令h1为当异常发生后每次抽样的期望间隔时间,即抽样时间间隔与预防维修时间的期望值之和,则: (9) (10) (11) 因此,异常发生后至控制图监测出异常的时间为T2: (12) (3)抽样、检验并解释其结果的时间 令抽样、检验并解释其结果的时间为T3;e为单位产品的抽样与检验时间;n为抽样样本大小,则有: T3=e×n (13) (4)令D为异常发生后过程的修复时间,寻找异常来源及修复过程的时间T4为: T4=D (14) 由上述4个时间函数相加即可求得过程的总周期时间,即控制图的总周期时间模式为: E(T)=T1+T2+T3+T4 (15) 2.2.2 控制图的成本模式分析 在本研究的连续性生产的假设模式中,生产过程每周期的成本可分为抽样成本、假警报成本、寻找异常因素与修复生产过程的成本、预防维修成本、社会损失成本等5个部分,分别说明如下: (1)抽样成本 假设每次抽样的固定成本为a,单位成本为b,则生产过程每单次抽样的成本为a+b×n。生产过程在控制内的总时间为T1,而h0为控制内的每次抽样之间的期望间隔时间,则控制内的抽样次数为T1/h0。同理,生产过程从异常状态直到开始修复前的时间为T2+T3,每次抽样间的期望间隔时间为h1,因此控制外的抽样次数为(T2+T3)/h1。而抽样总次数为T1/h0+(T2+T3)/h1。因此抽样的总成本为C1: (16) (2)假警报成本 α为第一类错误的发生概率,即过程在受控状态时抽样结果样本在控制界限外的概率,则α=2Φ(-k),假警报的期望发生次数NOF为假警报的概率乘以控制内的抽样次数,Y为每次假警报的成本,即: NOF=α×(T1/h0) (17) 则假警报的额外成本C2为 : C2=Y×NOF (18) (3)寻找与修复异常成本 令V为异常发生后寻找异常来源与修复过程的成本,则寻找异常来源及修复生产过程的成本C3=V。 (4)预防维修成本 受控状态内执行预防维修的次数为Pr×(T1/h0),异常状态下执行预防维修的次数为Pr×ARL1,因此受控状态与异常状态的预防维修总次数为Pr×(T1/h0)+Pr×ARL1。Cpm为每次执行预防维修的成本,则预防维修的总成本C4为: C4=Cpm×[Pr×(T1/h0)+Pr×ARL1] (19) (5)社会损失成本 社会损失成本分为两部分,分别为受控状态的社会损失成本与异常状态的社会损失成本。 当生产过程在受控状态时,若M为异常状态单位时间的损失,dv为生产过程平均值与目标值间差距,Δ为产品的规格公差,T1为生产过程在受控状态的时间,u为生产过程单位时间产量,则此时的产品出厂所造成的社会损失成本为: (20) 当生产过程处于异常状态时,其平均值偏移了δσ,T2、T3、T4均为生产过程在异常状态的时间,则此时的产品出厂所造成的社会损失成本为: (21) 2.2.3 控制图的单位时间成本 上述6个成本函数相加,即可求得生产过程每周期的总成本模式,即控制图的总周期成本为: E(C)=C1+C2+C3+C4+C5+C6 (22) 故控制图的单位时间成本为: (23) 本研究利用Matlab软件求出最低损失成本及最优设计参数,算法的设计步骤说明如下: (1)找出可能的抽样样本大小n作为起始值,并以加减数个单位的n作为其搜寻范围; (2)以搜寻、比较、取代的方法找出在此范围内所有n的个别最优单位时间成本及与其对应的h、k; (3)将此范围内所有n的个别最优单位时间成本作比较、取代,以找出最优单位时间成本值; (4)若此最优单位时间成本值的n不位于搜寻范围的端点时,则此时的n、h、k值即为本研究的最优n*、h*、k*。 现假设所有参数数据分别为:λ0=0.05、r=0.8、Z=0.1、e=0.2、D=1、a=2、b=0.5、Y=500、M=900、V=1100、Cpm=200、δ=0.5、σ=2、Δ=8、dv=1、u=100。将上述参数代入本研究的模型中,初步运行结果如表1所示。 表1 n、h、k与 E(TC)的运行结果 在表1中,当抽样样本数n为14时,其单位时间成本E(TC)的值为3281.70,为最低。此时n*=14、h*=0.594、k*=1.899,为最优的控制图设计参数。在n*=14、h*=0.594、k*=1.899三个参数值不变的条件下,令r=1、Z=1、Cpm=0,此时的控制图模型不考虑设备预防维修,通过计算得出E(TC)的值为3523.44,比考虑预防维修的数值增加,说明在警戒区执行预防维修的控制图经济性模型相对于不考虑预防维修的模型更为经济。通过数据比对可知,结合控制图经济性模型设备维修预警决策模型是可行的,经济性最好且设备的可靠性更好,这对提高产品质量、降低质量成本及提高设备可靠性十分有利。 为探讨各参数资料对于n、h、k以及E(TC)的影响程度,将各项参数资料δ、M、λ0、Y、r,Δ、Z,dv、e、Cpm、Z、r分别导入。整个模型分为5个等级进行敏感性分析,其结果如表2所示。 表2 参数的敏感性分析 具体参数分析如下: (1)当M值增加时,将使单位时间成本E(TC)增加,抽样间隔h增加,控制图界限宽度减少; (2)当δ值增加时将使单位时间成本E(TC)增加,抽样间隔h增加,控制图界限宽度k减少; (3)当λ0值增加时将使单位时间成本E(TC)增加,样本数n减少,抽样间隔h增加,控制图界限宽度k减少; (4)当e值增加时将使单位时间成本E(TC)增加,样本数n减少,抽样间隔h增加,控制图界限宽度k减少; (5)当Y值增加时将使单位时间成本E(TC)增加,抽样间隔h增加,控制图界限宽度k减少; (6)当Δ值增加时将使单位时间成本E(TC)减少,样本数n增加,抽样间隔h增加Δ控制图界限宽度k增加; (7)当dv值增加时将使单位时间成本E(TC)增加,样本数n增加,抽样间隔h减少控制图界限宽度k减少; (8)当Cpm值增加时将使单位时间成本E(TC)增加,抽样间隔h增加,控制图界限宽度k减少; (9)当r值增加时将使单位时间成本E(TC)增加,抽样间隔h增加,控制图界限宽度k减少。
2.2 模型的构建




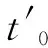
2.3 参数分析
3 算例分析


4 结论