加工中心用永磁同步电主轴动态特性分析*
2018-12-05于慎波王程程
于慎波,王程程
(沈阳工业大学 机械工程学院,沈阳 110870)
0 引言
在当代高速制造加工技术不断发展的今天,较高的进给、切削速度以及高加工精度成为了制造业二次革命性飞跃的重要因素,高速加工技术已经成为世界各国竞相发展的趋势。电主轴作为现代高速加工中心的主要主轴形式,其具有使用寿命较长、回转精度较高、振动和噪音小、摩擦功耗小等等特点,由于其具有较好的稳定性和较高的动态精度,使得高速加工更容易实现[1-4]。
在实际工作当中,作为高速加工中心的核心部件之一,电主轴的旋转速度达到某一特定值时,会出现强烈的振动,转子本身固有频率和其强迫振动频率向吻合,引起共振[5]。共振进而引起转子振动过载,同时与轴承之间的相互作用力增大,横向振动位移也逐渐增大,使得系统整体的稳定性不能得以保证,大大降低了电主轴的使用寿命。因此电主轴临界转速计算和稳定性分析显得尤为重要。
使用有限元法计算转子临界转速时,实际上就是将指定模型简化成为若干单元后,通过特定因素将其联结组合。此算法将建模过程简化,不需要列出转子运动方程式,借助于计算机能够进行复杂大型模型计算,具有较快的计算速度[6-7]。传递矩阵法经过几十年的完善和发展具有显著的特征,当模型自由度增加时矩阵维数保持不变,编程求解过程简单,计算量大大减小进而节省计算时间,但是在进行复杂结构大型转子模型计算时,会出现根的值上下溢出的现象[8-9]。
本文使用加时间因子的传递矩阵计算方法,能够有效的解决前人方法中根的值上下溢出的问题,同时大大提高了计算精度。在进行不平衡响应分析时,绘制三维图形,能够更加直观的反应电主轴工作时的响应情况,并且结合对数衰减率曲线,使得判断稳定性裕度的结果更加准确。
1 电主轴临界转速计算
1.1 转子离散化
进行解析计算的第一步是要将转子进行离散化处理,实际上就是把整个轴看成是由无质量的变截面弹性轴段和刚性的质量圆盘组合而成。图1为本文所研究的电主轴简图,节点的选取在轴截面突变处以及质心处,本实例中,将转子划分为18个轴段,19个节点,同时在质量点附加相应的质量以及转动惯量,其他节点省略,图中标出4、7、14、16点为轴承支撑点。
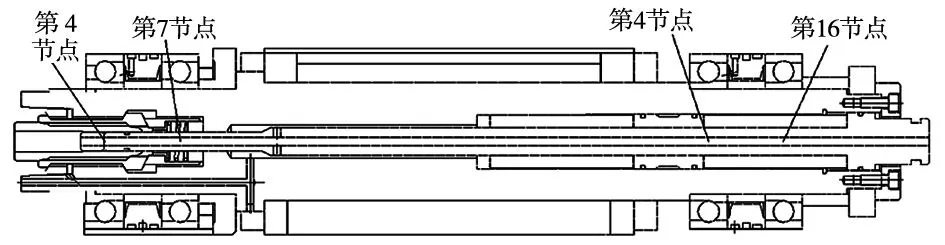
图1 XDJ30—00电主轴转子及支承简图
在进行转子离散化处理时主要遵循的原则是集中质量原则,实际上就是将轴系的整体质量集中分散到各个轴段上,此法的核心原则就是要保证轴系的质心位置不变,同时简化之后的总质量与简化之前的总质量相等,两种模型的状态相同。在进行转动惯量集中时,遵循转动惯量不变的原则,每设置一个节点则节点两端的轴段轴截面相同[10-11]。
1.2 转子的传递矩阵
对于转子的第i个部件,将其左右两端截面的编号分别记为i和i+1,则利用每一截面的径向位移、转角、弯矩和剪力所组成的阵列,称为该截面的状态向量,用式(1)来表示:
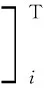
(1)
式中,Mx、My,Qx、Qy,x、y,θx、θy分别为两个方向的弯矩、剪力、挠度和转角。
任一部件两端截面的状态向量之间存在一定的关系,见式(2):
{Z}i+1={T}i{Z}i
(2)
式中,{T}i为该部件的传递矩阵,{T}i={B}i{D}i,其中{B}i为无质量等截面弾性轴的传递矩阵,{D}i为刚性薄圆盘的传递矩阵,为使得计算更加方便精确,引入振动量用复数来表示,见式(3):
S=λ+iω
(3)
式中,S为复涡动频率,由实部和虚部组成,实部λ表示衰减指数,虚部ω表示阻尼圆周率。
在本文计算过程当中,提出加时间因子的算法,使用VB编程计算得出复频率实部和虚部,计算时除转速除以时间因子之外,其他计算参量和时间因子相乘,这一过程能够平衡计算中小数和大数之间的差异,进而进行传递矩阵的运算。传递矩阵运算输出数值为复频率,计算结束后将复频率和时间因子相乘得出临界转速值,输出数据上下溢出的问题得以解决。
1.3 解析法计算XDJ30—00电主轴临界转速
本文以额定功率为22kW的永磁同步电主轴为例,用传递矩阵法计算此电主轴的临界转速,画出坎贝尔图见图2。时间因子取值8000,以2500r/min为转速序列公差。从图中我们能够看到,当电主轴自转频率逐渐增大时,一阶正反向涡动频率变化不大且相似,二阶反向涡动频率逐渐减小而二阶正向涡动频率逐渐增大,图中同频线与各阶涡动频率曲线的交点值为临界转速。
1.4 有限元法计算电主轴临界转速
有限元方法计算首先应当建立二维质量点模型,MASS用来模拟质量点单元,BEAM为无质量弾性轴单元,同时在轴承支撑点模拟弹簧阻尼单元,完成上述建模之后,在不同节点处根据其运动方式施加不同方向的约束,轴承为支撑固定装置,施加全约束,其他质量点主要施加旋转约束,施加完约束后的二维轴系模型如图3所示。

图3 ANSYS二维质量点单元模型
以2000r/min为转速序列公差,进入通用后处理器(General Postprocessor),绘制出转子系统的CAMPBELL图见图4。当自转频率增高时,一阶正向涡动(FW)频率和反向涡动(BW)频率相似,在图中基本重合;二阶反向涡动频率减小,二阶正向涡动频率增大,从图中提取同频线与各阶涡动频率的交点,由于不平衡激励力的存在,使得转子在工作时将做同步正进动,因此通常情况正涡动频率和同频线交点为临界转速。

图4 有限元法计算电主轴临界转速坎贝尔图
1.5 解析计算与ANSYS计算结果对照
由表1中可知ANSYS有限元计算结果与传递矩阵法的计算结果基本一致,验证加时间因子t的传递矩阵法的正确性。

表1 临界转速计算结果对比(r/min)
2 不平衡响应分析
转子的不平衡响应主要目的是分析转子对于某些不平衡量的敏感程度,不平衡响应分析能够为转子结构参数的设计提供依据。与求临界转速类似,本文使用传递矩阵的方法,首先要建立盘轴单元的力学模型,列出圆盘运动微分方程[12-14]。将此电主轴划分为20个质量点,且不平衡磁拉力作用位置为第13点。设转子自转角速度ω。圆盘运动微分方程建立选取OXYZ坐标系,圆心坐标为x,y,质心坐标为xc,yc,动坐标系为o′ξη,型心坐标如下:
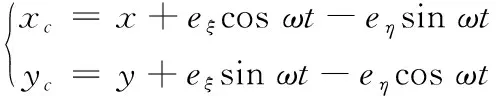
(4)
U为不平衡质量矩,U=me,得:

(5)
θx、Mx、Qx,θy、My、Qy分别为xoz和yoz平面内的转角、剪力和弯矩,则运动微分方程,见式(6):
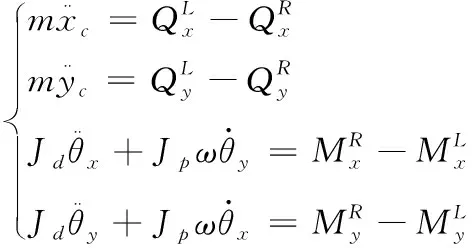
(6)
代入质心的动量定理,得:
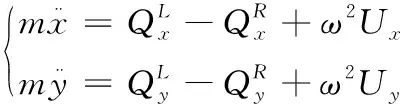
(7)
同样是利用传递矩阵的方法,首先列出传递矩阵和频率方程式,根据设定的初始条件逐段递推求得复位移量进而求出各个截面的状态向量。传递矩阵简化后见式(8):
(8)
(9)

即求得各节点的振幅和相位。当旋转机械的转速较高时,很小的偏心也会产生很大的离心力,此离心力会导致轴系出现振动。当偏心为零时,转子的不平衡响应如图5a所示,设转子存在0.1mm动态偏心,进而产生偏心力为88.2N时转子的不平衡响应如图5b所示。从图中可得,当电主轴旋转速度到达临界转速附近时,各个节点的振动幅度逐渐增大。与此同时不平衡磁拉力使得转子一阶振幅明显增大。
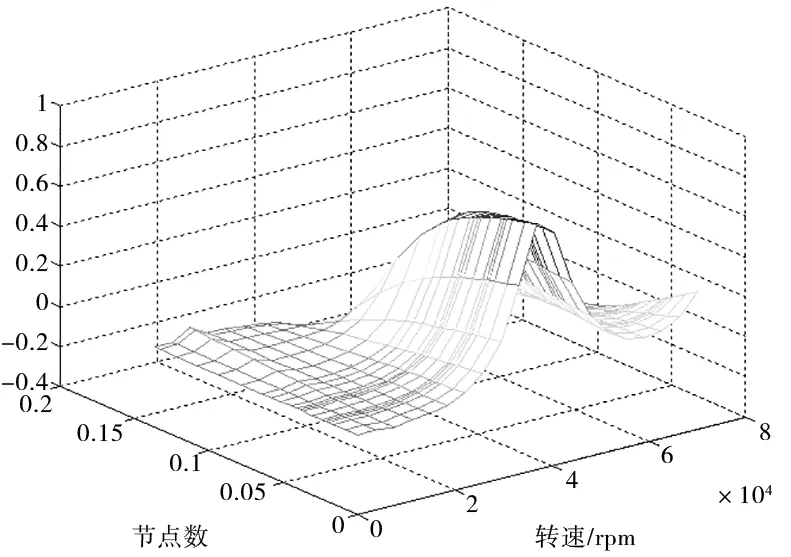
(a) 偏心为0

(b)偏心0.1mm图5 不平衡响应随转速变化关系
图6分别为转速10000r/min、25000r/min时转子轴承系统的不平衡响应情况。当旋转速度在临界转速附近时转轴旋转振动位移较大,稳定性较低。

(a)转速10000r/min (b)转速25000r/min图6 转速不同时电主轴响应情况
3 永磁同步电主轴稳定性分析
对数衰减率主要反映的是振幅衰减的速率,能够有效的对系统的稳定性裕度进行分析。稳定性裕度体现在系统自身的修复能力,也就是能够回到平稳状态的能力[15]。对数衰减率是对这一系列过程的度量并且能够直观表示出轴系的稳定性裕度。针对此转子系统,运用Matlab画出其对数衰减率曲线,分析轴系的稳定性裕度。
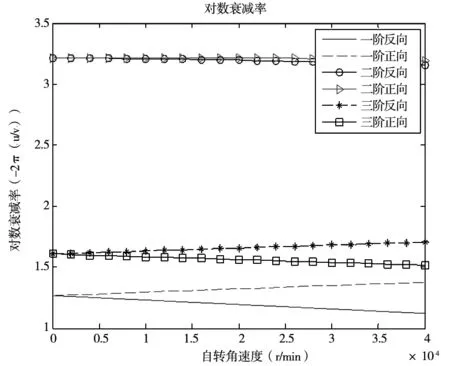
图7 电主轴对数衰减率曲线
分析此转子的对数衰减率曲线,其中一阶涡动的衰减率下降最快,其表征了较小的稳定性裕度,易导致轴系失稳,是预防失稳需要特别关注的方面。
4 结论
(1)运用增加时间因子的传递矩阵法计算永磁同步电主轴各项异性支承的有阻尼转子-轴承系统的临界转速。用双重步QR法计算频率方程,有效地解决了上下溢出和丢根的问题。
(2)分析了高速永磁同步电主轴考虑不平衡磁拉力的响应随转速的变化规律。当转速到达临界转速附近时,振幅逐渐增大。同时得到了轴系临界转速随转速变化的分布情况。
(3)分析了永磁同步电主轴转子的对数衰减率曲线,其中一阶反向涡动的对数衰减率下降趋势明显,其表征了较小的稳定性裕度,易导致轴系失稳。
