基于Gauss指数摩擦模型的3-RPS并联机构动力学建模*
2018-12-05张彦斐宫金良王志文
金 鹏,张彦斐,宫金良,王志文
(山东理工大学 机械工程学院,山东 淄博 255049)
0 引言
并联机构具有结构紧凑、定位精度高等优点,在并联机床等领域得到广泛应用[1-3]。为实现对并联机构的动态控制,需要建立机构的动力学模型[4-6]。目前,并联机构的动力学建模方法主要有拉格朗日方程法[7]、牛顿-欧拉法[8]和凯恩方程法[9]等。为便于数学建模,研究人员一般忽略关节摩擦或仅考虑驱动副摩擦[10]对机构动力学模型的影响,使得所建动力学模型与实际相差较大。
在考虑关节摩擦的动力学建模过程中,摩擦模型的选择至关重要[11]。相比静态摩擦模型,动态摩擦模型能够较好的描述铰接构件在预滑动阶段的摩擦行为,但该类模型所需辨识的参数太多,且某些参数的辨识较为困难,当辨识精度无法满足时,选择动态摩擦模型的优势并不明显。静态摩擦模型中,以库伦摩擦模型、“库伦+黏性”摩擦模型和指数摩擦模型应用最多,前两种摩擦模型将关节摩擦描述为速度的线性函数,但在低速运动阶段,随关节速度的增大,关节摩擦具有非线性变化的特点,与实际摩擦力相比,基于前两种摩擦模型所求得的关节摩擦误差较大。指数摩擦模型通过引入负斜率指数项,更加符合低速运动时关节摩擦的真实情况[12]。因此,本文基于Gauss指数模型对各运动副的关节摩擦进行定量描述。
为定量分析关节摩擦对机构驱动力的影响,基于运动学模型和拉格朗日方程建立机构理想动力学模型。基于Gauss指数模型和修正后的拉格朗日算子建立考虑全部关节摩擦的动力学模型。在同一运动规律下,通过与ADAMS仿真结果进行对比,验证了模型的正确性和摩擦补偿的必要性。
1 运动学分析
1.1 结构描述
3-RPS并联机构由动平台、定平台和三条驱动支链组成,如图1所示。
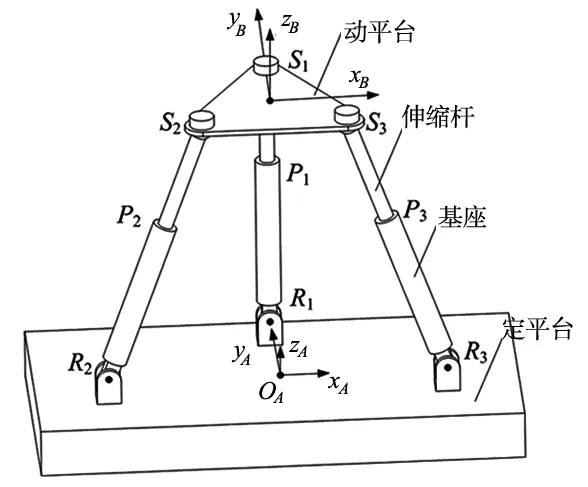
图1 3-RPS并联机构
驱动支链的伸缩杆和基座构成移动副P,伸缩杆和动平台通过球铰副S连接,基座和定平台通过转动副R连接。球铰副转动中心S1、S2和S3构成等边三角形,转动副R1、R2和R3构成等腰三角形(R1R2=R1R3,∠R2R1R3=120°)。等边三角形S1S2S3的边长为k, 等腰三角形R1R2R3的底边R2R3长为3k。以R2R3的中点OA为原点建立固定坐标系OAxAyAzA,以等边三角形S1S2S3的几何中心点OB为原点建立运动坐标系OBxByBzB。各转动副的转动轴均与定坐标轴OAyA平行。由于三条驱动支链的约束作用,动平台可实现沿坐标轴OAxA和OAzA的平移,以及绕坐标轴OByB的转动。
1.2 逆运动学模型
以操作空间动平台的位姿矢量[xB,zB,θ]T为机构的广义坐标,其中xB和zB为动平台几何中心点OB在坐标系OAxAyAzA中的坐标值,θ为坐标轴OBzB和坐标轴OAxA的夹角。根据图1可知,在矢量三角形OAOBS3和矢量三角形OAR3S3中,
OAS3=OAOB+OBS3
(1)
R3S3=R3OA+OAS3
(2)
式(1)中,
则,
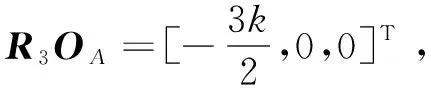
(3)
与上同理,基于矢量三角形OAOBS1和矢量三角形OAR1S1可得:
R1S1=[xB,0,zB]T
(4)
基于矢量三角形OAOBS2和矢量三角形OAR2S2可得:
(5)
设移动副Pn输入位移为Δqn(n=1,2,3),由式(3)~式(5)建立逆运动学模型。
(6)
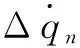
其中,J为机构速度雅可比矩阵。
2 关节约束力
为建立包含全部运动副摩擦的动力学模型,需对关节约束力进行定量分析。在受力分析过程中,对于同一力矢量,其具体表示方法和坐标系的选择有关。已知局部坐标系绕坐标轴OAyA逆时针转动α,设该力矢量在定坐标系中可表示为F1,在局部坐标系中可表示为F2,则F1和F2存在如下关系:
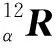
2.1 驱动支链受力
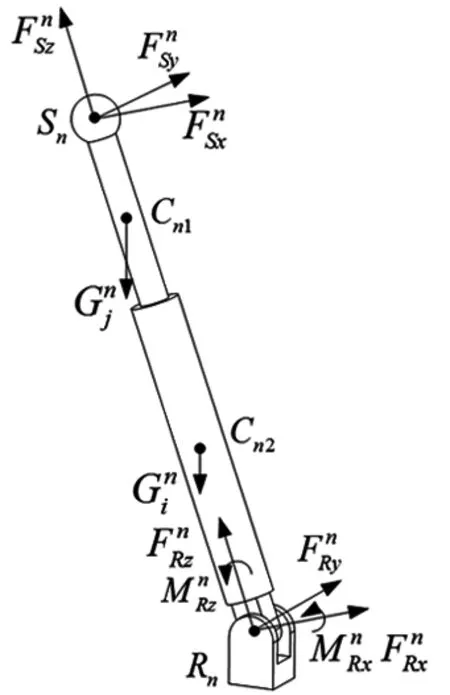
图2 驱动支链受力

由达朗贝尔原理可建立力平衡方程:
(7)

其中,aj=[0,0,ajz]T为伸缩杆在局部坐标系中的加速度。对转动副Rn的局部坐标轴取矩可得:
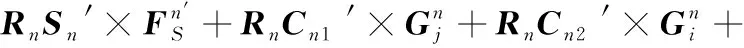
(8)
式(8)中,
RnSn′=[|RnSn|·cosφn,0,|RnSn|·sinφn]T
RnCn1′=[|RnCn1|·cosφn,0,|RnCn1|·sinφn]T
RnCn2′=[|RnCn2|·cosφn,0,|RnCn2|·sinφn]T

其中,
Ii和Ij为基座和伸缩杆绕质心坐标轴的转动惯量。
2.2 伸缩杆受力

图3 伸缩杆受力
与2.1节同理,伸缩杆的力平衡方程为:
(9)
对移动副Pn的局部坐标轴取矩,伸缩杆的力矩平衡方程可表示为:
(10)
其中,
PnSn′=[|PnSn|·cosφn,0,|PnSn|·sinφn]T
PnCn1′=[|PnCn1|·cosφn,0,|PnCn1|·sinφn]T
2.3 动平台受力
当动平台所受工作负载为FOB和MOB时,其受力如图4所示。
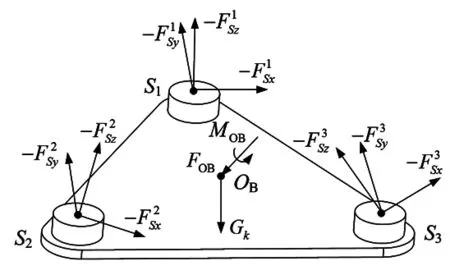
图4 动平台受力
对于动平台,其力平衡方程为:
(11)
式中,Gk为动平台的重力,FIk′为动平台在定坐标系中的惯性力。
Gk=[0,0,-mkg]T,FIk′= -mk·ak

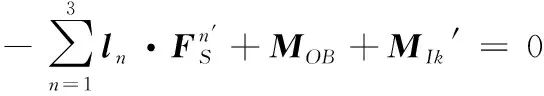
(12)
式中,
MIk′为动平台绕定坐标轴的惯性力矩。
式中,
其中,Ik为动平台绕质心坐标轴的转动惯量。式(7)~式(12)共有42个平衡方程,对应有42个独立变量,通过联立式(7)~式(12)即可求得全部关节约束力。
3 动力学建模
在建模过程中,忽略构件的柔性变形和运动副间隙对动力学模型的影响,并选择平面xAOAyA为机构的零势能面。
3.1 动平台
动平台的动能为:
(13)
式中,Iky′为动平台绕坐标轴OAyA的转动惯量。动平台的势能为:
Uk=mkg·zB
(14)
3.2 驱动支链
为求得伸缩杆质心Cn1和基座质心Cn2的坐标值,建立矢量三角形OASnCn1和矢量三角形OARnCn2,如图5所示。
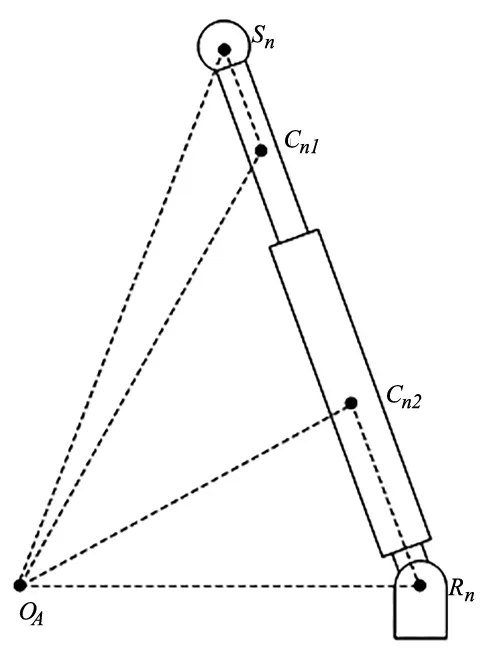
图5 伸缩杆和基座质心
在矢量三角形OASnCn1中,
OACn1=OASn+SnCn1
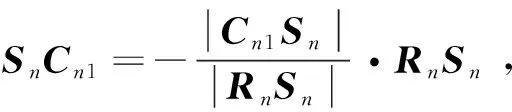
OACn1=[XCn1,YCn1,ZCn1]T
同理,在矢量三角形OARnCn2中,
OACn2=OARn+RnCn2
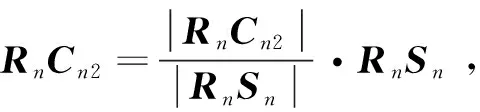
OACn2=[XCn2,YCn2,ZCn2]T
在机构运动过程中,驱动支链的动能为:

(15)
其中,Iiy′和Ijy′为基座和伸缩杆绕坐标轴OAyA的转动惯量。驱动支链的势能为:
(16)
3.3 运动副摩擦
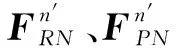
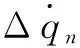
TRn=[fRc+(fs-fRc)e-(vRn/vs)2]·sgn(vRn)+fvvRn
(17)
式中,fs为最大静摩擦力,vs为Stribeck速度,sgn()为符号函数,fv为黏性摩擦系数。同理,移动副的摩擦力可表示为:
(18)
球铰副的摩擦力矩为:
TSn=[fSc+(fs-fSc)e-(vSn/vs)2]·sgn(vSn)+fvvSn
(19)
若移动副的输入位移为Δqn,基于运动学分析可得转动副和球铰副的角位移为ΔφRn和ΔφSn。机构运动过程中,关节摩擦所做的功可表示为:
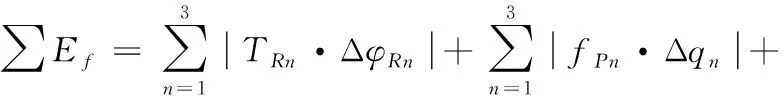
(20)
3.4 逆动力学模型
若不考虑运动副摩擦,由式(13)~式(16)可建立理想情况下的逆动力学模型为:
(21)
式中,L=Ek+Ei+j-Uk-Ui+j。若考虑运动副摩擦,
由式(13)~式(16)和式(20),可建立包含全部关节摩擦的逆动力学模型:
(22)
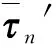
4 算例分析
机构参数如下,动平台、伸缩杆和基座的质量为3.66kg、1.96kg和4.10kg,各构件绕质心坐标系的转动惯量(kg·mm2)为Ii=diag(40435.72,40438.33,1465.90),Ij=diag(17211.20,17211.20,291.47),Ik=diag(26477.91,26477.89,52625.94)。动平台边长k=300mm,伸缩杆质心Cn1到球铰副转动中心Sn的距离为112.67mm,基座质心Cn2到转动副Rn的转动轴的距离为172.62mm。移动副的输入位移为零时,d1=558.55mm,d2=593.28mm,d3=593.28mm,φ1=90°,φ2=70.30°,φ3=109.70°。转动副轴径为25mm,球铰副的球体直径为50mm。fv=0.05,μ=0.12,vs=0.20[10],fs=9.35N。工作载荷为[150N,150N,150N,100N·m,100N·m,100N·m]T。动平台的运动轨迹为:

将装配体导入ADAMS中,在忽略摩擦和考虑摩擦两种情况下分别进行一个周期的仿真实验。基于式(21)、式(22)的各移动副驱动力理论值和基于ADAMS的仿真值如图6~图8所示。

图6 移动副1驱动力

图7 移动副2驱动力

图8 移动副3驱动力
可以看出,忽略关节摩擦时,基于式(21)的驱动力理论值和基于ADAMS的仿真值具有一致的变化趋势。考虑关节摩擦时,基于式(22)的驱动力理论值和基于ADAMS的仿真值也具有一致的变化趋势。上述两种情况中,基于式(21)和式(22)的模型误差均在3.5%以内,验证了所建动力学模型的正确性。通过对比理想动力学模型和考虑全部关节摩擦的动力学模型,移动副1、2和3的驱动力相对误差分别为11.7%、16.3%和18.5%。
在局部润滑阶段(0~0.25s),关节处两铰接构件以“固体-固体”的直接接触为主,随着关节速度的增大,关节处润滑介质逐渐均匀分布于两构件之间,构件接触变为“固体-润滑介质-固体”的间接接触,导致忽略摩擦和考虑摩擦的驱动力差值逐渐减小。在充分润滑阶段(0.25~0.75s),关节摩擦主要来源于润滑介质的粘附作用,关节速度由增大变为减小,使得忽略摩擦和考虑摩擦的驱动力差值先增大后减小。在0.75~1s,关节摩擦由充分润滑阶段变为局部润滑阶段,随着关节速度的减小,关节摩擦对驱动力的影响与0~0.25s相反。
5 结论
针对本文提出的新型3-RPS并联机构,在运动学分析的基础上,通过拉格朗日方程法建立理想动力学模型。基于Gauss指数模型,建立考虑全部运动副摩擦的动力学模型。通过对比数值算例中MATLAB的理论结果和ADAMS的仿真结果,验证了所建动力学模型的正确性。通过对比理想驱动力和考虑全部关节摩擦的驱动力,验证了摩擦补偿的必要性。
在局部润滑阶段,随着关节速度的增大,铰接构件由直接接触逐渐变为间接接触,关节摩擦具有负斜率变化的特点。在充分润滑阶段,铰接构件为间接接触,关节处润滑介质的粘附作用对关节摩擦的影响较大。分析结果为机构控制系统的摩擦补偿奠定了基础,建模方法同样适用于其他并联机构的动力学研究。
