波浪浪向角对多体浮式平台水动力性能的影响*

罗若，刘祚秋，彭泽宇

(1. 中山大学工学院应用力学与工程学系，广东 广州 510006；2. 江苏中路工程技术研究院有限公司，江苏 南京 211800)

近年，多体浮式海上平台在海工领域得到越来越广泛的应用。其通过柔性连接件将多个浮体单元加以连接，使之成为超大型海洋浮式结构物(VLFS，very large floating structure)。我国人口众多、可利用陆地空间有限，但拥有广阔的海洋资源。加快多体浮式海上平台的研究工作对于提高海洋资源的开发利用能力、维护国家海洋权益、实现海洋强国的目标具有重要意义。

早在20世纪70年代，国外就开始开展相关的研究工作。日本等国专门成立了相关的技术委员会，成功研发出浮箱式海洋平台，并对其可行性进行了试验验证[1]；美国也紧随其后提出了半潜式的海洋平台构想，并对平台性能进行了系统的研究[2]。而我国在该领域的研究相对起步稍晚，吴有生等[3]采用三维水弹性方法对超大型浮式结构物的运动和连接器响应进行了分析；大连理工大学勾莹等[4]运用边界积分法研究了波浪与两个相连浮体的相互作用问题，计算中考虑了浮体相互间的水动力干涉以及连接件约束；徐道临和张海成等[5-6]在2013年召开的“海洋结构与装备的关键基础科学问题”研讨会上做了《超大型浮动平台网络动力学稳定性研究》的报告，首次提出了利用网络动力学方法求解大型多体浮式结构的运动响应问题，这为海上多体平台研究提供了一种新的思路。多体浮式平台可以看成是一种典型的非线性动力学网络，而实际海况又是一个变化波浪频率、方向的复杂条件集合。因此，在这种条件下多体浮式平台的动力响应就变成了一个非常复杂的问题。本文针对一种链式多体浮式结构进行了讨论，并利用有限元方法对该结构在不同波浪频率和不同浪向角下的水动力响应进行了频域分析。

1 多体浮式平台模型

1.1 物理模型

本文选取的大型长链式浮式平台由若干浮块单元通过柔性连接件连接而成，如图1所示。模块M1、M2、M3、M4通过缓冲型连接件连接，相对线弹性连接而言，这种连接方式具有强抗扭能力。同时，在受压时这种连接方式能减少因弹性振荡引起的连接键内应力和位移。M1、M4端用多点系泊加以约束，以防止在波浪作用下发生结构漂移。结构受浪方向定义为波浪主轴和x轴正方向夹角。由对称性可知，本文讨论范围在0°～ 90°之间。

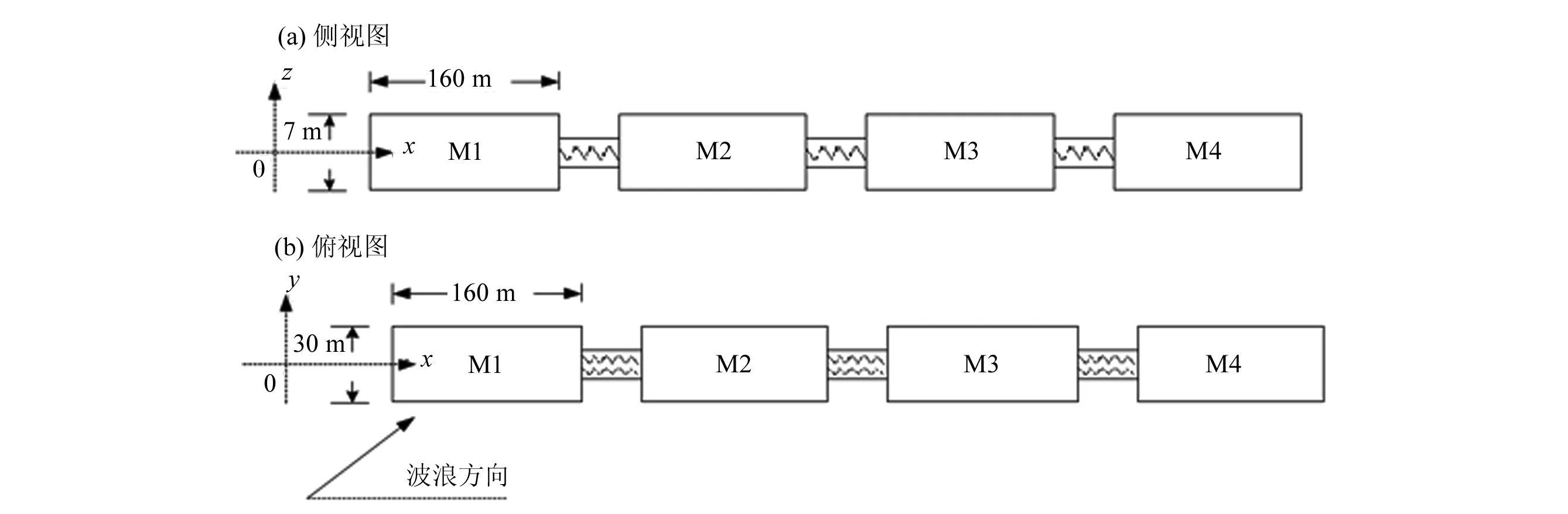
图1 浮式结构示意图Fig.1 Sketch for the floating structure

1.2 相关参数

假设浮式平台本身刚性且不透水，浮体重心处于z轴上，平台结构的具体参数为：

表1 浮块单元的参数Table 1 Parameters of floating module

海况方面，浪高取东海观测海况中的夜间大浪高3 m,水深取近海均值90 m。由于近海浪况的复杂性，波浪频率取一个低值和高值用以比较，分别为0.08和0.14 Hz。

2 理论模型

对于在波浪中运动的单个浮块，根据牛顿第二定律，其运动满足：

(1)

其中，Mi为浮式模块的质量矩阵，取决于浮块本身的质量和形状；Xi为浮体位移矩阵，在三维运动中包括三个线位移和三个角位移；Fi为浮体受到的外部力(矩)，主要包括连接件作用力、波浪作用力和平台系泊力：

Fi=Fi,k+Fi,wave+Frope

(2)

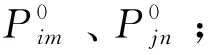
(3)

Δlim,jn=Pim-Pjn

(4)

其中，矩阵T为仿射变换矩阵。它是浮块单元形状的体现，其值可由立体几何原理求得，如下式(5)所示。式中，α、β、γ表示浮块单元的纵摇、横摇、艏摇。

(5)

对于波浪作用力Fi,wave的求解，根据势流理论，有限水深下其微幅波势函数为[6,8]：

φ(x,y,z,t)=

(6)

其中，A表示浪高，g表示重力加速度，ω表示波浪频率，K表示波数，H表示水深。作用在浮块上的波浪力主要包括三个部分：一阶力为波浪入射对接触面的动压力，即弗洛德—克里洛夫波浪力，可由伯努利方程沿浮块湿表面对势函数积分求得；二阶力为绕射力，可由拉普勒斯积分得到；三阶力为辐射作用力，体现为阻尼项。波浪力可以简化成如下表达形式：

(7)

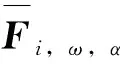
在一般作业条件下，浮式平台要求保持较好的自持性，通常采用多点系泊以约束平动和转动。本文对系泊系统采用平均刚度矩阵，故系泊力矩阵Frope表示为：

Frope=KXi

(8)

其中，K为系泊刚度矩阵，在平均刚度假设下表现为对角矩阵，其元素值本文取1×108。

3 多体浮式平台水动力性能频域/

时域分析

3.1 多体浮式平台水动力性能频域分析

在频域分析中，需要重点关注的是浮体的幅值响应算子(response amplitude operator，RAO)，它代表了结构对波浪的响应程度。通过对浮式结构湿表面进行边界元求解，我们可以得到幅值响应算子-频率的关系图。浮块M2在不同浪向角下的纵荡、横荡、垂荡的幅值响应算子，如图2所示。

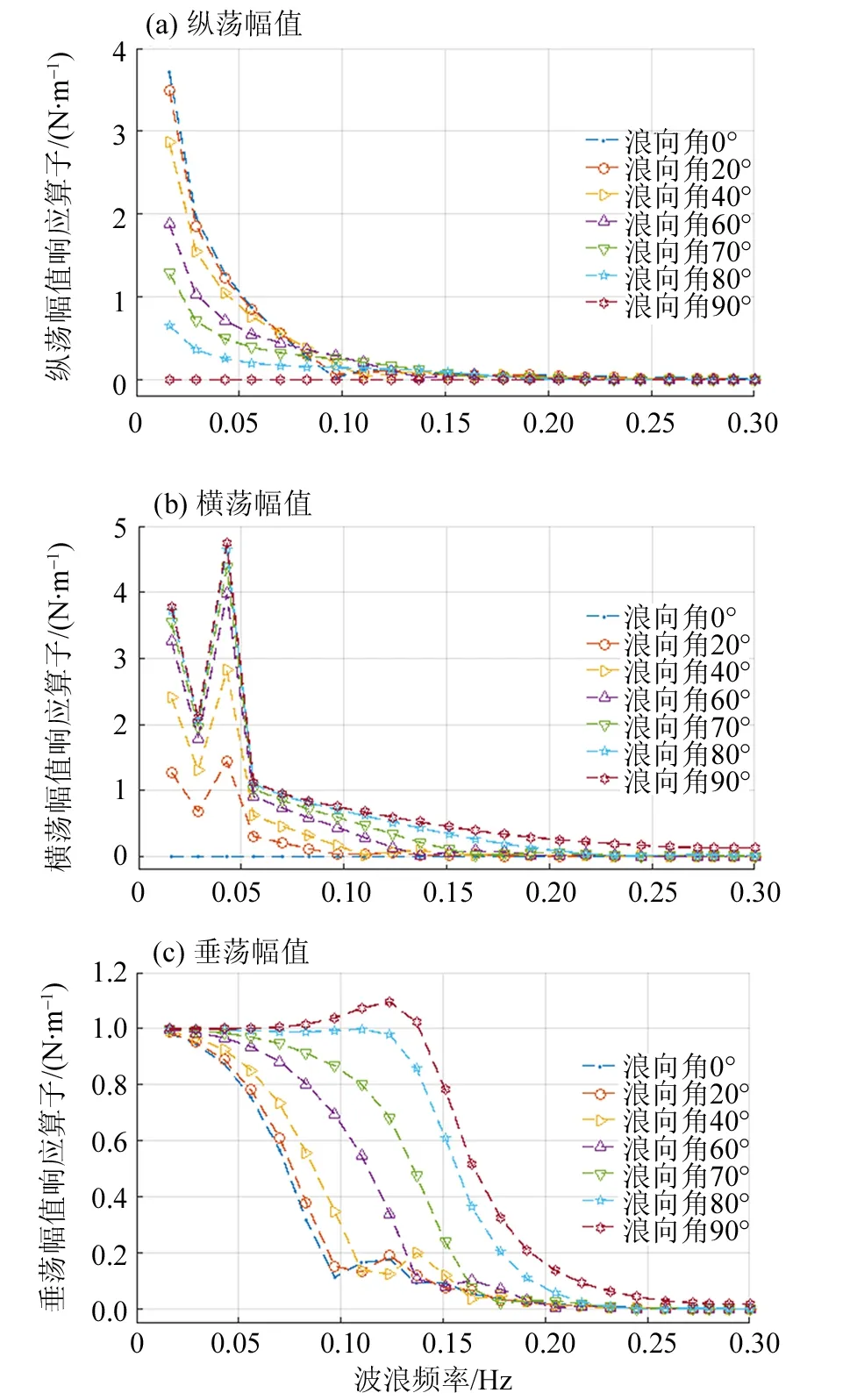
图2 不同浪向下模块M2的幅值响应算子Fig.2 RAO in different wave direction angles

从图中可以发现，纵荡幅值响应算子随着波浪角的增大而逐步减少，在频率大于1.35 Hz以后，各浪向角下的响应已接近0，可见大于此频率时结构的抗性较好；而频率小于0.068 Hz左右时幅值响应算子的增速很快，可见此时浮块的耐波性差。横荡幅值响应算子的变化在高频时与纵荡类似，响应区域也明显随着浪向角增大而增大；当浪向角达到90°时，响应区域已延伸到0.3 Hz，且在0.046 Hz附近有一个极大值，其响应系数接近5，可见横浪时在横荡方向产生的响应幅值明显大于其他自由度。垂荡幅值响应算子同样随着浪向角增大而增大；浪向角90°时，在0.137 Hz以下幅值响应算子值几乎没有变化，而此范围涵盖了近海的大部分波频，可见浮块垂荡较为稳定。

波浪力可视为一个随时间变化的参量，用波浪力算子表示其变化幅度。通过对浮块单元的湿表面进行表面元求解，可以得到波浪力算子的变化情况。图3列出了波浪力算子在不同频率、不同浪向角时的变化情况。

图3 模块M2的波浪力算子Fig.3 Wave forces on module M2

从图中可以看出：在高频和低频下，波浪力的变化表现出明显不同的趋势。在高频波浪下波浪力幅值在60°时有一个极小值，这说明绕射作用力和克里诺夫作用力的影响互相耦合；低频下波浪力幅值随浪向角的变化相对平滑，横荡、垂荡方向随浪向角的增大而持续增大，由于图示模块长宽比较大，可见低频时一阶波浪力起到主导作用。

3.2 多体浮式平台水动力性能时域分析

对于海上浮式平台的时域响应，利用四阶龙格库塔迭代方法进行求解。我们分别求出了不同入射角度和高、低频下浮块M2的响应幅值，迭代步长取0.1 s。由于浮块通过弱非线性连接键连接，不同自由度间显然存在互相影响，因而其运动在很多情况下将呈现强非线性。

图四展示了在一个较高频率的波浪下的模块M2的位移响应幅值和结构中模块间连接刚度的变化关系。

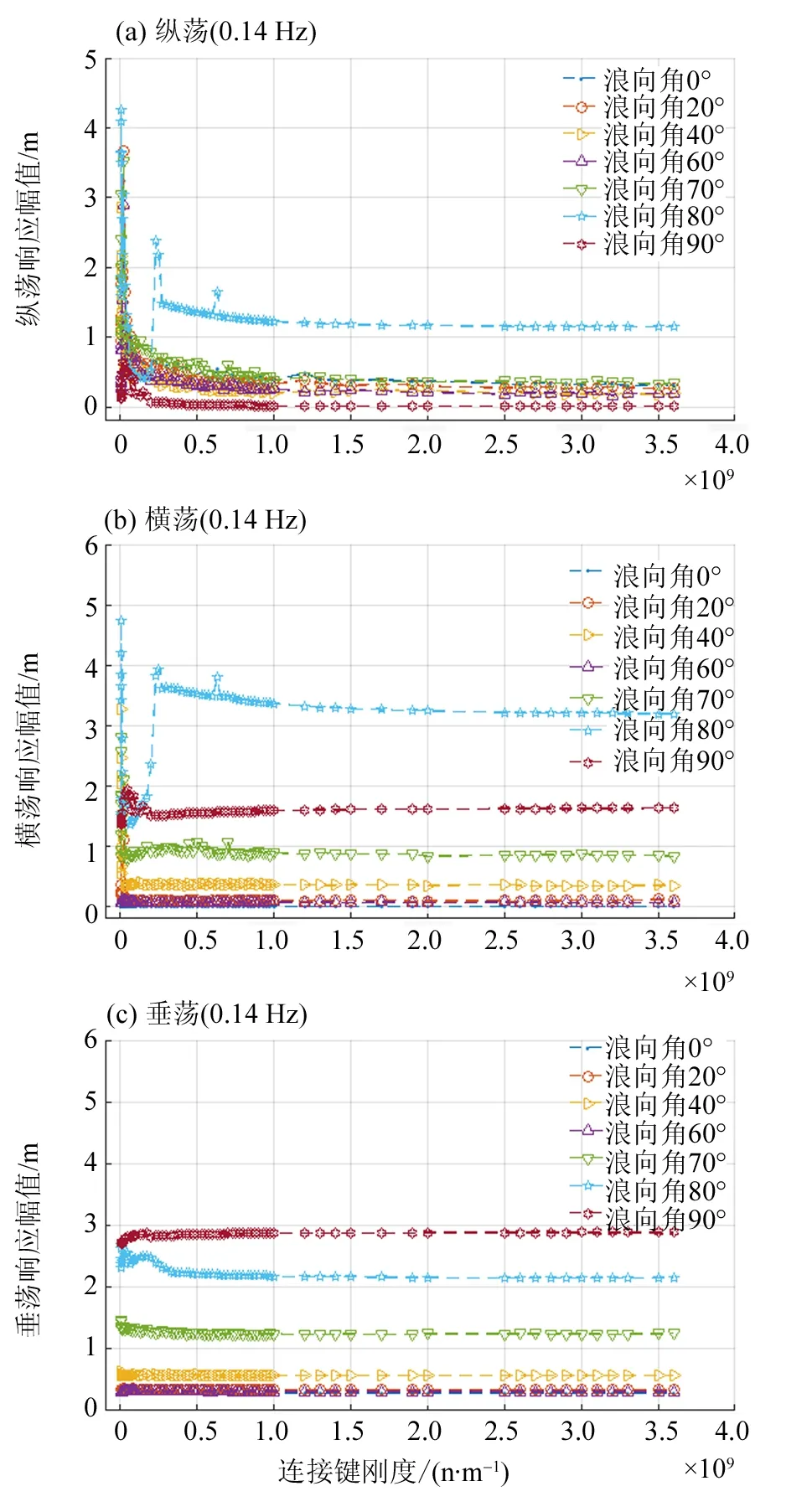
图4 波浪频率为0.14 Hz时模块M2响应幅值Fig.4 Maximum amplitude of module M2 in a wave frequency of 0.14 Hz

从图4可以看出，在高频f0=0.14 Hz的波浪条件下，当连接件刚度值大于2.35×107n/m时，模块纵荡、横荡、垂荡的响应幅值均趋于稳定。其中，在浪向角小于80°时，纵荡幅值保持在0.7 m以下，横荡幅值保持在1.7 m以下；而，浪向角等于80°时，纵荡的稳定幅值突增到1.46 m左右，横荡的稳定幅值突增到3.6 m左右；对比70°、90°时的纵荡与横荡，可见80°浪向角时发生的现象应当属于特定浪向下的弯曲共振。而对垂荡响应而言，其变化基本与幅值响应算子的变化保持一致，可见连接件在高频波浪条件下对模块垂荡的影响较小。

图5展示了在一个较低频率的波浪下的模块M2的位移响应幅值和结构中模块间连接刚度的变化关系。

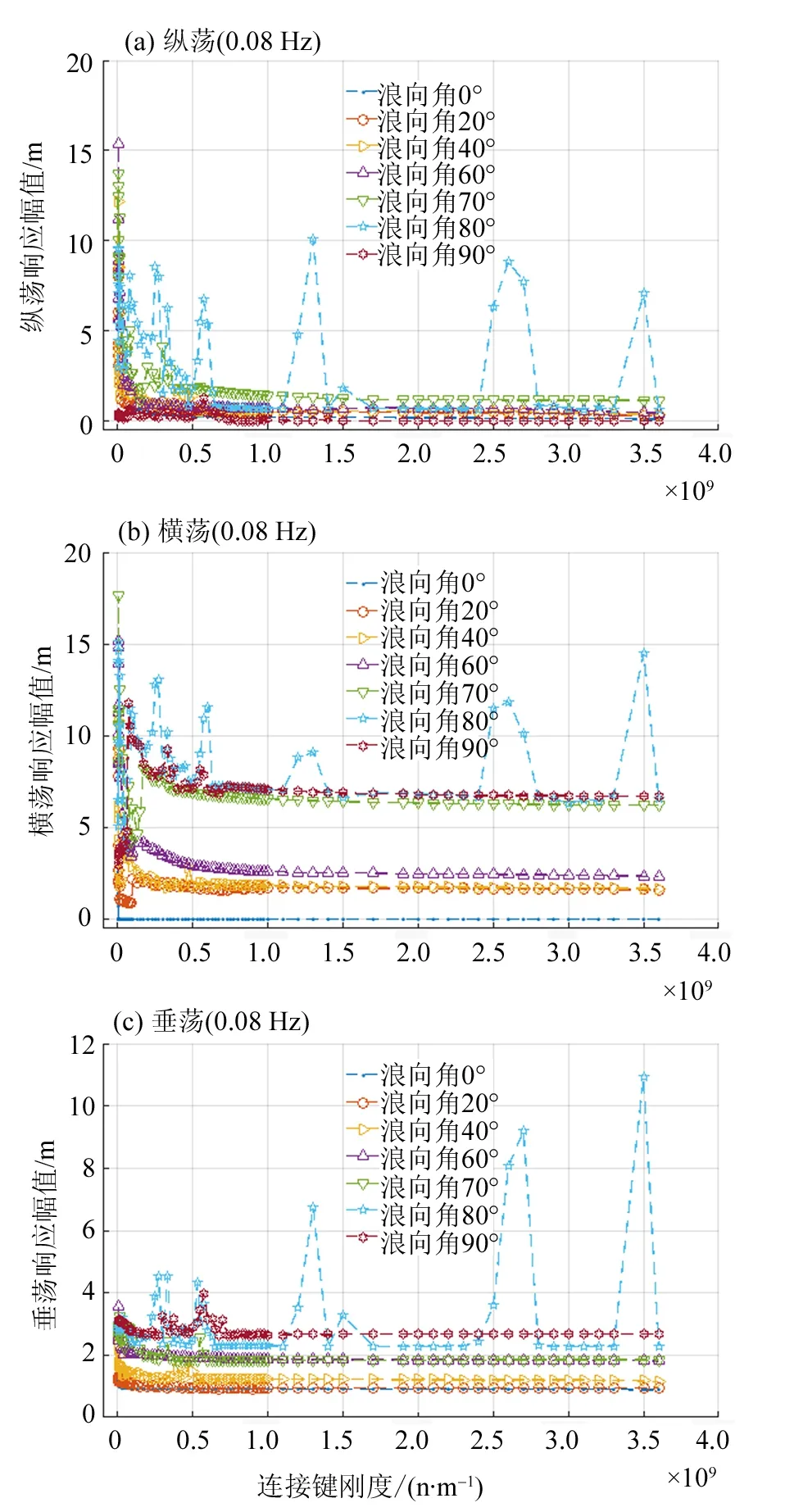
图5 波浪频率0.08 Hz时浮块M2响应幅值Fig.5 Maximum amplitude of module M2 in a wave frequency of 0.08 Hz

从图5可以看出，在低频值f0=0.08 Hz的波浪条件下，当连接件刚度值大于5.8×108n/m时，模块纵荡、横荡、垂荡的响应幅值均趋于稳定；在80°浪向角的条件下，随着刚度变化在特定的刚度区域出现了幅值跃升现象：当刚度处于1.2×109～1.8×109、2.45×109～2.8×109、3.3×109～3.5×109n/m区域时，浮块的纵荡、横荡、垂荡幅值均产生了明显的阶跃，其阶跃幅度达到周围值的2～4倍，这种特定区域的幅值阶跃现象是系统内部弯曲共振导致的结果。同时，在70°、90°浪向角下并未产生同样的现象，说明这种现象产生于特定浪向角附近。

从整体上看，浮式结构在不同频域不同浪向角下，表现出不尽相同的响应特性。而对比上述两个频段的响应状况，当浪向角达到80°时，即便在较高频波浪下的稳定响应幅值亦达到3.7 m，而在低频取值下的稳定响应可达到6.7 m且在特定刚度下有大幅阶跃。可见，在常见的近海波频范围内80°浪向角下，横荡响应幅值极可能稳定维持在3.7 m以上，长时段维持较大的位移幅度将产生较大的连接件内应力，这对结构安全构成较大影响。

4 结 论

本文使用网络化求解方法，针对一种简化的海上浮式平台进行了频域和时域求解，并得到以下结论：

1)通过对比幅值响应算子可以发现，随着浪向角的增大，三自由度下的幅值响应频区都相应扩大，从而使得改变固有频率获得较小响应更加困难。而通过对波浪力算子的求解可知，波浪力算子的变化在高、低频时随角度变化的趋势不完全相同。高频下波浪的绕射效应影响较为明显，在60°浪向角时出现了极小值。而低频下横荡和纵荡方向此参数上升，这说明高频下一阶和二阶波浪势耦合作用体现明显，而低频波浪下一阶波浪正压力起到主要作用。

2)比较两个不同频值下的浪向角-刚度-响应幅值情况，可以发现：在浪向角小于60°时，高频和低频下模块的M2幅值响应均表现得较为收敛；大于60°浪向角时，低频由于波浪力增大较快，其响应幅值上升较为明显。高频情况下，在浪向角80°时，在较高刚度下产生了阶跃，刚度增加到2.35×107n/m以后响应幅值阶跃至3.6 m左右，然后缓慢下降；低频时，在0.08 Hz条件下刚度值较高的某些区域内生了幅值阶跃，阶跃幅值达到周围稳定区域的2倍以上。因此，80°时的模块幅值响应缺乏稳定性，且在高刚度下亦可能发生明显的幅值阶跃现象。

3)在近海多体浮式平台的波浪响应中，最危险的状况表现在横浪时刻。在80°浪向角时，无论是低频还是高频波浪条件下都表现出远大于周边条件的响应幅值；尤其是低频波浪下，即使调高刚度亦有可能落入幅值阶跃区域，而在其附近的其他浪向角情况下并没有这种性质，这可能是一个由结构本身决定的特殊角度。由于海域波频范围和浪向范围是可以通过长期观测而进行评估的参数，在浮式平台建设时可以适当考虑其定位，以避免平台遭遇共振浪向角的情况而出现危险状况。