基于单井敏感性区域的油藏模拟辅助历史拟合

刘伟,赵辉,曹琳,张凯

(1.长江大学石油工程学院,湖北 武汉 430100;2.中国石油大学(华东)石油工程学院,山东 青岛 266580)

0 引言

油藏数值模拟历史拟合是油藏数值模拟中的关键环节,为油藏未来开发动态预测和开发方案制定提供正确模型[1-3].传统人工历史拟合速度慢,准确性低.若依赖于油藏工作者对油藏的分析认识和拟合经验,就无法满足油田开发高效化、实时化的要求.油藏模拟辅助历史拟合是基于最优化理论,并借助计算机实现对油藏模型参数的自动调整,相比于人工历史拟合,可以极大地提高拟合效率和模型的准确度[4-6].

历史拟合通常是在一定网格区域内调整模型参数,得到准确的单井敏感性区域,能提升历史拟合质量.单井敏感性区域是划定一个临界区域,认为单井的生产动态数据只与临界区域内网格的模型参数存在相关性,临界区域外的网格对生产动态数据没有影响[6-8].人工历史拟合是基于已有的油藏认知或以往经验,划定一个不精确的区域.在辅助历史拟合研究中,研究者通常基于地质信息(如沉积相态等),结合距离截断方法[6-8]得到单井敏感性区域,但距离截断存在一定的人为因素,不够准确.另外,历史拟合需要反演的油藏模型参数通常数以十万计,应用主流无梯度优化算法[9-12]的计算代价大.参数化[13-15]是一种提高计算效率的途径,其依据特定方式对油藏模型重新参数化,以减少模型参数的数量.

Fast-Marching Method(FMM)是一种可以快速高效追踪边界运移情况的方法,Sharifi等[16]应用FMM来标定油藏中单井控制储量.本文将FMM引入历史拟合单井敏感性区域的确定中,充分考虑油藏模型静态参数信息,准确获得单井敏感性区域,且不需要进行油藏模拟计算,网格计算效率高.获得单井敏感性区域后,提出一种简单的参数化方法,将单井敏感性区域内模型参数的平均值,作为历史拟合目标函数中的参数变量,极大降低了变量的维数,提高了计算效率.

1 单井敏感性区域定量表征方法

FMM是通过求解波动传播问题的程函方程获知边界的运移,程函方程的一般形式为

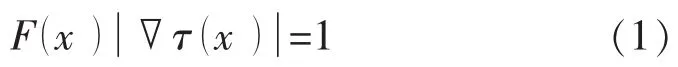
式中:F为速度,cm/s0.5;τ为飞行时间,s0.5;x为飞行空间位置.

在油藏多孔介质中,井点处油藏压力传播方程也可以表示为程函方程的形式[17],在静态地质参数场下,可利用FMM追踪计算压力波从井点穿过每个网格的飞行时间,利用追踪的飞行时间划定油藏三维单井敏感性区域.

对于油藏网格系统,假设油藏综合压缩系数和流体黏度是常数.压力波穿过每个网格的速度定义为

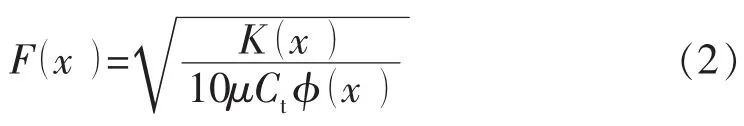
式中:K为渗透率,μm2;μ为流体黏度,mPa.s;Ct为油藏综合压缩系数,MPa-1;φ为孔隙度.

考虑油藏的非均质性,基于逆风差分近似求解程函方程,计算飞行时间的方程为

其中

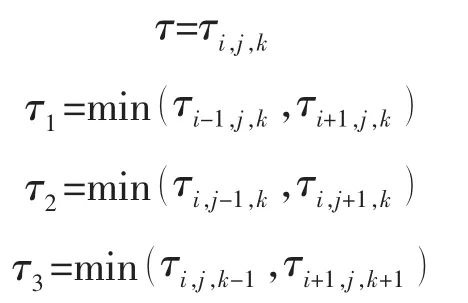
式中:Fx,Fy,Fz分别为网格x,y,z方向上的速度,cm/s0.5;Δx,Δy,Δz分别为 x,y,z方向上的网格尺寸,cm;i,j,k分别为油藏模型网格体系中x,y,z方向上的坐标.

以二维非均质油藏模型为例,油藏网格飞行时间的追踪过程如图1所示.

1)将某一确定网格作为初始起点(τ=0),标记为冻结点(红色网格)(见图1a的网格13).

2)找到与冻结点相邻的网格,标记为相邻点(绿色网格)(见图1b的网格8,12,14,18).

3)利用式(3)计算压力波从冻结点到达相邻点的飞行时间,选出飞行时间值最小的相邻点,标记为冻结点(见图1c的网格12).

4)将网格12作为新的初始起点,并找到网格12的相邻点(不包括已经计算过飞行时间的网格)(见图1d的网格7,11,17).

5)计算压力波从网格12到达网格7,11,17的飞行时间,并找到所有相邻点中飞行时间值最小的点,标记为冻结点(见图1e的网格18).

6)重复步骤4)-5),直到所有的网格被标记为冻结点(见图1f).

图1 飞行时间追踪过程示意

在计算整个油藏网格的飞行时间过程中,通常将井点处网格作为初始起点.离井点越近,飞行时间值越小;离井点越远,飞行时间值越大.确定单井敏感性区域的具体处理方法为:当油藏存在多口井时,每一个网格对每口井会得到不同的飞行时间,选出最小的飞行时间值,将该网格划归于最小飞行时间值所对应井的敏感性区域;基于得到的单井敏感性区域,将区域内油藏模型参数的平均值,作为历史拟合目标函数中的变量元素,不以单个网格的模型参数为变量反演对象.

2 历史拟合数学模型及优化求解

2.1 数学模型的建立及油藏模型的参数化

以拟合历史动态生产数据为目标,历史拟合目标函数定义为[11]

变量u的元素包含孔隙度、渗透率、饱和度等油藏模型参数,向量dobs的元素包含压力、含水率、产油量等历史动态生产数据.对于油藏模拟历史拟合问题,本质是利用最优化方法求解变量u,使得目标函数Z()u取得最小值.

对于实际油藏历史拟合,以单个网格的模型参数为反演对象,变量u的维数巨大.本文提出一种近似的参数化方法,采用单井敏感性区域内网格模型参数的平均值,作为变量u的元素.由于油藏模型参数在每一层存在差异,因此模型参数的平均值是对每一层的敏感性区域进行计算.变量u的维数仅与油藏井数、油藏模型的纵向层数和反演参数的种类数有关,与油藏模型的网格数量没有关系.参数化后,变量维数极大降低,计算效率提高.

依据拟合前后单井敏感性区域内网格模型参数平均值的倍数变化关系,更新油藏模型参数,以孔隙度为例,参数化公式为

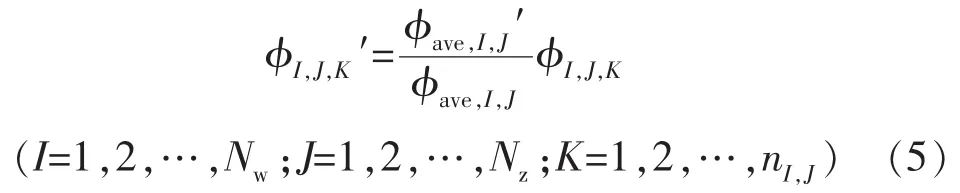
式中:φI,J,K,φI,J,K′分别为拟合前、后第I井敏感性区域内第J层中第K个网格的孔隙度;φave,I,J,φave,I,J′分别为拟合前、后第I井敏感性区域内第J层中网格孔隙度的平均值;Nw为总井数;Nz为油藏模型纵向层数;nI,J为第I井敏感性区域内第J层的网格总数.

2.2 近似扰动梯度升级算法

本文采用赵辉等[18]提出的近似扰动梯度升级算法,对历史拟合目标函数进行优化求解,该方法是目前常用历史拟合算法SPSA的一种改进算法.对于目标函数Z(u),考虑在第l个迭代步的最优模型参数变量为ul,在其周围进行扰动生成N个模型参数变量:

式中:ul,i为第l步第i个模型参数变量;γ为扰动步长;Ll,i为服从某分布的扰动向量.

式中:L为N个扰动向量组成的矩阵;ΔZ为N维向量;a为常数;M为一个N维下三角矩阵.

向量ΔZ的元素为模型参数变量ul,i对应的目标函数值与当前最优目标函数值的差值.另外,当Ll,i服从伯努利分布,M为单位矩阵时,式(7)即是SPSA算法的梯度计算公式.

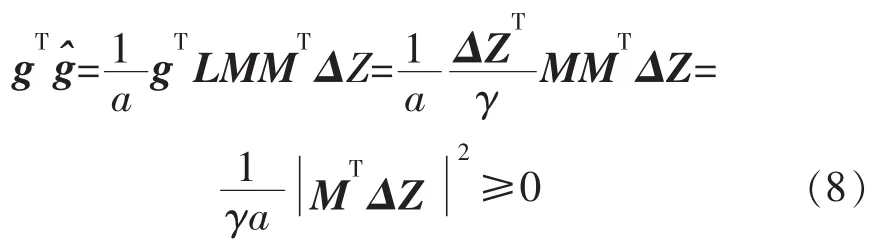
由于式(10)中除M外都为确定量,不牵涉油藏模拟器运算,可以使用传统的优化算法[19]对其进行优化迭代,如拟牛顿法.每个迭代步都对M进行优化,然后采用优化后的M构造梯度,这样得到的梯度更加接近真实梯度.获得近似扰动梯度后,更新模型参数变量:

式中:ul+1为第l+1迭代步参数向量;ul为第l迭代步参数向量;αl为迭代步长;为的无穷范数.

3 实例应用

运用本文提出的方法对某碳酸盐岩油藏进行了历史拟合测试.该油藏非均质性极强,油藏模型网格划分为76X115X20,总网格数为174 800,共有油水井29口.拟合的历史动态生产数据是油藏生产4 564 d的区块累计产油量和单井日产油量,反演的油藏模型参数为渗透率和孔隙度,参数化后变量的维数为1 160.油藏模型第1层网格飞行时间的计算结果见图2,根据飞行时间确定第1层单井敏感性区域(见图3).

图2 第1层网格飞行时间

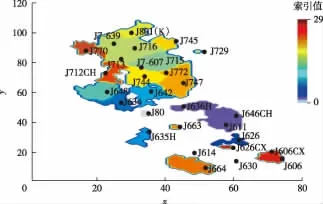
图3 第1层网格单井敏感性区域

历史拟合目标函数优化结果如图4所示,在经过约35次迭代步后,目标函数逐渐收敛.油藏的区块累计产油量和单井日产油量拟合结果如图5、图6所示,拟合后模型的生产数据较拟合前更接近实际值,拟合效果好.从历史拟合前后油藏模型第1层网格渗透率场分布可以看出,拟合前后渗透率变化较大(见图7、图8).图中渗透率取对数值.

图4 目标函数优化结果

图5 区块累计产油量拟合结果

图6 单井日产油量拟合结果

图7 第1层网格拟合前平面渗透率

图8 第1层网格拟合后平面渗透率

4 结论

1)针对历史拟合中单井敏感性区域的确定,基于油藏中压力传播方程,采用FMM求解其程函方程,提出了定量表征油藏中单井敏感性区域的计算方法.该方法可以快速准确地确定油藏三维单井敏感性区域,具有稳定性好、计算效率高的优点,且适用于大型实际油藏.

2)针对实际油藏应用中历史拟合目标函数的参数变量维数大的问题,提出以油藏各层中单井敏感性区域内网格模型参数的平均值作为历史拟合目标函数中参数变量的元素,大幅度降低了参数变量的维数,提高了计算效率.

3)油藏测试结果表明,基于FMM确定的单井敏感性区域,采用近似扰动梯度升级算法,对油藏区块和单井动态生产指标的拟合取得了较好的效果,验证了本文提出方法的可靠性.