跳出三角函数中的范围陷阱
2018-12-04潘梅耘
潘梅耘
三角函数范围问题是高考中的热点问题,也是困扰同学们学习的一个难点问题.本文就三角函数中典型的范围易错题加以评析,并给出相应的解题对策,以期达到窥一斑而知全豹的功能.
一、三角函数值对角范围的隐限制
角终边的唯一性决定了角的某一三角函数值是唯一的,但角的某一三角函数值对应角大小因有终边相同形式或终边的对称性,从而具有多解性.在一定范围内,对应角受到限制,需要取舍.如果角的范围仅仅考虑明示条件,不注意隐含条件的挖掘,处理不到位,就会引起增解,掉入陷阱.
案例1已知,且α,β∈(0,π),求2α-β的值.
错解由题tan(2α-β)=tan[2(αβ)+β],因为,所以
剖析以上解法过程中,仅考虑α,β的明示范围,未注意条件以及推论与明示范围相结合,推知角α,β的值应是唯一的.事实上由,知β角是唯一确定的钝角(查表可得具体值),如求出同理推知α角也是唯一确定的,从而2α-β的值应是唯一的,只要适当限制α,β的范围,就能达到预期的效果.
正解得到(*)后:由知.由,知.所以所以
反思在利用三角函数值求角的问题时,角的范围会对角的取舍有决定性的影响.一般地,求角时先求该角的某一个三角函数值,然后确定该角的范围.如果在题目给出的明示条件下,求出的该角的范围内,所求角是唯一的,往往不会出现增解,但如果所求角不唯一,就要进一步考虑影响角范围的一些隐含信息了,直至确信解的个数为止.
解答此类问题尽管不太容易,但还是有一些对策的,举例如下:
对策一:恰当选择三角函数名称,避免增根的出现
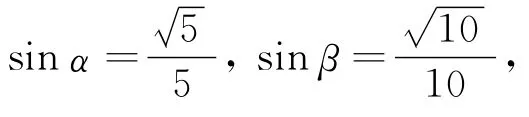

评析本题采用了求余弦值的方法,因为在α,β为锐角的情况下,0<α+β<π,此时余弦值在第一和第二象限异号,和角是一一对应的.本题若改用正弦求,则有:,由α,β为锐角得0<α+β<π,此时或,还需要对角的范围作进一步的限制才行.由,结合α,β为锐角得所以所以
对策二:利用三角函数值的正负性、单调性,限制相关角的范围和确定值的取舍
例2已知,求sinx.

二、三角形中量的联系对角范围的隐限制
三角形成立的前提、多变量之间的约束,以及实际生活等背景,给角的范围蒙上了一层纱,使同学们防不胜防,但只要不断积累和总结、归纳和反思就能起到加深理解、熟能生巧的效果.
案例2在锐角△ABC中,若C=2B,则的范围是________.
错解由题所以的范围是(0,2).
剖析主要是求B的范围时,未充分用好锐角三角形这一条件,根据条件中的锐角三角形,得知三角形的三个角都是锐角,应列出三个角都为锐角的三个不等式.
正解因为△ABC为锐角三角形,所以且且,所以,所以,所以的范围是
反思在解三角形中的三角函数问题时,能注意到用正、余弦定理将边角单一化,但三角形这个背景所暗示的前提条件常常被忽视,从而带来角范围的扩大.如果本题条件去掉“锐角”两个字,同学们是否仍能注意到0<A=π-B-2B=π-3B<π,且0<B<π,0<C=2B<π,从而这一范围条件?如改为“钝角三角形”,又如何求角的范围呢?对,需要对角A与角C哪个是钝角进行讨论.
解答此类问题常见对策有:
对策一:优先考虑三角、三边所有的限制条件,逐一转化为目标量的范围
例3已知三角形三边成等比数列,求公比的范围.
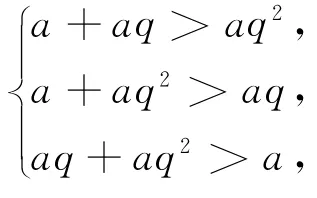
评析三角形存在的前提:任两边之和大于第三边要优先考虑,可避免范围出错,但可考虑优化.
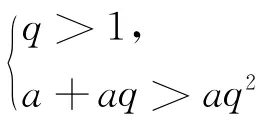
三边定序时,只要较小两边之和大于第三边就行;三边不定序时,可改为:任意一边介于另两边的差的绝对值与另两边的和之间.如三边为2,x,,求x范围,可列出不等式求解.
例4已知在锐角△ABC中,角A,B,C所对的边长分别为a,b,c,∠C=60°,当c=1时,求a+b的取值范围.

评析本题多数同学首先会想到利用余弦定理,得到边的关系a2+b2-ab=1,但不易将目标减元,更不便求边的范围.因角的范围便于求解,故考虑利用正弦定理将边化角求解.在三角形中,有关求范围问题,一般都是化边为角,再根据内角和定理,三个角的范围相互约束,当它们都用目标角表示时,这种隐含的约束范围才能揭示出来,否则就会出错.
对策二:不定三角形解情多,数形结合思范围
解三角形中有一类不定三角形,即已知两边及一边对角,其解的情形可由下表得知:

例5在△ABC中,a=x,b=2,B=45°,若三角形有两解,求x的取值范围.
解析由图知(图略)asinB<b<a,xsin45°<2<x,解得x的取值范围是
评析本题也可用余弦定理求解:在△ABC中,由余弦定理得b2=a2+c2-2accosB,即由题意,关于c的一元二次方程有两个正根,故Δ>0且x2-4>0且,解得x的取值范围是
应用余弦定理将问题转化为一元二次方程的实根分布,思路清晰.事实上可以证明:若已知a,b,A的值,由a2=b2+c2-2bccosA,化为c2-(2bcosA)c+b2-a2=0(*),Δ=4(a+bsinA)(a-bsinA),在a<b的前提下,当Δ>0时,三角形有两解;当Δ=0时,三角形有一解;当Δ<0时,三角形无解.当a<b时,以上结论与上表中第三大行的结论一致,当a≥b时,由方程(*)知c1c2=b2-a2≤0,说明方程(*)如有两解,其中必有一负一正或一零一正,实为一个有效解,也与上表中前两行结论一致.所以在对边小于邻边的前提下,用余弦定理求解,不必担心增解.
综上,我们可以看出三角函数值本身的正负性、绝对值大小就隐含着角的范围限制;多变量之间的约束、三角形成立的前提,以及实际生活的背景等也是产生范围限制的原因,但万事万物都有一个源头,只要抓住起因,坚持等价变形,充分挖掘隐含信息,揭示本质规律,就能驾驭“范围”这匹倔强的野马,越过重重陷阱,奔赴成功的乐园.
巩固练习
1.在△ABC中,已知a=1,A=30°,则S△ABC=________.
2.在△ABC中,边上的高则BC=________.
3.在锐角三角形ABC中,tanA=t+1,tanB=t-1,则t的取值范围是________.
4.已知△ABC中,,求cosC的值.
5.已知△ABC中,,求cosC的值.
参考答案

