“隐圆”发现之旅
2018-12-04郜杰翔
郜杰翔
最近我做到这样一道题目,思考了很多,很受启发.跟大家一起分享.
例已知△ABC的三边长为a,b,c,若a2+b2+2c2=8,则△ABC面积的最大值为________.
三角形面积的问题首先想到的是面积公式的选用,常用面积公式有和

图1
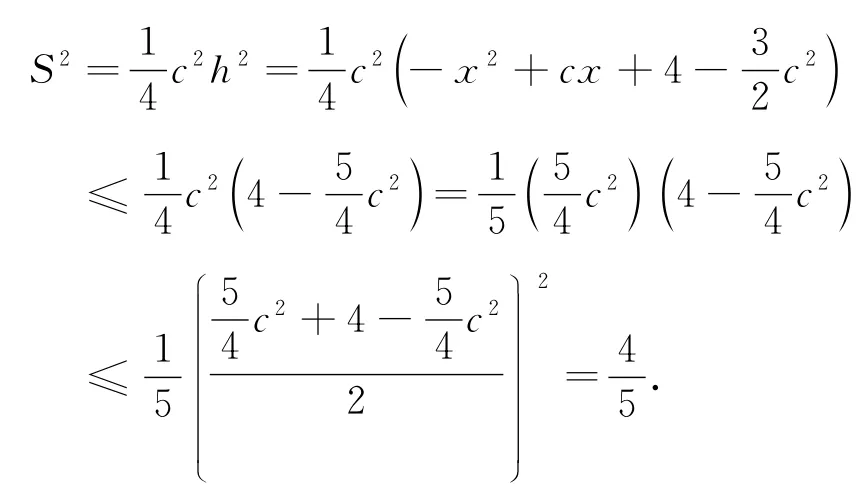
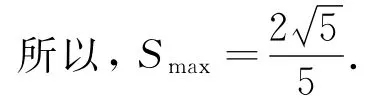
方法二:常规处理方法还有依据余弦定理c2=a2+b2-2abcosC和面积公式借助a,b对称的特征,进行适当的变形处理,可以得到S的取值范围:

此时,进一步求解的难度很大.作为填空题,在万不得已的情况下只能连蒙带猜.
由a,b对称,令a=b,

用这两种方法能得到结果确实都不容易,其实如果将条件a,b,c中的一个量看作是常量,那么条件就变得相对熟悉.例如将c看作常量,则有CB2+CA2=8-2c2,即动点C到两个定点A,B的距离平方和为定值,由此本题还有一种看似普通却非常神奇的做法——解析法.
方法三:以边AB的中点O为原点建立平面直角坐标系xOy,

注:本解法先将c视作常数,然后进行求解.
【课本探源】
(苏教版选修2-1P.64习题2.6(2)第1题)已知线段AB长为2,动点M到A,B两点的距离的平方和为10,求M的轨迹方程.
这道课本题,相信同学们都能自如地运用解析法求解.我们不难发现上述模拟题可以转化为:
已知线段AB长为c,动点M到A,B两点的距离的平方和为8-2c2,求M的轨迹方程.
【构建模型】
从上述研究中,不难发现如下结论:
若线段AB长为定值,动点M满足MA2+MB2=λ(λ为定值),则M的轨迹为圆.
特别地,当λ=AB2时,M的轨迹为以AB为直径的圆.
【本质探索】
那么为什么“线段AB长为定值,动点M满足MA2+MB2=λ(λ为定值),则M的轨迹为圆”呢?
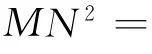
【模型应用】
1.已知A,B为平面内的两个定点,且AB=2.若在平面内存在唯一一点P同时满足:①,②PA2+PB2=λ(λ∈R),则λ的取值集合为____________.
答案:
分析:该题条件①属于我们所熟悉的阿波罗尼斯圆,如果知道条件②也可以转化为圆,题目就变成了圆与圆的位置关系问题,利用几何关系巧妙得解.
2.已知圆O:x2+y2=4,点P(0,1),圆上的两动点A,B满足PA⊥PB,AB的中点记为M,则PM的取值范围为________.
答案:
分析:这道题看似无从下手,实际上也只是上述模型的变形而已.
由题意知,该题的定点是O,P两点.
根据圆的性质,OM2+MA2=OA2=4.
又△APB是直角三角形,M是斜边AB的中点,所以MP=MA.
所以OM2+MP2=4.即上述模型,从而巧解上述问题.
总结在考查上述模型时,命题人总会想方设法将条件进行“着装打扮”,隐藏我们熟知的圆,这就需要我们揭开题目“神秘的面纱”探索本质.
【模型推广】
1.如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ.若,则△PAC的面积的最大值为________.
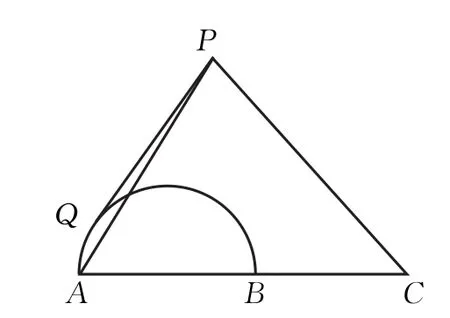
图2
答案:
而PQ2=OP2-1,
则PC2=2OP2-2,即2PO2-PC2=2.
思考:此时O,C均为定点,动点P满足上述关系式时,其轨迹是圆(或半圆)吗?
通过求轨迹方程的一般步骤不难得出,答案是肯定的.
由此得出
分析:这道题难住了很多同学,他们在考虑三角形面积如何表示时陷入了僵局.然而这个题目里也隐藏着一个美妙的圆.
记半圆的圆心为O,则OQ⊥QP.
推论1若线段AB长为定值,动点M满足αMA2+βMB2=λ(λ为定值且α+β≠0),则M的轨迹为圆.
只要以AB中点为坐标原点,运用解析法就可以证明此推论.
2.(2017年江苏高考卷第13题)在平面直角坐标系xOy中,A(-12,0),B(0,6),点P在圆O:x2+y2=50上,若,则点P的横坐标的取值范围是________.
答案:
分析:尽管条件中线段AB长仍为定值,但另一条件却变成了.我们先退一步想,动点P满足时,其轨迹是圆(或半圆)吗?
答案也是肯定的!

又AB是定值,可得|AP|2+|BP|2=220是定值,
则该模型又回到了最初的模型.
由此得出
推论2若线段AB长为定值,动点M满足(λ为定值),则M的轨迹为圆.
特别地,当λ=0时M的轨迹为以AB为直径的圆.
此推论可用求轨迹方程的基本方法证明,且本质与原先的模型相同.
【模型启示】
许多试题的命制思路都是从同一类式子出发,本质都是一样的,只是表达的形式不尽相同.这就要求我们学会“透过现象看本质”,应对复杂问题才能挥洒自如.
