体外预应力混凝土风力发电塔地震易损性分析

2018-12-04曹雨奇阳荣昌刘慧群

同济大学学报（自然科学版） 2018年11期

曹雨奇，阳荣昌，刘慧群，舒展

(1. 同济大学土木工程学院，上海 200092； 2. 同济大学建筑设计研究院(集团)有限公司，上海 200092)

风电是世界各国实现非化石能源发展目标的最重要的可再生能源之一.风力发电结构设计规范(IEC[1]、DNVGL[2]等)主要应用于北欧等低地震烈度地区，然而越来越多的风场在北美、东亚等高地震烈度地区投入建设.虽然风荷载可能依旧是风力发电塔结构设计中的控制性荷载，但是风力发电塔在地震作用下发生损失的风险还是存在的.风力发电塔对灾害敏感性较其他结构高，主要原因是：风力发电塔冗余度低，结构等效于一根悬臂梁，任何一处截面的破坏都对整体结构产生致命影响；在一个风场内，各风力发电塔设计相同或类似，缺乏多样性，在灾害作用下有可能发生大范围破坏.因此，对风力发电塔进行抗震性能分析具有一定的重要性和紧迫性.

风力发电塔按照建造材料主要分为钢筒塔和混凝土塔两大类.许多学者对风力发电塔抗震性能的研究多集中于钢筒塔.Nuta等[3]对1台处于停机状态的1.65 MW钢筒塔进行了地震易损性分析，得到了该类塔弯曲屈曲的破坏模式，并指出该类塔地震破坏风险较小.由于风力发电塔结构本身超越弹性极限就接近破坏，以及风力发电塔越建越高的发展趋势，抗震分析在设计中显得愈加重要.Patil等[4]对强震作用下1座80 m轮毂高度的钢筒塔进行了易损性分析，定义了4种极限状态，并指出基础倾覆、筒壁屈服、永久变形、整体屈曲的破坏递进性.Sadowski等[5]以1台70 m轮毂高度的钢筒塔为例，对存在几何缺陷的风力发电塔进行了地震分析，发现几何缺陷显著提高了风力发电塔对地震作用的敏感性.

在我国，为解决风电消纳问题，风场分布由三北地区向中东部低风速区转移.高风塔是低风速区风能开发的必然选择.高风塔对结构的强度和刚度提出了更高要求.与传统钢筒塔相比，混凝土塔具备的最大优势在于刚度较大.为避免自振频率与风机运行频率(叶片旋转频率1f和叶片通过频率3f，f表示频率)重合引发共振，风电支撑结构设计一般有自振频率大于3f的刚-刚方案、介于1f和3f之间的柔-刚方案和小于1f的柔-柔方案.低风速区钢筒塔一般只能采取柔-柔方案，而混凝土塔则可以采用更优的柔-刚方案.混凝土塔刚度大，机舱在相同风荷载下更平稳，增加了发电时间和发电量.混凝土塔还具有造价低、耐久性好、阻尼特性好、不存在局部失稳以及中间没有连接从而使运营维护成本降低等优势.近年来混凝土塔逐渐受到关注并得到了一定的应用.

以混凝土为主要材料建造的风力发电塔比传统钢筒塔重数倍，因此在相同外部条件下承受的地震作用显著增大.随着高地震烈度地区风能开发的推进，地震作用在某些情况下将成为控制荷载，因此对混凝土风力发电塔进行抗震分析很有必要.然而，由于当前混凝土风力发电塔应用相对较少，现阶段针对混凝土风力发电塔抗震性能的研究还不够多.Ma等[6]采用规范反应谱法和时程分析法分析了1座轮毂高度120 m额定功率5 MW的体内预应力混凝土风力发电塔的地震响应，讨论了阻尼比和地基刚度对地震响应的影响.周长东等[7]分析了性能类似的混凝土烟囱的地震易损性.

本文以某额定功率3 MW、轮毂高度120 m的体外预应力混凝土风力发电塔为研究对象，采用开源程序OpenSees，基于分布塑性的纤维梁柱单元建立非线性有限元模型.选取20条真实地震记录，进行了增量动力分析(IDA)，并建立了概率地震需求模型。定义了损伤状态限值并形成了体外预应力混凝土风力发电塔的地震易损性曲线，对发电塔易损性进行分析和评估，以考察其在不同地震烈度区域的适用性.现有研究[8]表明，风荷载对风力发电塔地震易损性的贡献不甚明显，因此在分析过程中假定风机处于停机状态，并且不考虑风荷载作用.

1 体外预应力混凝土风力发电塔设计

在混凝土塔外形的选择上，单一直径的混凝土直塔筒模板费用低且结构效率也较低，混凝土锥形塔筒虽然可提高结构效率，但是其模板费用过高.分阶变径预制体外预应力混凝土风力发电塔[9]可以较好地在模板费用和结构效率上取得平衡.另外，体外预应力钢绞线环向分布在混凝土筒壁内侧，避免了体内预应力方式逐段穿钢绞线的困难，有利于提高施工效率，同时钢绞线外露方便进行监测和维护.塔体的构形如图1所示.

图1 体外预应力混凝土风力发电塔示意图Fig.1 Diagram of external prestressed concrete wind tower

本文以某拟建于7度设防区的体外预应力混凝土风力发电塔为研究对象.根据地勘报告，场地类别为Ⅲ类，设计地震分组为第三组，设计基本地震水平加速度峰值为0.10g，特征周期为0.77 s.机组额定功率为3 MW，顶部机舱、轮毂和叶片的总质量为172 t.

混凝土风力发电塔总高118 m，其中下部105 m为预制混凝土塔筒，顶部13 m为钢筒.预制混凝土每段高度约为3.1 m，环形截面主要规格从下到上分别为Φ8 000 mm×350 mm、Φ6 600 mm×350 mm及Φ4 500 mm×400 mm，对应高度分别为27.7 m、30.8 m及24.6 m，不同规格截面之间设置2节过渡段连接，过渡段高度约为6.2 m.钢筒底部截面为Φ4 200 mm×18 mm，通过高度为1.6 m混凝土转接段与底部混凝土塔筒连接.各节配置内外2圈纵向受力筋(非预应力筋)，保护层厚度50 mm，主要截面的配筋面积如表1所示.混凝土筒内部环向均匀布置16股钢绞线，钢绞线在从下往上第2个过渡段位置有约1°转折.

混凝土筒段与筒段之间抹灰找平.每股钢绞线截面积2 660 mm2，施加预应力3 200 kN，确保混凝土部分在正常使用工况下全截面受压.由于部分结构采用钢结构，阻尼比按4%估计.

表1 主要截面纵向受力筋配筋情况Tab.1 Placement of longitudinal reinforcement in major sections

2 有限元模型

根据设计资料，采用OpenSees建模.体外预应力混凝土风力发电塔的计算模型采用底部固结的悬臂梁.采用基于柔度法的分布塑性纤维梁柱单元对塔筒进行离散.与分段一致，在混凝土塔筒的高度方向上每3.1 m划分一个单元，每单元设置5个积分点.过渡段采用等截面圆筒进行简化，其外径和壁厚分别取该过渡段顶部和底部实际截面外径和壁厚的平均值.每个单元截面混凝土部分离散为600个纤维(圆周方向120个，径向5个)，纵向主钢筋根据实际数目、面积、位置建立相应纤维.忽略截面弯曲、拉伸与剪切的耦合及剪切非线性，利用OpenSees的Section Aggregator命令对截面进行聚合，实现对截面剪切、扭转的模拟.

采用桁架单元对钢绞线进行模拟.通过设置钢绞线材料的初始应力实现预应力的施加.为模拟钢绞线与混凝土塔筒的相互作用，在混凝土塔筒顶部钢绞线锚固位置和中部钢绞线与混凝土过渡段接触位置各设置16个钢绞线桁架单元的节点，在顶部用弱刚度弹性梁柱单元将混凝土塔筒顶部节点与16个钢绞线顶部节点连接，并约束这17个节点的3个平动自由度；类似地，在钢绞线转折处用弱刚度弹性梁柱单元将中心混凝土塔筒节点与附近的16个钢绞线节点连接，约束这17个节点的x向和y向平动自由度，但允许z向出现相对位移，如图2所示.这样可以达到钢绞线随混凝土塔筒协同变形的效果，同时不影响钢绞线因混凝土塔筒变形而在筒壁内的滑动.由于在混凝土筒壁外部设置钢绞线，因此钢绞线的预紧力会使筒壁外侧受拉、内侧受压.采用梁柱单元无法反映这种作用.根据圣维南原理，随力的传递，截面上的预压力将趋于均匀.实体建模的有限元分析结果显示，锚固点下1倍直径范围外截面上的预压力已分布均匀，因而在OpenSees中采用梁柱单元对整体结构进行建模分析是可行的.混凝土塔筒的质量离散到各节点上，顶部机舱、轮毂和叶轮的质量设置在对应重心位置的节点上，并通过刚度大的弹性梁柱单元与风力发电塔顶部节点连接.模型中不计钢绞线质量.

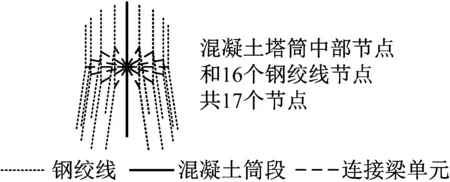
图2 钢绞线与混凝土塔筒相互作用建模示意图Fig.2 Diagram of strand-tower interaction modelling

由于预制段与预制段之间仅通过抹灰找平，同时钢筋不连续，因此不考虑混凝土和钢筋2种材料的受拉强度.选取Kent-Scott-Park单轴材料模型(Concrete01)作为混凝土的本构关系模型.受约束混凝土考虑了约束箍筋对混凝土强度和极限应变的提高作用，保护层按无约束混凝土材料考虑.对于外围保护层混凝土，考虑到在强震作用下可能发生脱落或压碎，故取保护层混凝土极限抗压强度为零.钢筋的本构模型在原有Giuffre-Menegotto-Pinto模型(Steel02)基础上，采用uniaxialMaterial Series命令将钢筋材料与刚度极大的只压不拉材料(ENT)“串联”(应力相等，变形叠加)，实现了钢筋的只压不拉特性.原有钢筋材料和新定义的钢筋材料的本构曲线对比如图3所示，应力σ和应变ε均以受压为正.材料模型所需参数取值如表2和表3所示.整体有限元模型如图4所示(为便于显示，图中只给出2根钢绞线，实际为16根).

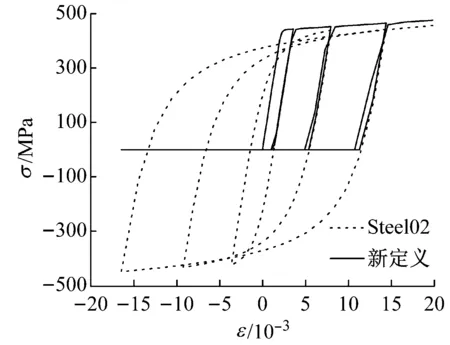
图3 Steel02本构与新定义本构对比Fig.3 Comparison between original constitutive model and custom one

为验证建模的正确性，对模型进行模态分析，结构的前6阶模态分析结果如表4所示.

表2 混凝土材料性能Tab.2 Material properties of concrete

表3 钢筋材料性能Tab.3 Material properties of rebar

a 结构示意图b OpenSees计算模型c 主要截面

图4体外预应力混凝土风力发电塔三维有限元模型(单位：mm)

Fig.4Three-dimensionalfiniteelementmodelofexternalprestressedconcretewindtower(unit:mm)

3 地震动的选取

采用美国太平洋工程地震研究中心数据库(PEER)中的地震记录作为IDA的地面运动输入.将地震缩放系数控制在0.5～2.0范围、矩震级在6.5～8.0范围、震中距在15～80 km范围.根据输入地震动的反应谱在周期0.05～3.00 s(约为结构第1阶自振周期的0.025～1.500倍)范围内拟合设计反应谱的原则，从数据库中挑选了20条实际地震记录，如表5所示.所选取的地震动平均反应谱与规范谱的比较如图5所示.可见，在周期0.05～3.00 s范围内，所选地震动的平均反应谱与规范谱吻合较理想.

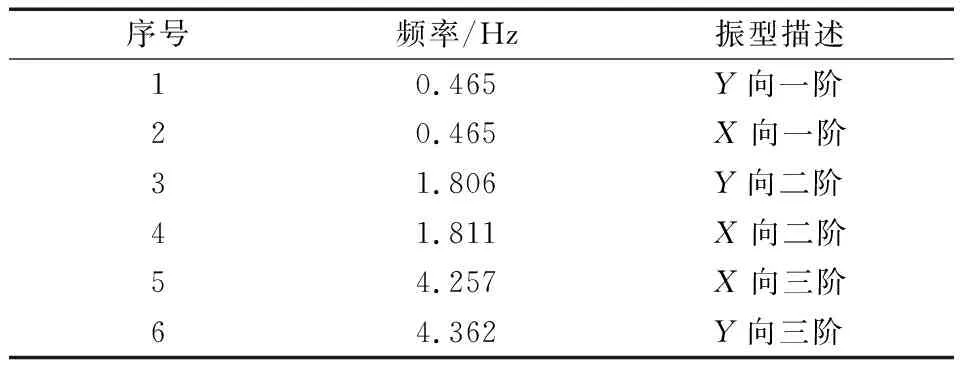
表4 模态分析结果(前6阶)Tab.4 Modal analysis results(the first six modes)

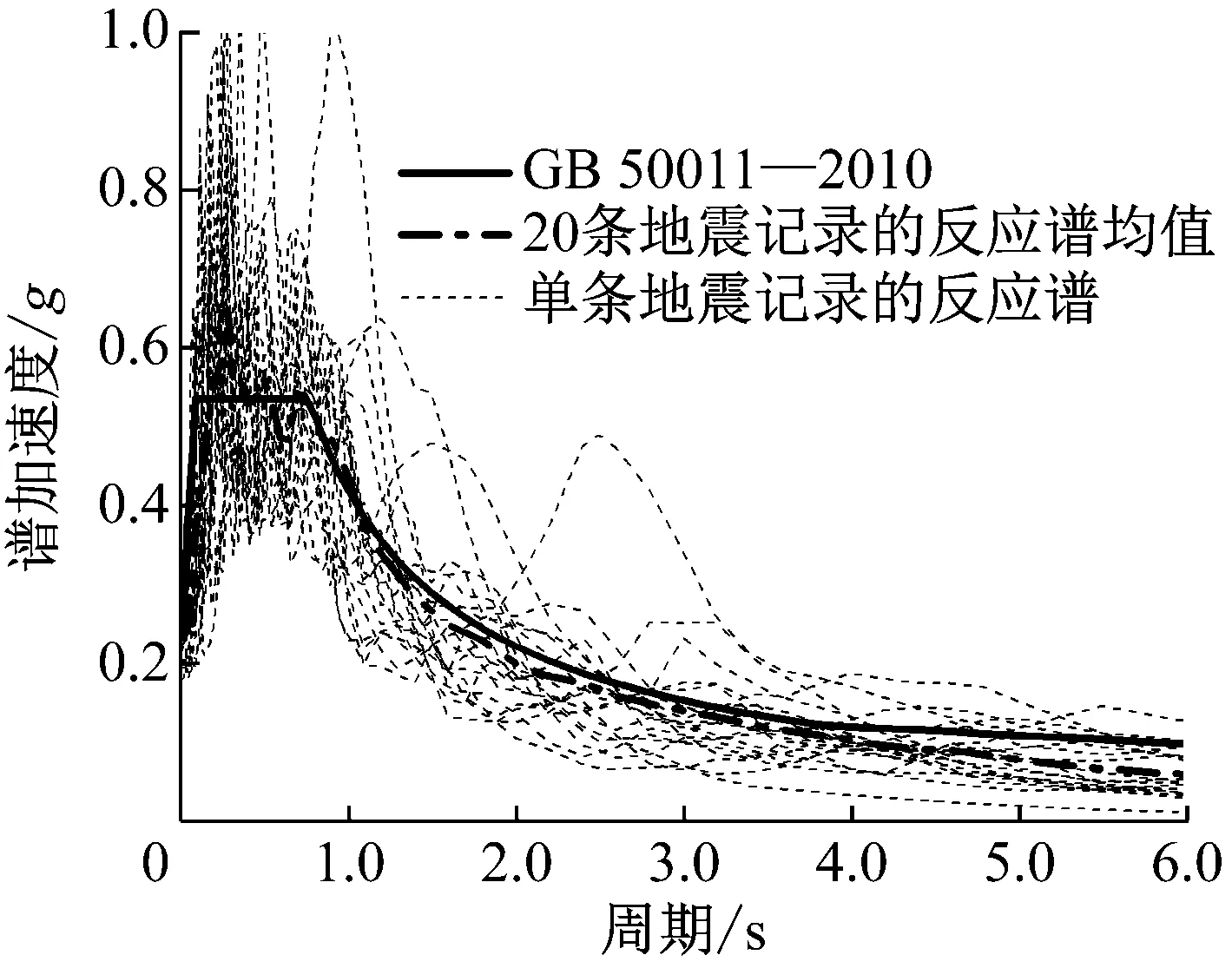
图5 所选地震记录的平均反应谱Fig.5 Mean response spectra of the selected input ground motions

4 结构增量动力分析

4.1 地震动强度参数的确定

峰值地面加速度具有简单直观的特点，同时也是现行GB 50011—2010《建筑抗震设计规范(2016版)》[10]推荐的时程分析强度参数，因而在本文中选取峰值地面加速度作为地震动强度参数.

4.2 结构需求参数的选取

为掌握结构的破坏机理和非线性变形特征，进而确定极限状态，在进行IDA前对本塔进行pushover分析.根据之前的模态分析结果，以一阶模态荷载模式施加荷载.由于前二阶模态Y向频率略微低于X向，选择Y向作为加载方向，在下文的IDA中，也将Y向作为地震动的输入方向.风力发电塔顶部位移随底部剪力变化的荷载位移曲线如图6所示.为掌握新定义的只压不拉(不连续)钢筋本构对塔结构的影响，同时作出钢筋采用原始可受拉(连续)steel02本构时的荷载位移曲线.从图6可以看出，钢筋不连续导致塔结构的承载力下降了5%，塔结构的延性下降了20%.由于钢绞线预压力作用，承载力和延性的折减均在可接受范围内.

表5 用于增量分析的地震动Tab.5 Ground motions used for incremental dynamic analysis

根据各主要截面纤维受力情况及荷载位移曲线特点，同时参考抗震规范层间位移角限值，以高耸结构设计中常用的水平位移角[11](顶部水平位移Δ与结构总高度H之比)为性能指标，提取4个体外预应力混凝土风力发电塔性能点，如表6所示.

图6 pushover分析得到的荷载位移曲线Fig.6 Load-displacement curve obtained from pushover analysis

4.3 IDA

对选取的20条地震动按峰值地面加速度进行调幅，调幅后的峰值地面加速度分别为0.05g，0.10g，…，0.75g，其中调幅梯度为0.05g.采用调幅后获得的300条地震记录逐一进行弹塑性动力时程分析，考虑二阶效应.地震动沿Y轴单向输入.汇总多次分析得到的数据点，并进行插值，得到地震动强度参数(IM)和结构破坏参数之间的关系曲线，即IDA曲线，如图7所示.曲线形状各异，说明结构的破坏机制有所不同，IDA曲线簇较为全面地反映了结构在不同地震强度下可能出现的地震反应.

表6 体外预应力混凝土风力发电塔损伤状态限值Tab.6 Quantitative values of each damage stage

注：层间位移角限值按规范[10]中混凝土框架结构取值.

5 易损性分析

5.1 概率地震需求模型

结构的地震易损性可表达为在给定地震强度参数下，结构地震需求达到或超过其抗震能力的概率，如下所示：

F(y)=Pf[Ls|IM=y]=P[C≤D|IM=y]

(1)

式中：Ls为极限状态;D为结构地震需求;C为结构抗震能力.通常假设D和C是2个独立的随机变量，均服从对数正态分布，故地震易损性或失效概率可写作

(2)

式中：Φ(·)为标准正态分布函数；SD和SC分别为D和C的均值；βD|IM为lnD在指定IM下的标准差；βC为lnC的标准差.

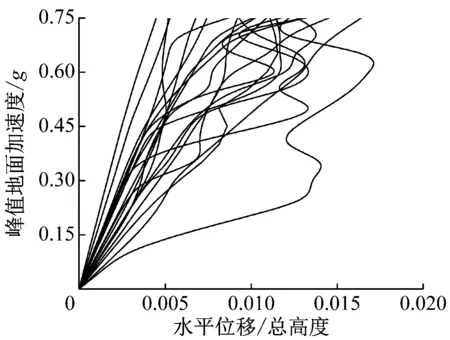
图7 IDA曲线Fig.7 IDA curves

一般假设D与IM近似服从幂指数关系，如下所示：

(3)

对式(3)两边取对数，可得

lnSD=lna+blnIM

(4)

式中：a和b为待定系数.

5.2 概率地震需求分析结果

将得到的300个峰值地面加速度-水平位移角离散数据点在对数空间表示，如图8所示.其中，35次时程分析在运算完成前出现了收敛困难，认为结构发生完全损伤，此时取已完成计算时长中最大的水平位移角为此次时程分析的地震需求.

图8 地震需求参数拟合Fig.8 Regression analysis of seismic demand parameter

采用最小二乘法对300个峰值地面加速度-水平位移角离散数据点进行回归分析，建立水平位移角与峰值地面加速度间的函数关系.概率地震需求模型为

(5)

5.3 体外预应力混凝土风力发电塔易损性曲线

将式(5)代入式(2)可得以IM表示的体外预应力混凝土风力发电塔在不同地震水平下超越某一极限损伤状态的概率函数，如下所示：

(6)

分别将IM=0.05g,0.10g,…,0.75g代入式(6)中，可得各极限状态在各级地震强度下发生的概率，形成易损性曲线，如图9所示.在图9中标记不收敛时程分析频率的散点，与完全损伤的易损性曲线形成对照.

图9 体外预应力混凝土风力发电塔易损性曲线Fig.9 Fragility curves of external prestressed concrete wind tower at all damage states

由图9可知:在7度多遇地震(峰值地面加速度0.035g)下，该混凝土风力发电塔基本处于弹性工作状态，发生各级损伤的概率接近零；在7度基本烈度地震(峰值地面加速度0.100g)下，该混凝土风力发电塔发生轻微损伤的概率为1%，发生中等损伤、严重损伤及完全损伤的概率基本为零；罕遇地震(峰值地面加速度0.220g)下，该混凝土风力发电塔发生轻微损伤、中等损伤、严重损伤及完全损伤的概率分别为40%、20%、1.3%、0.因此,可认为该混凝土风力发电塔满足抗震设防的要求.另外，在8度罕遇地震(峰值地面加速度0.400g)下，混凝土风力发电塔发生轻微损伤、中等损伤、严重损伤及完全损伤的概率分别为89%、74%、25%、5%.因此，在将该预应力混凝土风力发电塔应用于高烈度区时应谨慎计算地震作用和效应.