稀疏求解的动力学显隐混合异步长交错计算方法
2018-12-04马志强孔令爽楼云锋金先龙
马志强 孔令爽 楼云锋 金先龙
(1.上海交通大学机械与动力工程学院, 上海 200240; 2.上海交通大学机械系统与振动国家重点实验室, 上海 200240)
0 引言
直接积分法是求解有限元结构动力学问题的常用方法,可分为显式与隐式两大类。显式方法适合求解冲击载荷引起的波传播问题,隐式方法适合求解结构低频振动问题[1]。复杂结构动力学分析中常涉及不同时间与网格尺度,结合显式与隐式方法优点的显隐混合算法是求解此类问题的经典方法[2]。这类显隐混合方法可以追溯到BELYTSCHKO等[3]的研究。在近40年的研究历程中,大致可以分为2个阶段。早期的研究以显隐同步长为起点,结合显式、隐式在求解动力学问题上的优势处理复杂结构动力学问题[3-5]。国内外学者尝试将显隐混合积分方法运用到分布式发电系统、流固耦合等领域[6-8]。节点分割和单元分割是两种有限元模型的分区方法,显隐分区边界多采用共享节点形式[9-11]。显式方法多采用中心差分法,隐式积分方法常采用Newmark方法。不同的显隐混合方法多集中保证不同分区边界数据连续性上,尤其对显隐异步长而言,显式分区计算时常需要对隐式分区边界节点数据作插值处理[12],这在一定程度上增加了算法对边界数据的连续性要求[13],也降低了显隐最大步长比的选择。
随后,以FETI(Finite element tearing and interconnect method)方法为基础,采用拉格朗日乘子耦合分区边界的GC方法与PH方法被先后提出[14-15]。不同分区异步长插值处理由节点变量(位移、加速度等)变成拉格朗日乘子[16],同样存在上述边界数据连续性问题。作为共享边界节点的一种替换方案,重叠网格形式的Arlequin模型体现了在求解结构动力系问题上的稳定性优势[17]。
本文参考Arlequin结构动力学模型,以重叠网格为基础,提出一种改进的显隐混合异步长计算方法。采用节点分割有限元模型,分区边界节点与外部节点构成耦合区域。
1 结构动力学显式与隐式计算方法
结构经有限元离散,含阻尼的线弹性体结构动力学方程可以写为[1]
(1)
式中M、C、K——结构质量、阻尼与刚度矩阵
fext——节点外力向量

阻尼矩阵C常用Rayleigh阻尼形式。为了统一显式与隐式求解格式,采用基于预测校正格式的Newmark格式。预测校正格式求解过程分为预测步、加速度求解以及校正步3个求解过程。预测步中,第n+1时间步节点速度以及位移的预测值可以由第n时间步节点的位移、速度以及加速度表示为
(2)

β、γ——Newmark时间积分参数
Δt——积分时间步长

(3)

1.1 显式求解格式
显式求解过程是将时间离散后的位移与速度的预测值式(2)直接代入方程(1)中,此时节点加速度求解公式为[1]
(4)
质量矩阵采用集中质量矩阵形式,加速度求解过程无需进行矩阵求逆。
1.2 隐式求解格式
与显式求解格式相兼容的隐式方法是将速度与位移的校正式(3)代入方程(1)中,隐式方法中的加速度求解写成
(5)
其中
Keff=M+γΔtC+βΔt2K
式中Keff——求解节点加速度的等效刚度矩阵
由于刚度矩阵为稀疏非对角矩阵,节点加速度求解过程涉及等效刚度矩阵的求逆过程。式(4)与式(5)为格式兼容的显式与隐式预测校正Newmark加速度求解格式,此格式用于显隐混合求解的优势在于显式与隐式求解可以融合在统一的程序中。
2 交替格式的混合异步长耦合计算方法
交替格式的显隐式适用于多个分区的求解过程,为了方便描述,本节以两个分区为例。有限元网格采用节点分割分成显式与隐式两个分区。与经典的显隐混合计算方法不同,交替格式的方法采用边界重叠多重网格的方法实现异步长显隐边界数据的交换。
2.1 节点划分的重叠网格
隐式分区采用大时间步长Δt1,显式分区采用较小的子循环步长Δt2。假定隐式分区步长是显式分区步长的整数m倍,即Δt1=mΔt2。图1是以2倍步长比为例的重叠网格分区示意图。隐式与显式分区均包含内部节点、边界节点与外部节点,其中边界节点与外部节点构成重合区域。一个完整的系统时间步包含一个隐式时间步和多个显式子循环时间步。内部节点、边界节点与外部节点用符号I、B、E表示。隐式分区的边界节点即为显式分区的外部节点,显式分区的边界节点为隐式分区的外部节点。

图1 多重边界网格显隐分区示意图Fig.1 Explicit-implicit partitioned schematics with multiple boundary mesh
2.2 显式小步长分区计算
显式计算过程中,求解某节点下一时刻数据只与当前时刻该节点的相邻节点信息有关。在显式子循环过程中,可正确求得的外部节点数据逐层递减。子循环结束后显式分区内部与边界节点数据可以正确求出。边界节点加速度求解公式可以写成
(6)
式中MB——与边界节点相对应的质量矩阵


m——隐式分区与显式分区的步长比
2.3 隐式大步长分区计算
隐式分区的节点加速度求解公式可以写成
(7)
式中KE——隐式分区等效刚度矩阵Keff按照外部节点的分块矩阵
KE(B+I)、K(B+I)E——隐式分区等效刚度矩阵Keff按照边界节点的分块矩阵
KB+I——等效刚度矩阵Keff与内部节点对应的分块矩阵

对于隐式分区而言,隐式内部与边界节点加速度求解是域分解方法中回代求解过程[18]
(8)
采用稀疏直接求解器计算出隐式分区内部节点与边界节点加速度,赋值给显式分区外部节点,完成一个系统时间步的显式与隐式分区节点数据的求解。交替格式的混合异步长耦合计算方法求解顺序为显式子循环时间步、隐式分区回代求解以及显式分区外部节点赋值3个串行交替步骤。显隐异步长串行交替求解流程如图2所示。虚线框内是显式分区节点与隐式分区节点加速度数据赋值过程。

图2 显隐异步长串行交替求解流程Fig.2 Sequential format process for explicit-implicit mixed multi-time step
2.4 隐式分区的稀疏行压缩存储格式的实现
显式分区求解中质量矩阵为对角矩阵,节点加速度直接根据节点自由度编号形成方程。方程(4)右端载荷项也是在单元层级计算按照节点自由度累加形成。采用坐标存储对应节点自由度质量项与载荷项即可。
而对于隐式分区而言等效刚度矩阵为稀疏对称矩阵,求解内部与边界节点加速度过程涉及矩阵求逆。采用稀疏矩阵的行压缩CRS存储格式有较好的存储和求解效率[19]。隐式分区节点按照先外部节点后边界与内部节点的顺序编号,将分区等效刚度矩阵与右端载荷项分块。

3 精度验证
采用弹簧质量系统验证算法的计算精度与收敛性。5节点弹簧质量系统如图3所示。采用的弹簧质量参数为ki=1 N/m(i=1,2,…,6),mj=50 kg(j=1,2,…,5)。初始位移条件为u0=(0,0,1,0,0),各个节点初始速度均为0。显式与隐式分区参数均为β=0.5,γ=0.25。分区同步长计算时节点3、4与弹簧k4为重叠区域。为了比较显隐分区步长比对精度的影响,异步长计算时选择步长比m=3。此时节点2~5,弹簧3~5为重叠区域,节点m1为显式分区内部节点。集中参数的弹簧质量系统的解析解作为计算结果的参考对象。图中ui表示第i个节点的位移。

图3 5节点弹簧质量系统Fig.3 Five-node spring mass system
显式分区时间步长为0.001 s,分别采用显隐同步长、3倍步长比以及GC 3倍步长比方法[14]计算节点3的位移与理论计算结果相比较。图4为使用不同方法的位移计算结果。其中图4a为节点3位移计算结果,因为节点5弹簧质量系统初始条件为节点3的位移,节点2与节点4的理论位移应该重叠,u2-u4可以直观地反映不同方法下的位移计算误差,如图4b所示。
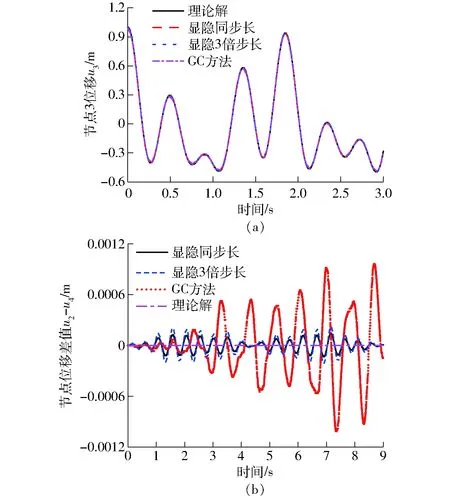
图4 不同方法弹簧质量系统位移节点结果Fig.4 Nodal displacement results of spring mass system with different methods
从图4a可以看出,3种方法均可以计算出弹簧质量系统的节点位移。由图4b可知,显式分区采用相同步长,隐式分区由同步长到3倍步长条件下,位移误差有所增加,但是误差在一个有限的区间内波动。GC方法在计算节点位移时,涉及拉格朗日乘子处理,同时随着仿真时间步的进行,位移误差逐步增大。相同步长比条件下,本文所述方法具有较高的求解精度。
位移收敛特性采用相对位移计算结果[20]
(9)
式中ui——i时刻5个节点位移向量

统计显式分区步长从0.001、0.002、0.006、0.01 s的位移误差曲线,采用双对数坐标系,统计时间为9 s,n取900,结果如图5所示。
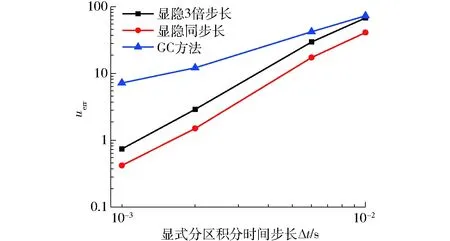
图5 位移误差收敛曲线Fig.5 Displacement error convergence rate curves for different methods
计算曲线结果表明,在显隐分区积分参数均为β=0.5,γ=0.25的条件下,显隐混合异步长计算方法具有2阶的位移收敛精度。同显式分区步长条件下,步长比m越大所得的计算误差越大。
4 数值算例
为了进一步验证算法在精度和效率方面的特性,本节采用U型管承受局部冲击载荷fext作为数值算例。图6为结构有限元模型与外载荷时间历程曲线。
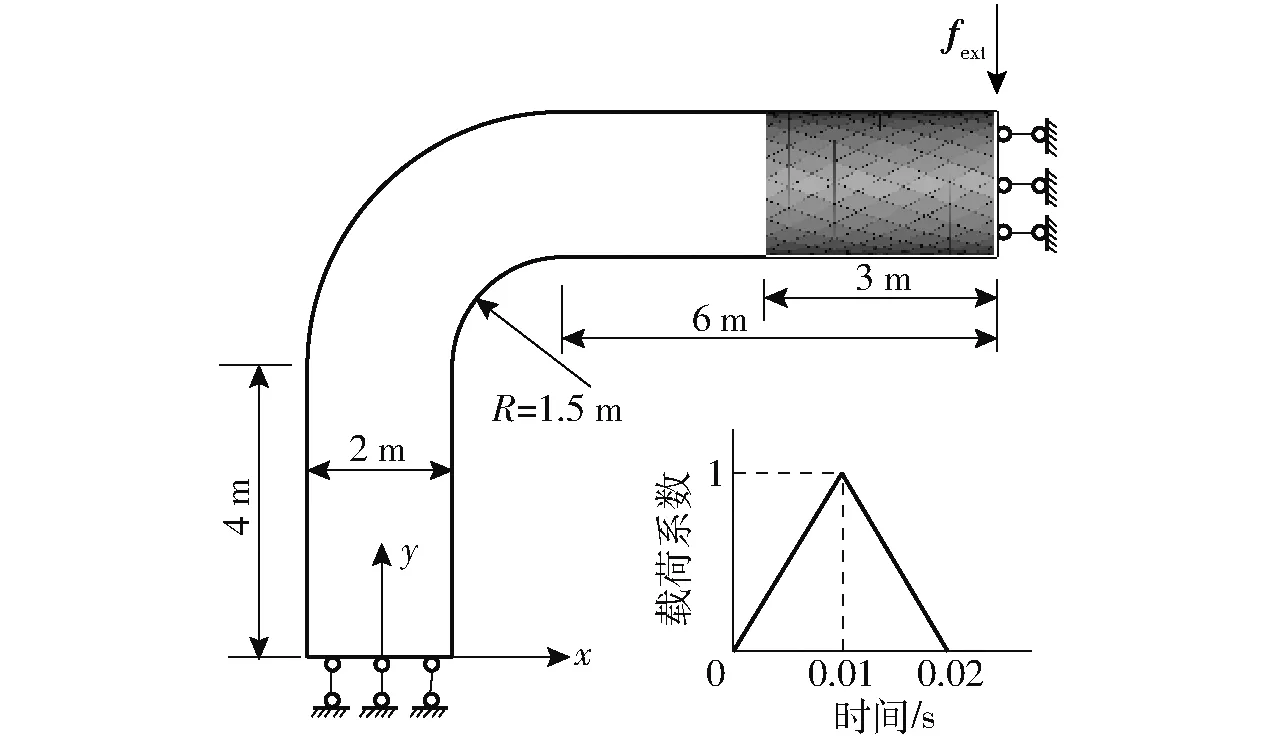
图6 U型管有限元模型及载荷时间曲线Fig.6 Finite element model and load time curve for U-type tube
模型左右对称,计算时采用整体模型的一半。采用各向同性材料,材料弹性模型E为210 GPa,材料密度ρ为7 800 kg/m3,泊松比υ为0.28。U型管半径为1 m,管壁厚度为8 mm。管中间部位承受弯曲载荷fext,载荷最大为1.5×105N。结构采用三角形壳单元离散,冲击部位与管弯曲部分网格尺度较小。显式计算部分如图6中所画网格部位,重叠部分单元为管壁若干圈单元。模型含有13 574个节点,26 992个单元。
采用显式积分方法时受限于稳定性条件,采用积分时间步长Δt=2×10-6s。仿真时间0.1 s。隐式分区分别采用时间积分步长为mΔt。图7为在步长比m为3、12这两种情况下冲击点竖向位移曲线。参考曲线为商业软件LS-DYNA显式计算结果。从图7可以看出,随着步长比的增加,算法计算结果符合位移计算规律,精度稳定性较好。

图7 不同方法计算节点竖向位移结果Fig.7 Vertical displacement results for impact node by different methods
为了研究算法计算效率,将本文方法与经典显式中心差分方法用于U型管的冲击计算。模型在共享内存模式计算机上计算,CPU主频4.2 GHz,内存16 GB。统计的有限元模型计算时间见表1。表中m表示隐式分区积分时间步长是显式分区的倍数。
从表1可以看出,随着步长比的增加,模型求解时间得以降低。由于采用串行计算格式,一个系统时间步内显式分区先计算,隐式分区后计算,提高显隐分区步长比意味着在显式分区步长不变的情况下,隐式分区采用了更大的时间步长。考虑重叠单元的边界处理,在不同步长比下,隐式分区单元保持一致,显式分区单元规模需增加部分分区边界单元。计算时间的减少主要来自隐式分区计算步数的降低。也需要看到随着显隐步长比增加,时间比率减少幅度减少,此时隐式分区计算时间减少有限,计算时间占比中显式计算所占比重逐渐增大。

表1 显隐分区不同步长比计算时间Tab.1 Computational times for proposed explicit-implicit method with different time step ratios
5 结论
(1)分区边界数据传递不涉及插值过程,这一改进提高了计算精度,积分参数β=0.5,γ=0.25,方法具有二阶收敛精度。
(2)显隐分区根据单元属性选择时间积分步长,降低计算时间。一定程度上,步长比越大,计算所需时间越小。
(3)显隐分区采用兼容的Newmark格式,基于稀疏存储CRS格式,显隐计算程序可以具有统一的计算格式,这为显隐式混合积分扩展至并行化提供了便利。
