翼型最大拱度位置对轴流泵水力性能影响的模拟与试验

2018-12-04石丽建付玲玲汤方平孙丹丹翟林鹏

农业机械学报 2018年11期

石丽建付玲玲夏烨汤方平孙丹丹翟林鹏

(1.扬州大学水利与能源动力工程学院，扬州 225127； 2.扬州大学广陵学院，扬州 225000；3.徐州市水利建筑设计研究院，徐州 221002； 4.江苏省农村水利科技发展中心，南京 210029)

0 引言

轴流泵站中最核心的部件是叶轮，轴流泵叶轮设计的好坏直接关乎泵站的运行状况。而翼型拱度是轴流泵较多设计参数中最为关键的设计参数之一。因此，研究翼型拱度对轴流泵水力性能的影响非常有必要。

目前在轴流泵设计领域，除关醒凡[1]提出了适合于轴流泵设计的791翼型，未见其他关于轴流泵翼型的应用报道。但在风力机领域关于翼型研究的报道较多[2-13]。在轴流泵设计方面，LI[14]针对轴流泵的空化性能借助响应面方法进行了优化设计。LIU[15]兼顾对流动分离的控制对轴流泵进行优化设计，提高了机组的空化性能。严敬等[16]将奇点分布法应用于轴流泵叶轮叶片设计。杨敬江等[17]、汤方平等[18]、毛秀丽等[19]均在流体机械设计理论方法做了相关研究。

根据国内外研究现状可知，在风力机、航空航天领域关于翼型设计、翼型优化研究较多，而轴流泵设计过程中大多直接采用美国航天局研制的NACA翼型，关于轴流泵翼型研究较少，特别是关于翼型拱度对轴流泵水力性能的影响研究未见报道。本文从二维翼型角度出发，改变NACA翼型拱度大小及位置，其他设计参数保持不变，采用平面叶栅理论设计轴流泵叶轮，在试验数据基础上，分析翼型拱度对轴流泵水力性能的影响。

1 翼型数值计算与优化

1.1 翼型几何参数

流体机械叶片的截面形状称为翼型。翼型的形状一般都是圆头尖尾的流线形。翼型的各部分名称及相关几何参数(图1)定义如下[20]。

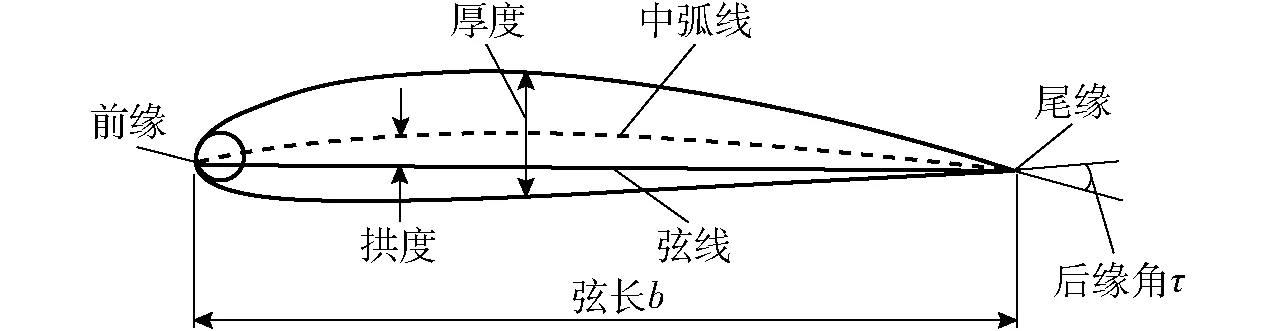
图1 翼型几何参数Fig.1 Airfoil geometry parameters

前缘：翼型上最前端。

尾缘：翼型上最后端。

前缘半径：构成翼型前缘区域的圆弧的半径。

弦线：前缘与后缘的连线，是翼型的基准线。

厚度：上弧线同下弧线之间内切圆的直径，也是翼型上下表面之间的距离。

中弧线：上弧线和下弧线之间的内切圆圆心的连线，即厚度中点的连线。

拱度：垂直于弦线，介于中弧线和弦线间的线段，其中最长的线段叫最大拱度。

1.2 翼型动力特性

实际液体绕翼型流动时，绕流液体和翼型之间会产生力的作用。可以将力分解为相互垂直的两个力：一个为垂直于来流方向的力Py，称为升力，另一个为平行于来流方向的力Px，称为阻力。其作用力分解如图2所示。

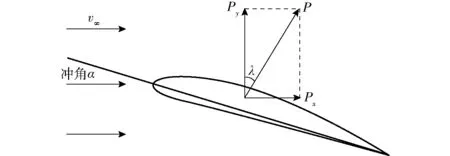
图2 绕流液体对翼型作用力Fig.2 Airfoil force diagram

升力Py和阻力Px计算公式为

(1)

(2)

式中Cl、Cd——翼型的升力和阻力系数

A——翼型的最大投影面积

v∞——无穷远来流速度

ρ——水的密度

Cl、Cd的大小与翼型的几何参数、雷诺数及翼型的冲角有关，一般其数值可由风洞试验确定。升力系数Cl与阻力系数Cd的比值称为升阻比,该值较大的区域称为翼型工作高质量区。在设计翼型时，为提高效率通常希望翼型的升阻比处于翼型工作高质量区，即合力与升力的夹角λ越小，升力越大，阻力越小，翼型质量越好。

1.3 翼型数值计算

1.3.1网格无关性分析

本文采用ICEM对翼型进行结构化网格划分。通过对翼型边界层网格加密，划分不同的网格数量，对NACA66翼型进行网格无关性分析，网格数从20万到80万共计分析4个方案，升阻比随着网格数增加而增大，当网格数达到60万左右时，升阻比趋于稳定。计算网格如图3所示。根据无关性分析结果，本文最终网格数量选择613 584。不同方案网格数量相当。

图3 计算网格模型Fig.3 Grid computing model

1.3.2翼型计算模型

为使进出水断面流态一致，采用矩形计算区域。为使来流充分发展，翼型上游长度取5倍弦长，下游长度取10倍弦长，宽度方向取10倍弦长。

轴流泵的叶轮直径为300 mm，额定转速为1 450 r/min。叶轮在半径为r处的流体速度为

(3)

式中ω——叶轮旋转角速度，rad/s

n——水泵转速，r/min

通过计算，翼型无穷远来流速度设为20 m/s。数值计算采用时均的N-S方程，紊流模型为RNGk-ε模型。进口边界条件设置为速度进口条件。出口边界条件设置为压力出口条件。壁面边界条件设置为无滑移条件，其他边界设置为对称边界symmetry条件。

1.4 翼型优化

本文研究最大翼型拱度位置对轴流泵水力性能的影响。而根据轴流泵设计采用NACA的基础翼型，最大翼型拱度位置是固定的，从翼型前缘到翼型尾缘拱度分布规律也是给定的。当改变最大翼型拱度位置时，翼型的拱度分布无法给定，即使能得到翼型拱度的分布规律，此时翼型的升力系数和升阻比均发生了变化。继续进行轴流泵叶轮设计时，叶轮的设计工况会发生变化，设计工况改变后无法比较拱度变化对轴流泵性能的影响规律。因此，需对翼型进行优化，保证最大拱度位置发生变化时，寻求较好的拱度分布规律，使翼型的升力系数基本不变，进而使得设计得到的轴流泵叶轮同样的设计流量下设计扬程基本保持不变。

对于翼型的优化方式，本文主要研究在保证升力系数基本一致的情况下，仅改变翼型的中弧线分布规律，即改变最大拱度的位置及大小，在新的中弧线上加载相同厚度，对比分析新形成的翼型的升、阻力系数、翼型表面压力分布等特性。

其具体优化方法如下：

(1)通过Matlab编写应用程序，采用Bezier曲线控制翼型中弧线的分布规律，Bezier曲线采用四阶曲线，第1和第5个控制点固定不动，改变其余3个控制点以改变中弧线分布。最大拱度位置分别设置在0.3L～0.65L，间隔长度0.05L，L为弦长，研究8个不同最大拱度位置的翼型性能。

(2)最大拱度位置固定后，以翼型的升力系数为目标。只改变控制点的纵坐标，寻找到升力系数与参考翼型升力系数相同的控制点，由此，确定新翼型的拱度分布规律。

(3)根据Bezier曲线通过程序得到新翼型的中弧线分布规律，与原始翼型保持相同厚度比，并加载相同的厚度分布规律，形成新翼型，计算比较新翼型与初始翼型的升力系数。考虑到升力系数计算值不完全一样，其误差在2%以内则认为寻找到目标翼型；若误差大于2%，回到步骤(2)，继续寻找。

最大拱度处于不同位置时的升、阻力系数及升阻比如表1所示。其中升力系数的误差为各翼型计算的升力与初始翼型升力的差值占初始翼型升力的比值。

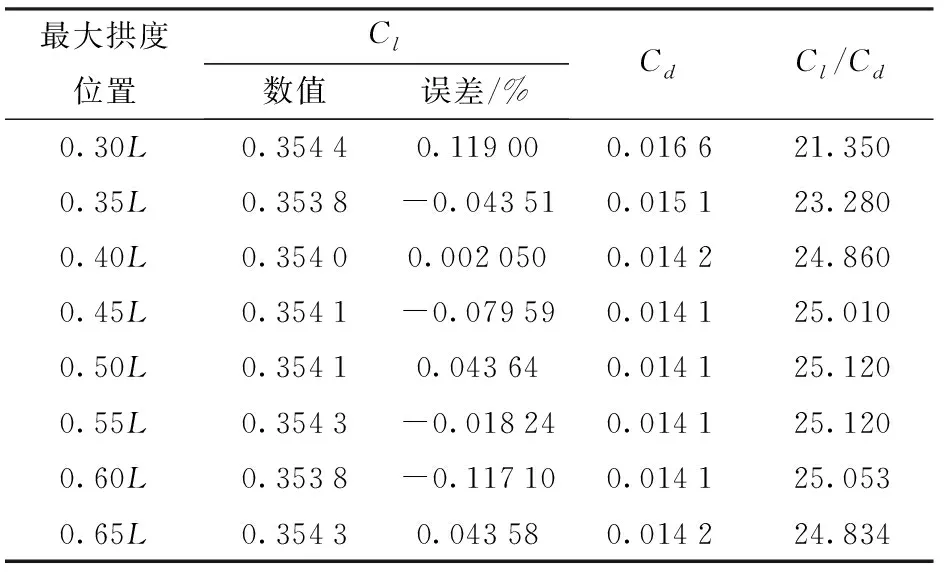
表1 不同最大拱度位置翼型参数Tab.1 Different airfoil design parameters

从表1可看出，升力系数的误差比较小，均不超过2%，可认为翼型的升力系数是一致的。根据升阻比计算结果可知，在优化得到的翼型中，最大拱度位置偏大或者偏小时，翼型的升阻比减小，带来的影响是翼型的阻力增大，翼型设计质量偏低。因此，在轴流泵设计过程中翼型最大拱度位置不宜选择过小或过大，翼型最大拱度位置的选择应在0.4L～0.6L之间。

最大拱度位置不同的翼型表面压力分布如图4所示。

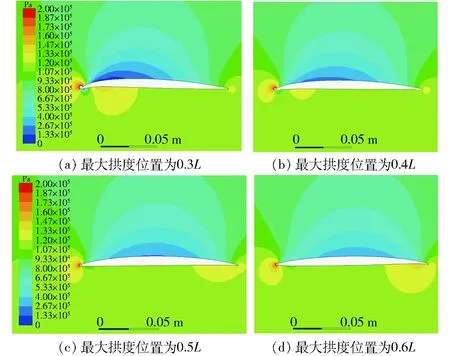
图4 不同优化翼型压力分布图Fig.4 Pressure distribution maps of different optimized airfoils

最大拱度位置不同时吸力面的整体变化规律基本相同。随着最大拱度位置向尾缘偏移，翼型背面局部低压区会朝着翼型尾缘移动，最小压力值有所增大。说明翼型背面低压区分布规律与最大翼型拱度密切相关，这也反映在轴流泵叶轮汽蚀性能上。当最大拱度位置靠近翼型前缘时，翼型前缘高压区范围较大，随着最大拱度位置向翼型尾缘移动，高压区范围缩小。这是因为当最大拱度位置靠进前缘时，翼型前缘位置拱度增加，进流冲击较大，固壁附近速度降低，压力增加。当翼型靠近尾缘时，翼型尾部会产生高压区，这是因为最大拱度处于翼型尾部导致翼型尾缘曲率增大。

2 轴流泵叶轮设计与性能分析

2.1 轴流泵设计

考虑到轴流泵叶片负荷小，在设计工况下径向分速度较小，本文采用径向平衡方程来进行通流计算，再根据平面叶栅理论，通过面元法求解来完成叶栅造型，从而实现既稳定快速又有一定精度的轴流泵叶轮设计。在轴流泵叶轮设计过程中，将叶片沿径向分成若干展开的圆周面，展开后即为不同翼型断面。本文将轴流泵叶轮从轮毂到轮缘分成11个翼型断面，翼型的半径为50、60、70、80、90、100、110、120、130、140、150 mm。轴流泵叶轮设计涉及到11个断面的设计参数，包括翼型安放角、叶栅稠密度、最大拱度比(拱度长度与弦长的比值)和最大厚度比等。选取最大翼型拱度位置分别为0.4L、0.5L和0.6L的翼型共计3种方案，即采用上述对应的二维翼型优化结果作为3副轴流泵叶轮的基础翼型。3副轴流泵叶轮除了翼型拱度不一样外其他设计参数均保持一致。以某一比转数轴流泵叶轮为例，其11个断面的主要设计参数如表2所示。

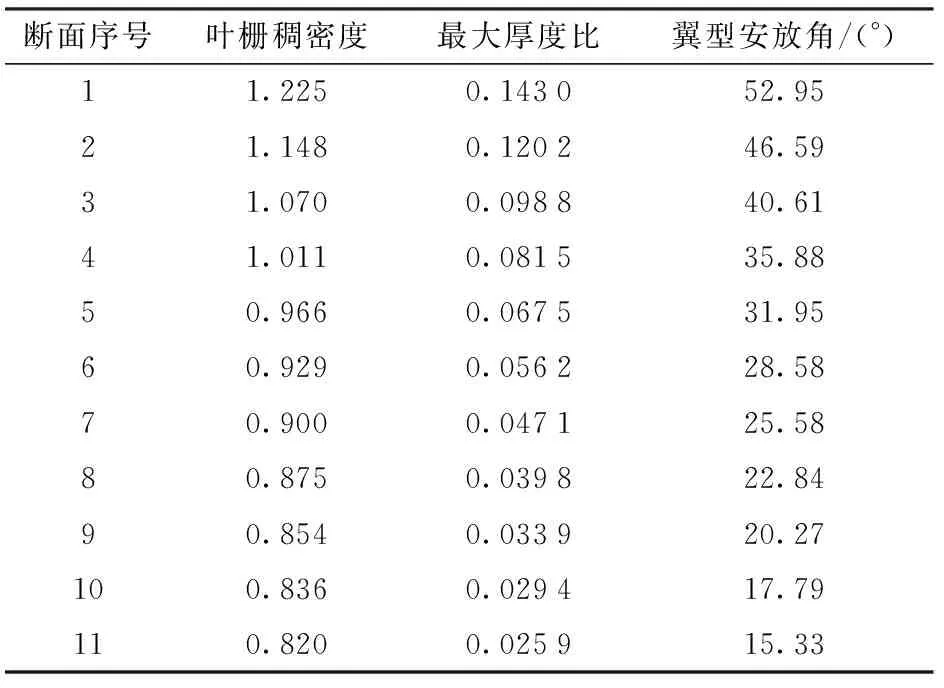
表2 轴流泵各断面主要设计参数Tab.2 Each section design parameters of axial-flow pump

根据优化得到的二维翼型，计算最大拱度位置为0.4L、0.5L和0.6L共3种翼型的升力系数与最大拱度比之间的关系。具体计算保证每种翼型的拱度分布规律不变，只改变最大翼型拱度比，得到最大翼型拱度比与升力系数曲线。最后根据初始叶轮11个断面的翼型的升力系数，从曲线中找出对应的最大翼型拱度比，即为叶轮不同断面的最大翼型拱度比。不同拱度位置的翼型如图5所示。

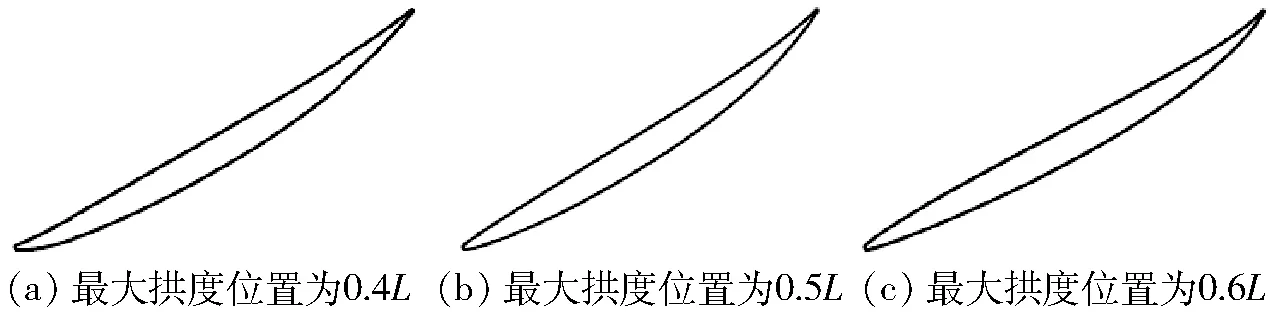
图5 不同拱度位置的中间断面翼型Fig.5 Intermediate section airfoil with different camber positions

2.2 轴流泵CFD计算

采用ANSYS-CFX对叶轮内部三维不可压缩紊流流场进行数值模拟，计算流场外特性参数，为了快速准确地了解设计叶轮的性能，本文CFD计算的计算域包括进水直管、叶轮、配套导叶和60°出水弯管。叶轮叶片安放角为0°，叶片数为4片，导叶叶片数7片，叶顶间隙为0.15 mm，转速为1 450 r/min。叶轮与导叶的模型在TurboGird软件中建模，进水管及出水弯管均在ICEM软件中建模。计算模型如图6所示。叶轮模型示意图如图7所示。

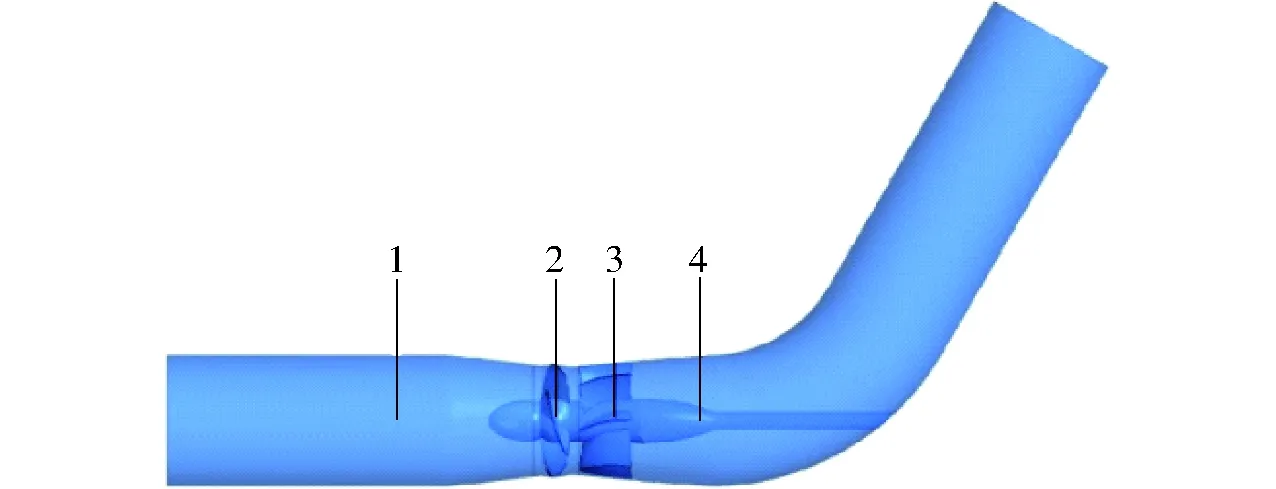
图6 计算区域图Fig.6 Calculation model diagram1.进水直管 2.叶轮 3.导叶 4.出水弯管

图7 叶轮三维造型图Fig.7 Three-dimensional model of impeller

采用定常计算方式进行外特性预测，采用SST紊流模型与雷诺时均N-S方程，收敛精度设置为10-5。流量计算工况为300、330、350、360、370、390 L/s。进口边界条件设置为总压进口条件，总压设置为101.325 kPa。出口边界条件设置为质量流量出口。壁面边界条件设置包括叶片表面、轮毂表面、轮缘和管道内表面等。表面固壁上满足粘性流体的无滑移条件，因此在近壁区域采用标准壁面函数边界条件。导叶和叶轮之间的动静交界面采用速度平均的Stage交界面模型，其余交界面均使用None模型。

2.3 计算结果分析

基于能量方程计算泵装置扬程，由计算得到的速度场和压力场以及叶轮上作用的扭矩预测泵装置的水力性能。泵装置进水管进口处与出水弯管出口处的总能量差值设定为装置的扬程，计算公式为

(4)

式中Q——流量,L/s

H1、H2——泵装置进、出水断面高程，m

S1、S2——泵装置进、出水断面面积，m2

u1、u2——泵装置进、出水流道断面各点流速，m/s

ut——水流圆周速度，m/s

ut1、ut2——泵装置进、出水流道断面各点流速法向分量，m/s

P1、P2——泵装置进、出水断面各点静压，Pa

泵段效率计算公式为

(5)

式中Tp——扭矩，N·m

将 3 副不同拱度的轴流泵水力模型组合成泵段进行水力性能计算，分别命名为A泵段(最大拱度位置0.4L)、B泵段(最大拱度位置0.5L)和C泵段(最大拱度位置0.6L)。3副叶轮对应的泵段能量性能计算结果如图8所示。

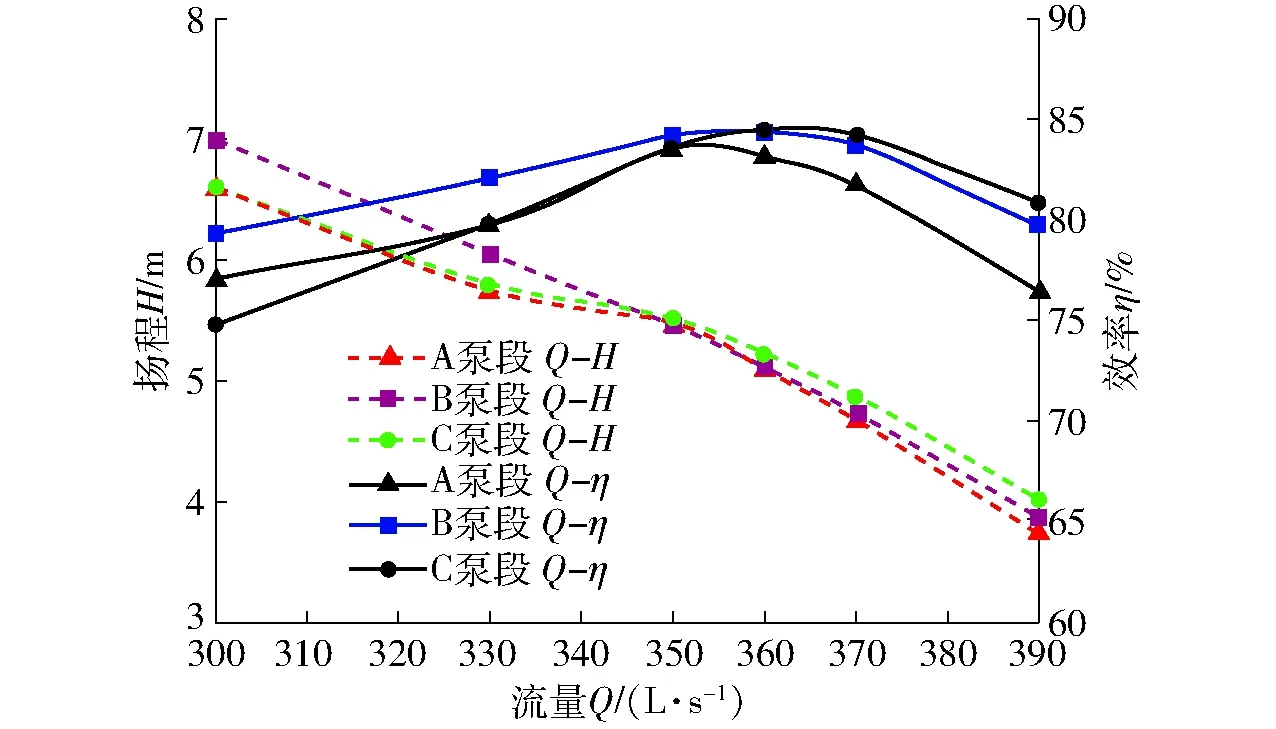
图8 不同泵段外特性数值计算结果对比Fig.8 Comparison of numerical calculation results of different pump sections

根据图8可知，不同水力模型的泵段效率和扬程的总体变化趋势一致。从流量扬程曲线上看，最大拱度位置为0.5L时，流量扬程曲线较为平顺。在大流量区域，最大拱度位置越靠近翼型尾缘，做功能力越大，扬程越高。从流量效率曲线上看，B泵段对应的高效区范围更宽。在设计工况时，B泵段的效率较高，达到84.31%。在小流量区域，B泵段的效率均大于A泵段和C泵段，且随着流量的进一步减小，B泵段的效率优势更为明显，说明对于小流量工况而言，翼型最大拱度位置处在翼型正中间会取得最优的效果。在大流量区域，C泵段效率为3个泵段中最大，其次是B泵段，最后是A泵段，即翼型最大拱度位置越向翼型尾缘移动，其泵段大流量区域效率越高。对于常年运行在大流量工况的泵站而言，选用最大翼型拱度位置靠近尾缘的翼型有较好的效果。因此，翼型拱度的选择对轴流泵水力模型能量性能影响较大，总体而言，翼型最大拱度位置在0.5L时，具有较好的水力性能。对于大流量运行较多的泵站，在针对性设计时可适当将最大拱度位置向翼型尾缘偏移。

将叶片展向90%位置断面(span值为0.9)的压力分布取出，用以分析比较其汽蚀性能，如图9所示。

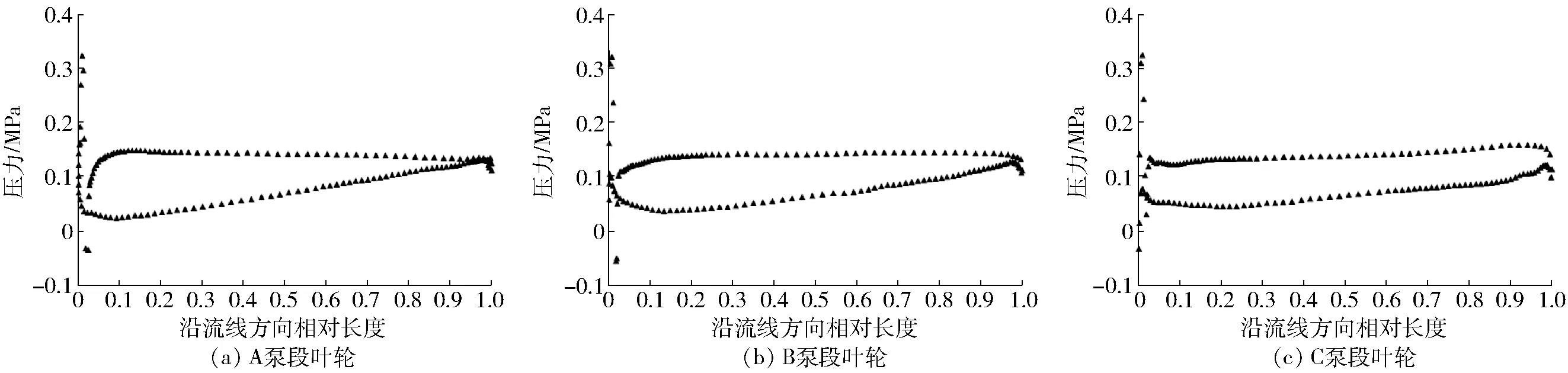
图9 设计工况下span值为0.9位置压力分布Fig.9 Pressure distribution diagram with span of 0.9 under design condition

根据文献[21]，可通过叶片背面沿叶片展向90%的断面且距离叶片进口15%～20%弦长位置的最小压力来预测水泵的汽蚀性能。根据图9可知，A泵段叶轮预测汽蚀位置的压力较小，说明最大翼型拱度靠近前缘时更容易发生汽蚀，对应叶轮的汽蚀性能较差。C泵段叶轮该位置压力较大，对应的必需汽蚀余量较小，汽蚀性能较好，这说明随着最大拱度位置向翼型尾缘的偏移，水泵的汽蚀性能会有一定的提高。

3 模型试验验证

3.1 泵段试验系统

根据泵段数值模拟结果，将B方案叶轮加工后在扬州大学测试中心的高精度水力机械试验台上进行泵段能量性能试验和汽蚀性能试验。模型泵叶轮直径300 mm。叶轮如图10a所示，用黄铜材料经数控加工成型。导叶为配套导叶，用钢质材料焊接成型。模型泵段进出口直径350 mm，带60°标准弯管，叶轮室开有观察窗，便于观测叶片处的水流形态。

图10 叶轮和泵段实物图Fig.10 Model of impeller and pump device

3.2 测试方法

泵段模型试验测试参照GB/T 18149—2000《离心泵、混流泵和轴流泵水力性能试验规范(精密级)》和SL 140—2006《水泵模型及装置模型验收试验规程》执行。

3.3 模型泵段试验结果及分析

模型泵段试验测试了6个叶片安放角(-4°、-2°、0°、2°、4°、6°)的能量性能和汽蚀性能。将0°时的试验结果与数值模拟结果进行对比，如图11所示。并根据试验结果绘出B泵段叶轮水力模型综合特性曲线，如图12所示。

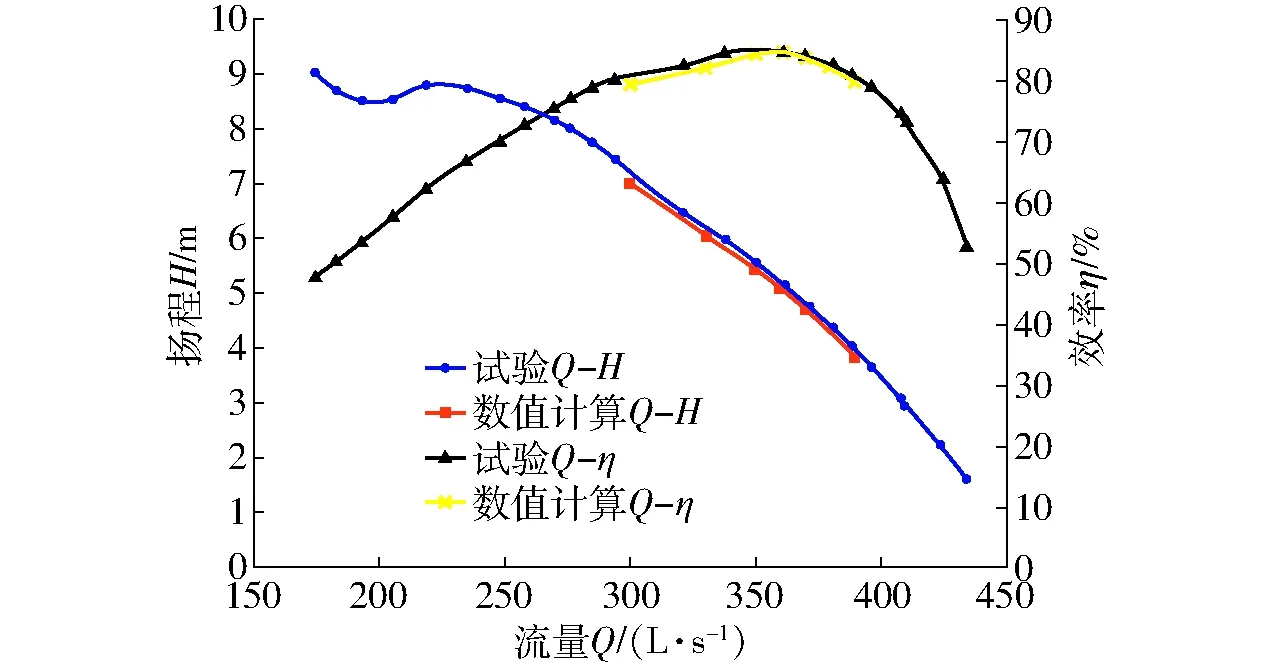
图11 试验结果与数值模拟结果对比Fig.11 Comparison of simulation results and experiment results

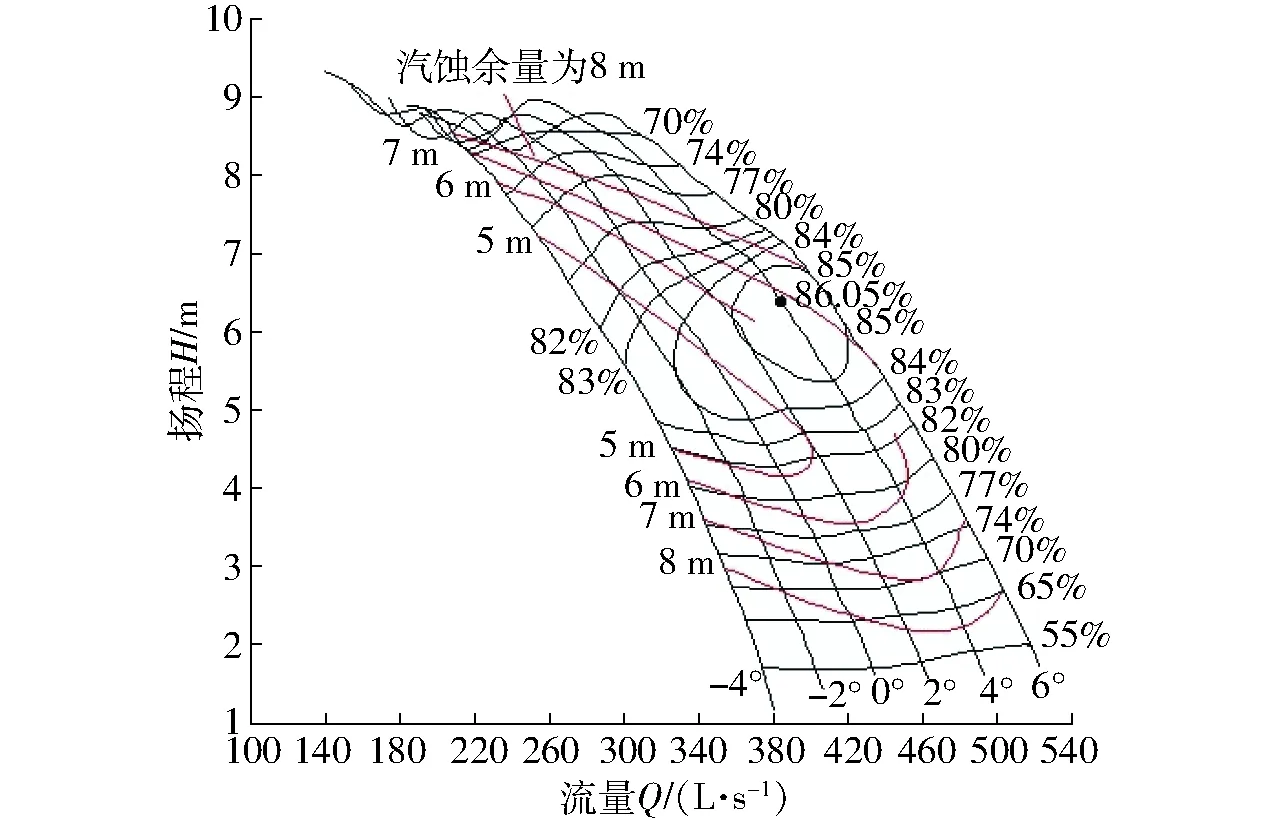
图12 水泵水力模型综合特性曲线Fig.12 Hydraulic model synthetic characteristic curves

根据图11可知，B泵段的数值模拟结果与试验结果误差较小，流量扬程曲线和流量效率曲线基本重合，只在小流量区域数值计算结果有些误差，但均未超过2%。说明水力模型的泵段数值模拟结果是可靠的，数值模拟结果与试验结果得到了相互验证。同时也说明了针对本文翼型拱度的研究结果是准确、可靠的。根据图12水力模型的综合特性曲线可知，本文B泵段的最高效率出现在叶片安放角4°、流量382 L/s、扬程6.487 m时，最高效率为86.05%，临界汽蚀余量7 m，汽蚀比转数1 170。叶片安放角0°时，最高效率84.6%，水泵水力模型的能量和汽蚀性能比较均衡，效率高、临界汽蚀余量小。