螺旋轴式移箱机构多学科协同优化与试验
2018-12-04储婷婷朱德泉
储婷婷,朱德泉,朱 宏,张 顺,蒋 锐,张 俊
(安徽农业大学工学院,安徽合肥230036)
螺旋轴式移箱机构是高速水稻插秧机的关键部件,通过螺旋轴与转子和滑套之间的相互配合,将螺旋轴的旋转运动转化成滑套轴向的左右往复移动,完成高速水稻插秧机的横向送秧工作,其性能直接影响秧苗取秧质量。移箱机构的参数优化是一个多目标、强耦合、非线性问题,涉及到运动学、动力学、结构力学等多个学科。传统的串行优化设计方法,忽略了各学科之间的相互作用和相互影响,设计周期长且只能获得局部最优解,难以满足机械总体设计要求[1-5]。多学科设计优化(multidisciplinary design optimization,MDO)方法充分考虑多个学科及它们之间的耦合关系,利用各学科间的协调作用使得系统整体性能最优,已在船舶、航天飞行器、汽车、电子设计等领域得到了广泛应用[6-17]。
协同优化(collaborative optimization,CO)方法在多学科设计优化中可以消除大量的系统分析,所有学科能够并行地进行分析与优化[10,18-20]。因此,将协同优化方法应用于螺旋轴式移箱机构的多学科设计优化中,建立了螺旋轴式移箱机构分插机构的多学科模型,以运动学、动力学和结构力学等性能为目标函数,采用协同优化方法进行优化计算,学科级优化器采用序列二次规划法优化,构建运动学、动力学和结构力学等学科模型的代理模型,利用iSIGHT软件搭建集成优化平台,对移箱机构进行多学科协同优化近似求解,实现设计参数的最佳组合和产品总体性能最优。
1 螺旋轴式移箱机构结构与工作原理
螺旋轴式移箱机构由螺旋轴、转子、滑块组成,简称双螺旋轴组件,如图1所示。螺旋轴采用双螺旋线和两端的平滑过渡曲线组成,其中过渡曲线的展开线为正弦曲线,如图2所示,转子和滑块结构如图3和图4所示。螺旋轴、转子、滑块主要几何参数取值如表1所示。
工作时,动力传递给螺旋轴使螺旋轴做旋转运动,转子与滑套配合沿着螺旋轴上的双螺旋线做水平运动,在运动到螺旋轴两端过渡曲线螺旋沟槽时,会受到反向旋转力矩,带动滑套转动一定角度,从而实现往复运动,完成高速水稻插秧机的横向送秧工作。

图1 移箱机构结构示意图Fig.1 Structural schematic of moving-box mechanism

图2 螺旋轴外径展开示意图Fig.2 Stretch out view of outer diameter of screw axis
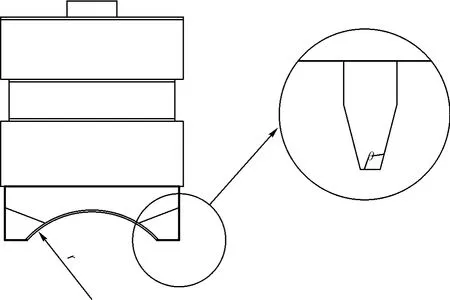
图3 转子结构示意图Fig.3 Stretch of rotor

图4 滑套结构示意图Fig.4 Stretch of sliding sleeve

表1 螺旋轴移箱机构结构参数Table 1 Geometry parameters of moving-box mechanism
2 螺旋式移箱机构学科分析
2.1 动力学性能分析
综合考虑实际螺旋轴工况及为了研究方便,将螺旋轴极限化看成两端固定,可看成一个质量均匀的近似细弦结构。假设螺旋轴单位长度质量为ρ(x),在轴向作用力f(x,t)作用下做轴向的振动,张紧力为 T(x,t),轴向位移函数为 y=y(x,t),由牛顿定律可得:整理可得:


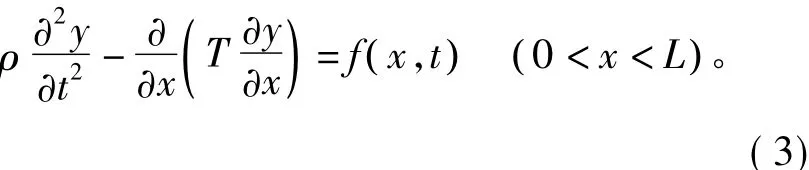
由于螺旋轴两端固定,则

将ρ(x)看作常值ρ,张力T也看作常数,轴向位移y(x,t)较小忽略不计,则式(2)简化为:

则自由振动微分方程为

将边界问题改写成振型位移和振动规律的乘积形式:

将式(7)整理为
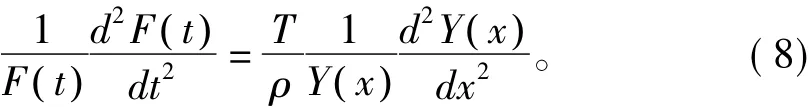
某一时刻t和x相当于一个常数,令为-ω2,由式(8)可得:

则

根据分离变量法,得到t和x的二阶微分方程,故式(9)解得:

设Y(x)的解为

同理,由边界条件y(0,t)和y(L,t)可得E=0,DsinβL=0。
螺旋轴的特征方程为

螺旋轴的固有频率为

在结构的振动过程中,对结构的影响起主要作用的是较低阶的固有频率及其所对应的振型,利用振动微分分析方法对螺旋轴进行模态分析。为了分析螺旋轴的模态,因此不附加任何约束和力,定义单元类型为Solid187,螺旋轴所用的材料为40Cr,采用子空间法模态的提取方法,再扩展模态,完成螺旋轴模态分析模型的建立,提取前8阶模态和频率,如表2所示。
根据表2可知,螺旋轴的前8阶模态随着阶数上升,其频率也随之增加,当螺旋轴转速ωn达到最高时,激振频率为fn=ωn/60≈11.08 Hz。为了保证螺旋轴的平稳安全运行,需要尽可能地偏离激振频率。因此,动力学性能优化的目标是提高一阶固有频率,提升螺旋轴的抗振性能,延长螺旋轴使用寿命。
2.2 运动学性能分析
高速水稻插秧机螺旋轴移箱机构工作时,转子与滑套起着承上启下的作用,主要是将力和运动从螺旋轴传递给秧箱,完成高速水稻插秧机的横向送秧工作。因此,转子与滑套作为移箱机构中受力最复杂的部件之一,为了能在Adams软件中较真实的模拟实际移箱过程中运动性能,首先需对其进行准确和全面的受力分析。螺旋轴中间部分示意图如图5所示。
螺旋轴正常移动部分如图5所示,设螺距为P,则螺旋参数b为:


表2 螺旋轴模态分析结果Table 2 Modal analysis results of screw axis

图5 螺旋轴中间部分示意图Fig.5 Stretch out view of screw axis on middle part
设螺旋回转角为φ,时间为t,则转子移动距离为bφ,于是得到螺旋轴方程为:

当角速度为ω时,转子的轴向移动速度v为

由式(16)、式(17)、式(18)可得转子到达回转轨道时的速度v0:

转子在运动到螺旋轴回转段,受到反向旋转力矩,带动滑套转动一定角度,很短时间内实现减速、转向和加速,转子与回转轨道的侧槽面几乎是线接触,产生较大的接触应力严重影响螺旋轴组件工作状况,其受力分析如图6所示。
根据螺旋轴运动模型,得螺旋升角α为

由于摩擦力Fμ=μmg,则滑道受到的正压力

图6 转子受力分析Fig.6 Force analysis of rotor
为:

式中,m为载秧台和连接部件总质量;μ为秧箱与底架摩擦系数;g为重力加速度。
在移箱机构运行过程中,滑道所受到的正压力一直是变化的,且由于秧箱滑块和秧箱之间的预紧力F'的不同,使得秧箱与底架摩擦系数μ也不相同,根据文献[21]将式(21)修改为:

将SolidWorks中建立的螺旋轴式移箱机构导入到Adams软件中,根据实际工作状态和受力分析情况,定义材料属性、添加运动副、施加载荷和约束、添加驱动,建立仿真模型,进行运动学仿真。经仿真分析,得到滑套质心水平运动速度曲线和转子与滑套接触力曲线,分别如图7、图8所示。
从图7、图8可知,在移箱机构运行过程中,组件之间相互碰撞摩擦会产生应力磨损,导致运行速度的不平稳,特别在换向回转阶段的过渡曲线处会有较大的冲击力,加剧了螺旋轴换向段的磨损,同时正常移动阶段滑套速度出现较大波动,相同时间内秧箱的移动距离差距较大,使得分插机构每次从秧盘中取苗数目产生较大误差,严重影响高速水稻插秧机栽插秧苗的精准性。
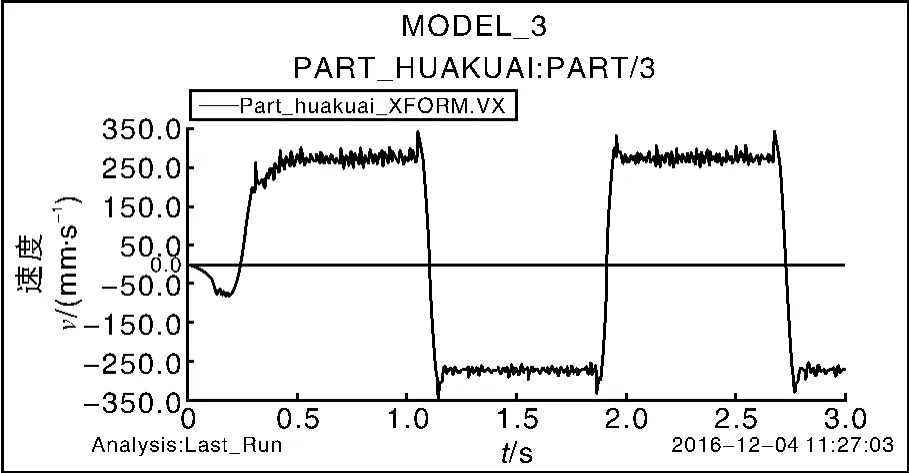
图7 滑套质心水平运动速度曲线图Fig.7 Chart of CM horizontal movement velocity of slider

图8 滑套和螺旋轴接触力曲线图Fig.8 Chart of contact force between slide and screw axis
因此,运动学性能的优化目标是滑套在过渡曲线处转速运行过程中滑套与螺旋轴的接触应力最小,使得螺旋轴式移箱机构在工作过程中速度波动减小,运行更加精准可靠。
2.3 结构力学性能分析
高速插秧机移箱机构在运行过程中需要负载秧箱和秧苗大约20 kg,其支承方式属于一端固定、一端支承的方式,由于负载的作用带给螺旋轴较大的负荷,同时转子和滑套也相应受到较大的冲击致使其承受较大的力。因此,需要将螺旋轴组件进行结构力学性能分析,并根据结构力学性能分析结果建立优化模型,以减轻其质量。
在ANSYS软件中导入建立好的螺旋轴、滑套和转子的三维模型,选用3-D固体结构单元SOLID95单元,分别定义组件材料的弹性模量和泊松比,选用自由网格划分方法进行网格划分。由于滑套只做水平往复直线运动,转子在滑套内孔旋转且随滑套水平往复,所以定义约束边界条件为滑套轮毂内孔的所有自由度全约束;最后施加载荷,建立结构力学分析模型。通过有限元计算分析得到螺旋轴、转子和滑套的应力应变分析云图,如图9所示。
因此,结构力学性能优化的目标是保证螺旋轴、转子和滑套最大应力小于许用应力的条件下,使得组件的质量最轻。
3 多学科协同设计优化
3.1 多学科优化方法的选择
本文涉及3个学科,各学科之间耦合关系较强,属于多级优化方法中的面向非层次系统。并行子空间优化方法是基于GSE的线性近似,子空间设计变量范围较窄,而且不一定能保证收敛,会出现振动现象。协同优化方法在系统级将各学科间共享的优化变量提取出来,构成系统级优化变量,对系统级优化变量和学科耦合变量进行优化,以系统级优化变量和学科耦合变量取值与各学科优化输出方案保持一致为约束条件,使得MOD问题的目标函数数值最小[22]。该方法简单易行,符合现代工程设计模式,因此,本文选择协同优化方法来构建螺旋轴式移箱机构的多学科设计优化模型。

图9 螺旋轴组件等效应力图Fig.9 Equivalent stress for screw axis components
3.2 优化变量的选择
由于移箱机构各部件设计参数繁多,对目标性能影响又不一样,如将所有设计参数都作为优化变量,会使优化周期过长,增加优化难度。为了降低优化难度和提高优化效率,通过分析各设计参数对优化目标的影响程度,确定影响优化目标的关键参数作为设计变量,从而降低优化变量空间维数[19]。采用iSIGHT软件提供的试验设计模块进行灵敏度分析,采用优化拉丁超立方设计法计算各设计参数对各优化目标的贡献度,得到计算结果的Pareto图,如图10所示。
由图10可得:不同的设计变量对每个学科优化目标的贡献程度不同,选择贡献度大于5%的设计变量作为各学科的优化变量。设计变量D、d、P、b、A、α 对模态影响程度比较大;设计变量A、r、P、α、b、θ对接触应力的影响程度比较大;H、L、T、D、d、r对质量的影响程度比较大。
3.3 螺旋轴式移箱机构协同优化数学模型建立
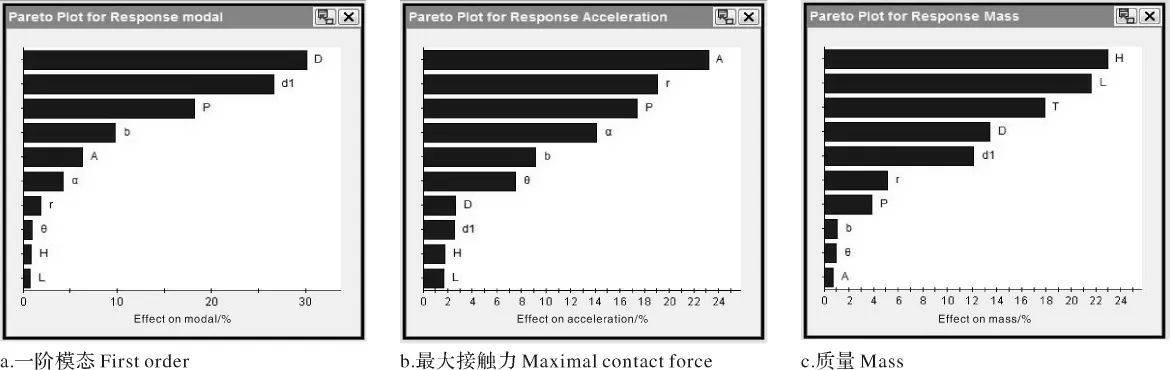
图10 设计参数对优化目标的Pareto图Fig.10 Pareto diagram of design parameters to optimization targets
螺旋轴式移箱机构多学科协同优化目标是使移箱机构的一阶模态最大,接触力和质量最小。根据协同优化方法的计算框架,建立螺旋轴式移箱机构系统级优化数学模型和各学科级优化数学模型。
基于CO的螺旋轴式移箱机构系统级优化数学模型为:

式(23)中,下标sys的变量为系统级变量,其中sys1、sys2、sys3分别指系统级传递到子学科1、2、3的变量;上标*的变量是子学科优化传递给系统级优化的变量,为上一轮迭代各子学科优化得到的最优值;下标sys的约束为系统级约束;f1为动力学学科优化目标函数,f2为运动学学科优化目标函数,f3为结构力学学科优化目标函数。
动力学学科优化数学模型为:


式(24)中,下标sys1的变量为系统级变量传递到动力学的最优值,在动力学优化中为定值。其中τT和[σ]w分别为螺旋轴切应力和弯曲应力,主要影响螺旋轴的强度性能。
运动学学科优化数学模型为:

式(25)中,下标sys2的变量为系统级变量传递到运动学的最优值,在运动学优化中为定值。
结构力学学科优化数学模型为:

式(26)中,下标sys3的变量为系统级变量传递到结构力学的最优值,在结构力学优化中为定值。其中σe是转子与滑套的最大应力,在相同材质的情况下,结构尺寸参数越大能承受的应力应变能力越强,而结构力学的目标是质量最轻,减小尺寸参数使得结构更加紧凑,因此,优化设计时应综合考虑移箱机构各组件的应力情况。
根据系统级和各学科建立的数学模型构建了总体MDO框图如图11所示,系统级优化将利用各个学科返回的解进一步使系统级设计变量最优解的约束违背程度趋近于零,这个过程不断进行,直到迭代收敛为止。
参考久保田SPV-6C型高速水稻插秧机确定相关参数[23-24],螺旋轴转速 n 为 665 r·min-1,传递效率P为1.35 kW,强度系数C为102。利用iSIGHT软件集成ANSYS Workbench和Adams等软件建立螺旋轴式移箱机构多学科协同优化平台[25],如图 12 所示。

图11 螺旋轴式移箱机构协同优化框图Fig.11 Framework map of collaborative optimization algorithm for screw axis type moving-box mechanism
根据上文SolidWorks建立的参数化模型得到各设计变量的初始值,在选用序列二次规划法作为优化算法基础上,对该多学科协同优化模型进行求解,得到的优化结果如表3所示。
从表3中可以看出,在满足各约束条件的前提下,螺旋轴的一阶模态由236.428 Hz提高到263.403 Hz,增加了11.40%,有效提升了螺旋轴的抗振性能;移箱机构工作运行时,最大接触力由479.832N减小至 421.831N,降低了12.08%,减少了应力磨损,使机构运行更加可靠,提高了机栽插秧苗精准性;转子的最大应力由9.741 MPa增加到11.830 MPa,滑套的应力由30.385 MPa增加到35.992 MPa,在保证强度性能的条件下,机构质量降低了17.77%,使得结构更加紧凑,降低了制造成本;总体上得到了较满意的优化结果。
根据优化后的设计参数重新建立优化模型分别再进行仿真分析,得到优化前后的螺旋轴一阶模态、接触力、转子和滑套应力对比图分别如图13、图14、图15、图16和图17所示。
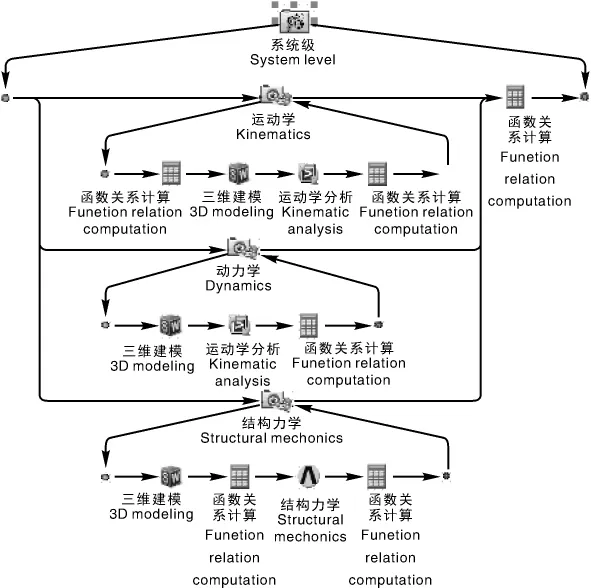
图12 螺旋轴式移箱机构MDO集成平台Fig.12 MDO integrated platform of screw axis type moving-box mechanism

图13 一阶模态优化前后对比Fig.13 First modal comparison before and after optimization
结合仿真分析图和仿真验证数据表可以看出,螺旋轴的一阶模态有所提高;在换向回转阶段转子和滑套运动到螺旋轴两端的过渡曲线处产生接触力峰值均有所降低,同时正常移动阶段的接触力均值也有较大程度的降低;转子和滑套的应力虽然有所增加但也远低于屈服强度;其分析结果与最终的优化结果也基本吻合,进一步验证了协同优化的可靠性。
4 结论
(1)基于多学科设计优化理论,选择螺旋轴一阶模态、机构接触力和质量作为优化设计目标,将螺旋轴式移箱机构的设计优化分解为以动力学、运动学和结构力学三个学科为基础的模型,并分别进行了学科级和系统级分析。

图14 接触力曲线优化前后对比Fig.14 Contact force comparison before and after optimization

图15 螺旋轴等效应力优化前后对比图Fig.15 Equivalent stress of screw axis comparison before and after optimization

图16 转子等效应力前后对比图Fig.16 Equivalent stress of rotor comparison before and after optimization

图17 滑套等效应力前后对比图Fig.17 Equivalent stress of sliding sleeve comparison before and after optimization
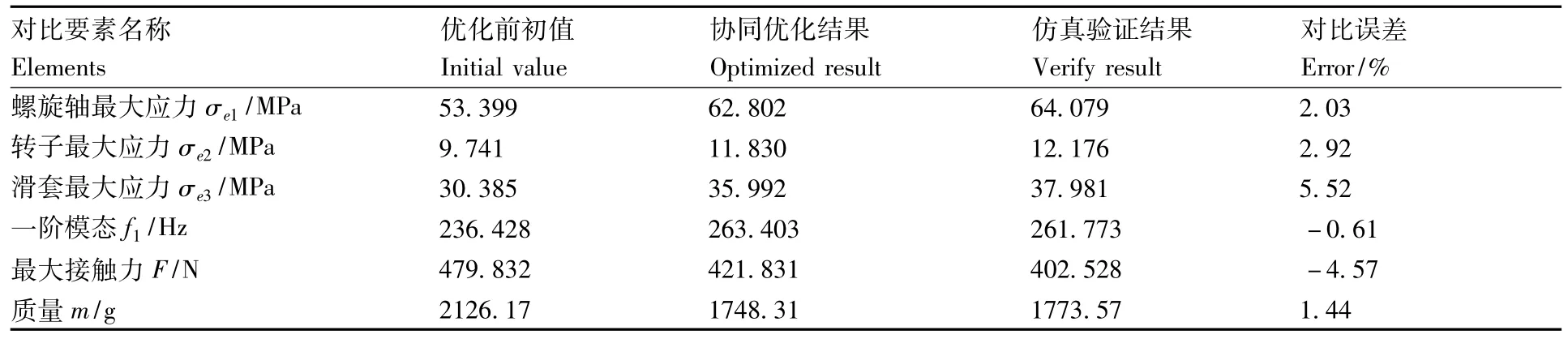
表4 仿真验证结果Table 4 Verification results of simulation
(2)基于试验设计(DOE)方法,对螺旋轴式移箱机构各设计参数进行Pareto分析,得到对各学科贡献度大的设计参数作为设计变量,有效减少计算时间,降低优化成本。同时,经过分析对比,基于协同优化方法(CO)建立了螺旋轴式移箱机构协同优化的数学模型。
(3)基于仿真分析和iSIGHT集成优化平台,利用协同优化方法和序列二次规划算法,在满足约束的前提下实现了螺旋轴移箱机构的动力学、运动学和结构力学多个学科全局优化,其优化结果兼顾了机构的振动较小、接触力较小和质量较轻,有效提高了移箱机构的整体性能。
